Mag0304_3.DOC 18 11/11/2003 Bedeutung: Das

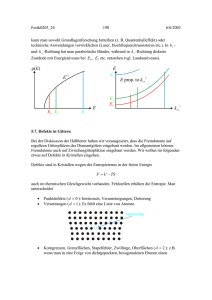
Mag0304_3.DOC
18
11/11/2003
Bedeutung: Das magnetische Moment ändert sich in einer Richtung die senkrecht zu µ
und B steht. Es präzediert um B mit der Larmorfrequenz
ω L = γB .
µ richtet sich nicht parallel zu B aus (wie in einem Motor). Die Länge von µ ändert sich
nicht. Dies bedeutet auch, dass sich die potentielle Energie
E = −µ ⋅ B
in Funktion der Zeit nicht ändert (siehe Übungsaufgabe).
Für die potentielle Energie zweier wechselwirkender Dipole erhält man
E=−
1  3(µ1 ⋅ r) (µ 2 ⋅ r ) µ1 ⋅ µ 2 
−

.
4π 
r5
r3 
Aufgrund dieser Gleichung ist unmittelbar klar, dass mit Hilfe von Spin-behafteten
Teilchen (Photonen, Müonen, Neutronen, Elektronen, etc.) magnetische Phänomene
untersucht werden können. In der Neutronenstreuung folgt aus der Vektorabhängigkeit
der Dipol-Dipol Wechselwirkung, dass nur magnetische Fluktuationen senkrecht zum
Streuvektor beitragen.
Der Vollständigkeit halber notieren wir noch folgende wichtigen Gleichungen:
Elektromagnetische Kraft auf geladenes Teilchen: F = qE + q ( v × B )
Kraft eines inhomogenen Magnetfelds auf Dipol: F = ∇(µ ⋅ B ) .
1.3.3. Demagnetisierungseffekte
Bringt man ein magnetisches Material in eine Magnetfeld, ändern sich sowohl die
magnetischen Felder innerhalb und ausserhalb des Materials. Wir wollen nicht in Details
gehen (siehe zum Beispiel J. D. Jackson, p. 192 ff).
Betrachte einen Raum ohne Material, dann gilt:
B a = µ0 Ha .
Bringt man jetzt Material in die Region, dann betragen die Felder im Material. Im
Spezialfall eines Ellipsoids sind die Felder unabhängig vom Ort, falls das Magnetfeld
entlang einer Hauptachse angelegt wird. Wir beschränken uns auf diesen Spezialfall (für
Mag0304_3.DOC
19
11/11/2003
die Berechnung von Demagnetisierungsfaktoren für Quader siehe: A. Aharoni, J. Appl.
Phys. 83, 3432 (1998); 87, 6564 (2000)). Dann gilt:
H i = H a − NM
B i = µ 0 ( H i + M ) = µ 0 (H a − N M + M ) = B a + µ 0 (1 − N ) M .
B-Feld
(quellenfrei)
H-Feld
Die Figur zeigt das Feld einer homogen magnetisierten Kugel im feldfreien Raum.
Den Ausdruck H d = − N M bezeichnet man als Demagnetisierungsfeld, es wirkt dem
äusseren Feld entgegen. Beachte: N x + N y + N z = 1 .
Einige wichtige Beispiele für die Neutronenstreuung (siehe Blundell p. 214):
a) Kugel: N x = N y = N z = 13 :
H i = H a − 13 M
B i = B a + 23 µ 0 M
b) Nadel: N x = N y = 12 , N z = 0 :
H ix = H iy = H a − 12 M , H iz = H az
Bix = B iy = Ba + 12 µ 0 M , Biz = B az
c) Platte: N x = N y = 0, N z = 1 :
H ix = H iy = H a , H iz = H az − M
Bix = Biy = B a + µ 0 M , Biz = Baz
Für Demagnetisierungsfaktoren für Rotationsellipsoide siehe A. M. Morrish, John Wiley
& Sons Inc., New York, 1965, p. 645.
Die obigen Beziehungen gelten nur, wenn keine Domänenbildung auftritt! Vergleicht
man gemessene Suszeptibilitäten, χ exp , mit berechneten, χ theo , dann gilt:
Mag0304_3.DOC
20
χ exp =
11/11/2003
M / Hi
χi
M
M
=
=
=
.
H a H i + NM 1 + NM / H i 1 + N χ i
Vorsicht: Bei einem isotropen Ferromagneten werden normalerweise zuerst die
Domänen ausgerichtet. Solange er nicht homogen magnetisiert ist, ist das H-Feld im
Innern kleiner als das angelegte Feld H a und das Zeemangap gµ B ∑ S j ⋅ B ist erst voll
ausgebildet, wenn H a > NM wird (siehe P. Böni et al., Phys. Rev. B 52, 10142 (1995)).
1.3.4. Wellenlängenabhängige Suszeptibilität
Die Beziehung zwischen den Grössen D und E sowie H und B ist nicht lokal. Dies ist
unmittelbar klar aus folgendem Grund: Die elektronischen Niveaus in einem Festkörper
unterscheiden sich von denjenigen in freien Atomen wegen dem Überlapp der
Wellenfunktionen. Die Eigenschaften der Elektronen sind also bestimmt durch die
Gesamtheit der Elektronen. Im Extremfall der freien Elektronen ist die Wechselwirkung
vollkommen delokalisiert.
Aus diesem Grund hat die Beziehung zwischen M und H die folgende Form (es ist eine
Faltung):
M α (r, t ) =
∑ ∫ d r ' ∫ dt ' χ
3
β = x, y , z
Mit Hilfe der Fouriertransformation
αβ
(r' , t ' ) H β (r − r' , t − t' ) .
f (Q ,ω ) = ∫ d 3 r ∫ dt ∫ f (r, t )e − i (Q ⋅r−ωt ) erhält man
die einfache Beziehung
M α (Q, ω ) =
∑
β = x, y , z
χ αβ (Q, ω ) H β (Q, ω ) .
Die wellenlängenabhängige Suszeptibilität χαβ (Q, ω ) ist die zentrale Grösse, die uns im
folgenden Beschäftigen wird.
In einem typischen Neutronenstreuexperiment legen wir mit Hilfe der Neutronen eine
harmonisches Feld H (Q, ω ) an und erhalten durch Messung der Streufunktion
Sαβ (Q, ω ) =< n + 1 > Im χ αβ (Q ,ω ) die Magnetisierung M (Q, ω ) in der Probe auf einer
atomaren Skala und für typische Frequenzen von THz.
•
•
Antiferromagnet: Die Richtung der Magnetisierung ändert sich von einer
Atomposition zur nächsten: 2π / q ≅ a (a ist die Gitterkonstante).
Spinwellen: Die Impulsänderung des Neutrons p = hk muss dem Impuls der
erzeugten oder vernichteten Anregung entsprechen.
Mag0304_3.DOC
21
11/11/2003
Bemerkung: Die Suszeptibilität χ = M / H ist eine dimensionslose Grösse, sie gibt an,
wieviele magnetische Momente pro Volumeneinheit durch H induziert werden. Oft wird
in den Tabellen die molare Suszeptibilität (m3 mol-1 ) angegeben:
χ m = χVm ,
wobei Vm das Volumen eines Mols der Substanz bezeichnet. Beispiel für Kupfer
(diamagnetisch, N A = 6.022 ⋅10 23 mol -1 , Volumen pro Atom:VEZ = 1.18 ⋅10 −29 m 3 ):
χ = −1.1 ⋅10 −6
⇒
χ m = N AV EZ χ = −7.8 ⋅10 −12 m 3 / mol .
Oft wird auch die Massensuszeptibilität (m3 kg-1 ) angegeben: χ g =
χ
ρ
Für eine Diskussion der magnetischen Felder H und B siehe J. Crangle and M. Gibbs,
Physics World, November 1994, p. 31. Ich vertrete die Ansicht der meisten
Leserbriefschreiber dazu, dass man das H-Feld unbedingt beibehalten sollte und nicht
durch B0 = µ 0 H ersetzen sollte.
Beachte auch die Transformation der folgenden Einheiten:
Item
B
H
χ
E
Energie-Produkt
SI-Einheit
1 T = 1 Vsm-2
1 Am-1 = 1 JT-1 m-3
1 JT-2 kg-1
1J
1 kJm-3
cgs-Einheit
104 G
4π⋅10-3 Oe
10-6 ergOe-1g-1 = 10-6 emu g-1
107 erg
0.1256 MG Oe = 104 ergcm-3
1.3.5. Diamagnetismus: Klassische Behandlung
Der Diamagnetismus kann mit Hilfe der Lenz’schen Regel erklärt werden:
Induktionsströme sind so gerichtet, dass sie der Flussänderung entgegenwirken.
B
I
M
Dadurch wird das äussere Feld abgeschirmt (vgl. Supraleiter). Das angelegte B Feld wird
reduziert: µ < 1 ⇔ χ dia < 0 . Reine Diamagnete sind Systeme bei denen der