5 Das Haus der Vierecke

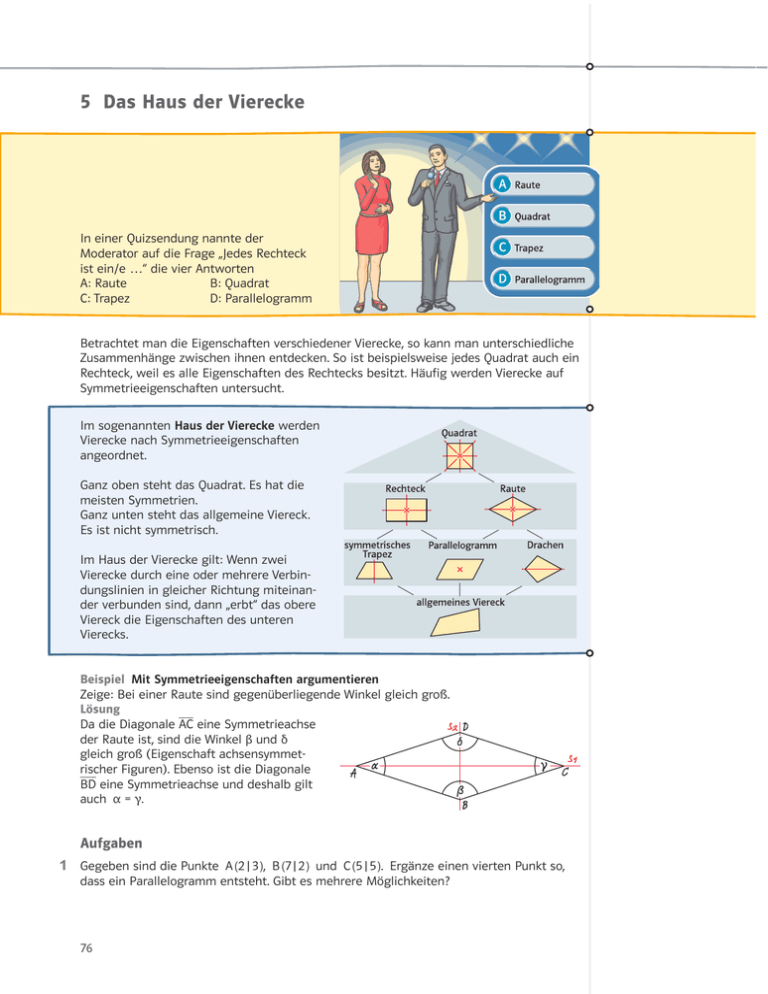
5 Das Haus der Vierecke
In einer Quizsendung nannte der
Moderator auf die Frage „Jedes Rechteck
ist ein/e …“ die vier Antworten
A: Raute
B: Quadrat
C: Trapez
D: Parallelogramm
Betrachtet man die Eigenschaften verschiedener Vierecke, so kann man unterschiedliche
Zusammenhänge zwischen ihnen entdecken. So ist beispielsweise jedes Quadrat auch ein
Rechteck, weil es alle Eigenschaften des Rechtecks besitzt. Häufig werden Vierecke auf
Symmetrieeigenschaften untersucht.
Im sogenannten Haus der Vierecke werden
Vierecke nach Symmetrieeigenschaften
angeordnet.
Ganz oben steht das Quadrat. Es hat die
meisten Symmetrien.
Ganz unten steht das allgemeine Viereck.
Es ist nicht symmetrisch.
Im Haus der Vierecke gilt: Wenn zwei
Vierecke durch eine oder mehrere Verbindungslinien in gleicher Richtung miteinander verbunden sind, dann „erbt“ das obere
Viereck die Eigenschaften des unteren
Vierecks.
Beispiel Mit Symmetrieeigenschaften argumentieren
Zeige: Bei einer Raute sind gegenüberliegende Winkel gleich groß.
Lösung
__
Da die Diagonale AC eine Symmetrieachse
der Raute ist, sind die Winkel β und δ
gleich groß (Eigenschaft achsensymmetrischer
Figuren). Ebenso ist die Diagonale
___
BD eine Symmetrieachse und deshalb gilt
auch α = γ.
Aufgaben
1 Gegeben sind die Punkte A (2 | 3 ), B (7 | 2 ) und C (5 | 5 ). Ergänze einen vierten Punkt so,
dass ein Parallelogramm entsteht. Gibt es mehrere Möglichkeiten?
76
2 In Fig. 1 ist das Rechteck KMOJ enthalten.
Man muss schon genauer hinsehen, um
das Drachenviereck EFND zu entdecken.
Suche möglichst viele weitere besondere
Vierecke.
3 In welchen Vierecken halbiert jede der
zwei Diagonalen die andere? Gibt es auch
Vierecke, bei denen nur eine der zwei Diagonalen die andere halbiert?
4 a) Konstruiere die folgenen Vierecke:
Quadrat: a = 6 cm
Rechteck: a = 6 cm; b = 4 cm
Raute: a = 6 cm; β = 70°
Parallelogramm: a = 6 cm; b = 4 cm;
β = 70°
symmetrisches Trapez: a = 6 cm; b = 4 cm;
β = 70°
Drachen: a = 6 cm; b = 4 cm; β = 70°
b) Ordne die gezeichneten Vierecke nach
zwei verschiedenen, selbst gewählten
Eigenschaften.
Fig. 1
5 Lege auch für die anderen symmetrischen
Vierecke Steckbriefe nach dem Vorbild von
Fig. 2 an.
Fig. 2
6 Aus den Plättchen kann man verschiedene Arten von symmetrischen Vierecken zusam-
Interaktives Üben
Symmetrische
Vierecke
674bz7
mensetzen. Du darfst dabei auch mehrere Plättchen einer Sorte und Plättchen von verschiedenen Sorten verwenden. Skizziere fünf Beispiele so zusammengesetzter Vierecke.
D
7 Zeichne mit den gegebenen Stücken einen Drachen ABCD. Bestimme aus der Zeichnung
A
H
C
die Größen der fehlenden Seiten und Winkel. Die Diagonalen sind mit e und f bezeichnet.
a) b = 1,5 cm, d = 4 cm, γ = 80°
b) α = 50°, e = 5,5 cm, f = 4 cm
c) a = 3 cm, α = 35°, β = 135°
d) d = 3,5 cm, γ = 60°, f = 2 cm
8 Untersuche, ob es sich um einen Drachen handelt. Begründe.
a)
b)
c)
d)
5 Das Haus der Vierecke
I
B
77