I/A Ma 1

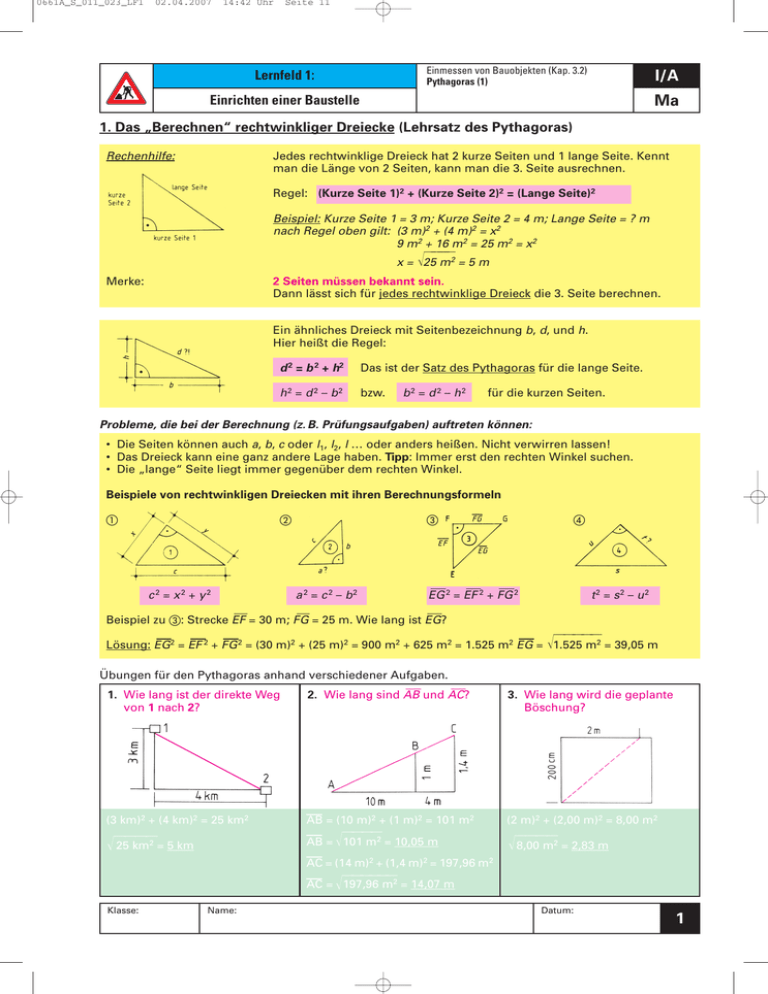
0661A_S_011_023_LF1
02.04.2007
14:42 Uhr
Seite 11
Einmessen von Bauobjekten (Kap. 3.2)
Pythagoras (1)
Lernfeld 1:
I/A
Ma
Einrichten einer Baustelle
1. Das „Berechnen“ rechtwinkliger Dreiecke (Lehrsatz des Pythagoras)
Rechenhilfe:
Jedes rechtwinklige Dreieck hat 2 kurze Seiten und 1 lange Seite. Kennt
man die Länge von 2 Seiten, kann man die 3. Seite ausrechnen.
Regel: (Kurze Seite 1)2 + (Kurze Seite 2)2 = (Lange Seite)2
Beispiel: Kurze Seite 1 = 3 m; Kurze Seite 2 = 4 m; Lange Seite = ? m
nach Regel oben gilt: (3 m)2 + (4 m)2 = x2
9 m2 + 16 m2 = 25 m2 = x2
苶苶苶
苶2 = 5 m
x = 冑25
m
Merke:
2 Seiten müssen bekannt sein.
Dann lässt sich für jedes rechtwinklige Dreieck die 3. Seite berechnen.
Ein ähnliches Dreieck mit Seitenbezeichnung b, d, und h.
Hier heißt die Regel:
d 2 = b 2 + h2
Das ist der Satz des Pythagoras für die lange Seite.
h2 = d 2 – b2
bzw.
b2 = d 2 – h2
für die kurzen Seiten.
Probleme, die bei der Berechnung (z. B. Prüfungsaufgaben) auftreten können:
• Die Seiten können auch a, b, c oder l1, l2, l … oder anders heißen. Nicht verwirren lassen!
• Das Dreieck kann eine ganz andere Lage haben. Tipp: Immer erst den rechten Winkel suchen.
• Die „lange“ Seite liegt immer gegenüber dem rechten Winkel.
Beispiele von rechtwinkligen Dreiecken mit ihren Berechnungsformeln
햲
햳
c2 = x2 + y2
햴
a 2 = c 2 – b2
햵
EG 2 = EF 2 + FG 2
t2 = s2 – u2
Beispiel zu 햴: Strecke EF = 30 m; FG = 25 m. Wie lang ist EG?
苶苶苶苶
苶2 = 39,05 m
Lösung: EG2 = EF 2 + FG 2 = (30 m)2 + (25 m)2 = 900 m2 + 625 m2 = 1.525 m2 EG = 冑1.525
m
Übungen für den Pythagoras anhand verschiedener Aufgaben.
1. Wie lang ist der direkte Weg
von 1 nach 2?
2. Wie lang sind AB und AC?
3. Wie lang wird die geplante
Böschung?
(3 km)2 + (4 km)2 = 25 km2
AB = (10 m)2 + (1 m)2 = 101 m2
(2 m)2 + (2,00 m)2 = 8,00 m2
冑苶苶苶苶
25 km2 = 5 km
AB = 冑苶苶苶苶
101 m2 = 10,05 m
冑苶苶苶苶
8,00 m2 = 2,83 m
AC = (14 m)2 + (1,4 m)2 = 197,96 m2
苶苶苶
苶2 = 14,07 m
AC = 冑苶苶
197,96
m
Klasse:
Name:
Datum:
1
0661A_S_011_023_LF1
31.03.2007
13:06 Uhr
Seite 12
Einmessen von Bauobjekten (Kap. 3.2)
Pythagoras (2)
Lernfeld 1:
A
Ma
Einrichten einer Baustelle
4. Wie lang ist die schräge Seite?
5. Besser misst man immer gleich
in der gesuchten Einheit. Das
geschah hier nicht.
6. Wie kann man kontrollieren,
dass A richtig eingemessen
wurde?
5,22 m
8,42 m
Verbindung: 14,4 m
Letzte Aufgabe: Wie groß ist y ? (z = 12,4 m, x = 8,9 m)
8,63 m
2. Das Seitenverhältnis 3 : 4 : 5
Sollen auf der Baustelle rechte Winkel abgetragen werden, wird vorwiegend eine Erkenntnis aus dem
„Pythagoras“ verwendet:
Rechenhilfe:
Bauteilabsteckung
Beispiele:
Mauerecke
Wenn das Seitenverhältnis
3:4:5
beträgt, entsteht automatisch
ein rechter Winkel.
Beispiele:
3 x (1 m) : 4 x (1 m) : 5 x (1 m)
Grundgröße ist 1 m
oder:
3 x (40 cm) : 4 x (40 cm) : 5 x (40 cm)
Grundgröße ist 40 cm
Messband
Aufgabe: Gegeben ist die Grundgröße. Wie groß müssen
die anderen Seiten sein, damit ein rechter Winkel entsteht?
Bauwinkel
Aufgabe: Bestimmen Sie für einen Bauwinkel die restlichen Seitenlängen.
Grundgröße
L1
L2
L3
a (= 3 x …)
b (= 4x …)
c (= 5 x …)
20 cm
60 cm
80 cm
1,00 m
15 cm
20 cm
25 cm
50 cm
1,50 m
2,00 m
2,50 m
18 cm
24 cm
30 cm
60 cm
1,80 m
2,40 m
3,00 m
48 cm
64 cm
80 cm
1,2 m
3,60 m
4,80 m
6,00 m
45 cm
60 cm
75 cm
1,5 m
4,50 m
6,00 m
7,50 m
1,05 m
1,40 m
1,75 m
Aufgabe: Wie lang sind die beiden anderen Seiten, wenn die kürzeste Seite eines Dreiecks 2,10 m beträgt?
Grundgröße2,10 m = 0,70 m; Mittlere Seite: (4 x 0,70m) = 2,80 m; Längste Seite: (5 x 0,70m) = 3,50 m
Grundgröße: ––––––– = 0,70 m; Mittlere Seite: (4 x 0,70 m) = 2,80 m; Längste Seite: (5 x 0,70 m) = 3,50 m
Grundgröe: 3 = 0,70 m; Mittlere Seite: (4 x 0,70m) = 2,80 m; Längste Seite: (5 x 0,70m) = 3,50 m
Klasse:
Name:
Datum:
2