Einblick - Europa

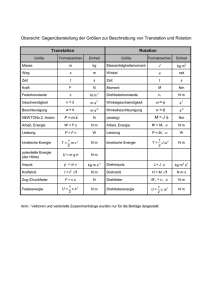
Ba
87,62
56
Sr
40,078
38
Ca
226,025
Ra*
(227)
Ac*
138,9055
89
La
88,90585
57
Y
44,95591
39
Sc
21
3
III B
Ta
(261)
W
(263)
Rf*
Fe
26
8
Re
(99)
75
Tc*
Os
101,07
76
Ru
54,93805 55,845
43
44
Mn
25
7
VII B
Nd
60
(262)
Bh*
Pd
58,6934
46
Ni
28
10
Ir
Pt
102,9055 106,42
77
78
Rh
58,9332
45
Co
27
9
VIII B
Pa*
Th*
U*
62
(266)
94
150,36
Np* Pu*
93
(145)
Pm* Sm
61
(265)
Hn* Mt*
Hg
96
157,25
Gd
64
(243)
(247)
Si
12,011
14
C
6
14
IV A
Pb
118,710
82
Sn
72,61
50
Ge
O
8
16
VI A
S
Se
Po*
127,60
84
Te
208,9804 (209)
115
116
Bi
121,757
83
Sb
74,92159 78,96
51
52
As
30,97376 32,066
33
34
P
14,00674 15,9994
15
16
N
7
15
VA
(277)
(287)
Dy
66
97
(247)
(251)
Cf*
98
158,9253 162,50
Tb
65
Er
68
(288)
(252)
Es*
99
101
Element 105: Ha (Hahnium)
Element 106: Sg (Seaborgium)
Xe
83,80
54
Kr
39,948
36
Ar
Yb
70
(210)
At*
102
103
174,967
Lu
71
(293)
Uuo*
(222)
116
Rn*
126,9045 131,29
85
86
I
79,904
53
Br
35,4527
35
CI
168,9342 173,04
Tm
69
(289)
Ne
4,002602
10
18,99840 20,1797
17
18
F
9
17 2
VII A He
18
VIII A
(257)
(258)
(259)
Element 107: Ns (Nielsbohrium)
(260)
Fm* Md* No* Lr*
100
164,9303 167,26
Ho
67
(289)
Cn* Uut* Uuq* Uup* Uuh*
204,3833 207,20
113
114
TI
114,82
81
In
69,723
49
Ga
26,98154 28,0855
31
32
AI
Superschwere Elemente
(272)
Rg*
196,9665 200,59
111
112
Au
Am* Cm* Bk*
95
151,965
Eu
63
(269)
Ds*
Cd
65,39
48
Zn
30
12
II B
107,8682 112,411
79
80
Ag
63,546
47
Cu
29
11
IB
10,811
13
B
5
13
III A
Hauptgruppen
Die Bezeichnungen der Elemente 104 … 109 entsprechen der vorläufigen IUPAC-Empfehlung. Abweichend davon werden folgende Bezeichnungen verwendet:
232,0381 231,0359 238,0289 237,0482 (244)
91
90
92
140,9077 144,24
Pr
59
Actinoiden
140,115
Ce
58
Lanthanoiden
(262)
Db* Jl*
Element 104: Ku (Kurtschatovium) oder Rf (Rutherfordium)
Element 108: Hs (Hassium)
1)
Mo
51,9961
42
Cr
24
6
VI B
92,90638 95,94
73
74
Nb
50,9415
41
V
23
5
VB
Nebengruppen
178,49
180,9479 183,84
186,207 190,2
192,22
195,08
104
1) 105
1) 106
1) 107
1) 108
1) 109
1) 110
Hf
91,224
72
Zr
47,87
40
Ti
22
4
IV B
Dunkelrot: Unter Normbedingungen flüssig
Hellrot:
Unter Normbedingungen gasförmig
Relative Atommasse
(Klammer: stabilstes
Isotop)
Elementsymbol (kursiv:
künstliches Element)
Alle Nuklide radioaktiv
Ordnungszahl
(223)
7 Fr*
132,9054 137,33
87
88
6 Cs
85,4678
55
5 Rb
39,0983
37
4 K
Pu*
Mg
9,012182
12
Be
4
22,98977 24,3050
19
20
3 Na
6,941
11
2 Li
1,00794
3
2
II A
Die Gruppennummer der Hauptgruppe entspricht der Anzahl der Außenelektronen,
die Periodennummer entspricht der Anzahl der Hauptenergieniveaus bzw. der Anzahl
der Elektronenschalen nach Bohr.
08:09
(244)
1
1 H
1
IA
Hauptgruppen
Periodensystem der Elemente
21.10.13
94
Perioden
00 (001-004)_ TB San 001-014
Seite U 2
00 (001-004)_ TB San 001-014
21.10.13
08:09
Seite 1
E U R O PA - F A C H B U C H R E I H E
für metalltechnische Berufe
Grundlagen
Technische
Physik
Tabellenbuch
Technische
Kommunikation
Wärme ● Kälte ● Klima
Stoffkunde
Fertigungstechnik
6. überarbeitete Auflage
Klimatechnik
Kältetechnik
VERLAG EUROPA-LEHRMITTEL · Nourney, Vollmer GmbH & Co. KG
Düsselberger Straße 23 · 42781 Haan-Gruiten
Europa-Nr.: 1731X
Allgemeine
Anlagentechnik
00 (001-004)_ TB San 001-014
21.10.13
08:09
Seite 2
Autor und Leiter des Arbeitskreises:
Martin Tonert
Oberstudienrat
Co-Autoren:
Ewald Bach
Peter Bertrand
Dipl.-Ing. Walter Bierwerth
Dipl.-Ing. Horst Herr
Oberstudienrat
Studienrat
Studiendirektor
Fachoberlehrer VDI, DKV
Umschlaggestaltung:
Petra Gladis-Toribio, Kelkheim
Bildbearbeitung:
Michael M. Kappenstein
Zeichenbüro des Verlages Europa-Lehrmittel, Ostfildern
In diesem Tabellenbuch wurden die neuesten Ausgaben der DIN-Normen und der sonstigen Regelwerke zugrunde gelegt. Es wird jedoch darauf hingewiesen, dass nur die DIN-Normen selbst verbindlich sind. Diese können in den öffentlichen DIN-Normen-Auslegestellen eingesehen oder
durch die Beuth Verlag GmbH, Burggrafenstraße 6, 10787 Berlin, bezogen werden.
Obwohl die DIN-Normen mit großer Sorgfalt recherchiert wurden, können Autoren und Verlag
keinerlei Gewährleistung übernehmen.
Bei anderen in diesem Tabellenbuch genutzten technischen Regelwerken gilt dies sinngemäß.
6. Auflage 2013
Druck 5 4 3 2 1
Alle Drucke dieser Auflage sind im Unterricht nebeneinander einsetzbar, da sie bis auf die Behebung
der Druckfehler unverändert sind.
ISBN 978-3-8085-1736-9
Alle Rechte vorbehalten. Das Werk ist urheberrechtlich geschützt. Jede Verwertung außerhalb der
gesetzlich geregelten Fälle muss vom Verlag schriftlich genehmigt werden.
© 2013 by Verlag Europa-Lehrmittel, Nourney, Vollmer GmbH & Co. KG, 42781 Haan-Gruiten
http://www.europa-lehrmittel.de
Satz: rkt, 42799 Leichlingen, www.rktypo.com
Druck: M. P. Media-Print Informationstechnologie GmbH, 33100 Paderborn
00 (001-004)_ TB San 001-014
21.10.13
08:09
Seite 3
Vorwort
3
Die Summe unserer Erkenntnis besteht aus dem,
was wir gelernt, und dem, was wir vergessen haben.
Marie von Ebner-Eschenbach
Die Zusammenhänge zwischen den berechenbaren und messbaren Größen in Naturwissenschaft
und Technik werden fast immer in ihrer kürzesten Ausdrucksweise, durch Formeln, repräsentiert.
Somit liegt es auf der Hand, diese in Formelsammlungen zusammenzustellen, denn wegen der
großen Anzahl der notwendigen Informationen ist es unmöglich, jede in einem bestimmten Fachgebiet benötigte Formel abrufbereit im Kopf zu haben. Das diesem Vorwort vorangestellte Motto
von Marie von Ebner-Eschenbach unterstreicht dies sehr deutlich.
Neben den vielfältigen Formeln werden in jedem technischen Fachgebiet auch umfangreiche
Tabellen, oft auch in der Form von DIN-Blättern und sonstigen technischen Regeln, benötigt. In
allen technischen Hauptrichtungen – wie etwa im Maschinenbau, der Elektrotechnik oder der Bautechnik – gehört es seit langem zur guten Tradition, die benötigten Formeln und Tabellen in einem
Tabellenbuch zusammenzufassen. Hauptorientierungsmerkmale sind dabei die entsprechenden
Verordnungen über die Berufsausbildung sowie die Lehrpläne für die Meister- und Technikerausbildung. Diese Lücke schließt das
Tabellenbuch Wärme • Kälte • Klima
Orientierungsgrundlagen waren dabei vor allem die Verordnungen über die Berufsausbildung,
und zwar für Mechatroniker für Kältetechnik und Anlagenmechaniker SHK. Die Lerninhalte der
beruflichen Erstausbildung wurden durch solche der Meister- und Technikerausbildung ergänzt.
Von vornherein war also beabsichtigt, ganze Berufsfelder und nicht nur deren Kernbereich zu erfassen. Des Weiteren wurde versucht – dem Buchtitel gemäß – mehrere Berufsfelder zu verbinden.
Damit wurde auch dem Trend in Richtung Universalität der Berufsausübung bzw. Berufsausbildung Rechnung getragen.
Bei der Festlegung der Buchinhalte wurde also strikt darauf geachtet, dass auch das „was man
sonst noch braucht“ seinen Platz gefunden hat. Exemplarisch sind hier die Mathematik, die
Technische Kommunikation, die Stoffkunde und die Fertigungstechnik zu nennen. Im Bereich der
Technischen Physik sind bereits viele Lehrinhalte aus der Anlagentechnik enthalten bzw. solche
Lehrinhalte, die in der Anlagentechnik vorausgesetzt werden. Mit den acht Hauptabschnitten
(s. Seite 4) wird zwar eine grobe Gliederung der Lehrinhalte erreicht, manche Themenbereiche sind
jedoch dort eingegliedert, wo man sie bei der praktischen Anwendung sucht.
Die große Stofffülle bringt es mit sich, dass die Erforderlichkeit einiger Themenbereiche sicherlich
umstritten bleibt. Vielleicht werden aber auch andere Themenbereiche vermisst oder als unterrepräsentiert empfunden. Wie sich dieses Buch in seinen späteren Auflagen entwickelt, wird ganz
wesentlich durch die Reaktionen der Leser und Fachkollegen – worum wir ausdrücklich bitten –
beeinflusst.
In der vorliegenden 6. Auflage wurden die zitierten Normen aktualisiert und notwendige
Änderungen und Ergänzungen vorgenommen.
Wir danken allen, die durch Hinweise und Vorschläge zur weiteren Verbesserung des Tabellenbuches beigetragen haben.
Hinweise und Verbesserungsvorschläge können dem Verlag und damit den Autoren unter
[email protected] übermittelt werden.
Herbst 2013
Das Autorenteam
00 (001-004)_ TB San 001-014
21.10.13
4
08:09
Seite 4
Vorspann
Hinweise zur Arbeit mit diesem Tabellenbuch
Das Tabellenbuch ist in 8 Hauptabschnitte eingeteilt, und zwar
1
Grundlagen
GR
5
Fertigungstechnik
FT
2
Technische Physik
TP
6
Klimatechnik
KL
3
Technische Kommunikation
TK
7
Kältetechnik
KT
4
Stoffkunde
SK
8
Allgemeine Anlagentechnik
AT
Die 8 Hauptabschnitte sind deutlich durch das praktische Daumenregister voneinander getrennt.
Hauptabschnitt 8 „Allgemeine Anlagentechnik" ist nochmals in 11 Unterabschnitte durch angedeutete Tabs
unterteilt.
Am Anfang dieser Hauptabschnitte befindet sich jeweils ein ausführliches Inhaltsverzeichnis. Daraus ist zu
ersehen, dass die Hauptabschnitte nochmals in Unterabschnitte unterteilt sind.
Aus den Unterabschnitten sind die Themenüberschriften mit den entsprechenden Seitenzahlen zu ersehen.
Der Wert eines Fachbuches hängt auch sehr stark vom Umfang des Sachwortverzeichnisses ab. Hierauf wurde
ein besonderer Wert gelegt. Das Sachwortverzeichnis dieses Tabellenbuches enthält über 1900 Begriffe.
Es ist ganz normal, dass in einem Fachbuch zum gleichen Begriff an mehreren Stellen Aussagen gemacht
werden. Dies geht aus den Seitenzahlen im Sachwortverzeichnis hervor.
Orientieren Sie sich in diesem Tabellenbuch vor
allem mit Hilfe des Sachwortverzeichnisses.
Eine Besonderheit dieses Tabellenbuches besteht
jedoch darin, dass durch rote Hinweispfeile (➞) die
Sachverhalte miteinander verkettet wurden. Die Hinweispfeile zeigen Ihnen also, wo Sie noch weitere
Informationen zu der von Ihnen gewünschten Formel, Tabelle oder zu einem gewünschten Begriff finden können.
Ein roter Pfeil (➞) zeigt an, dass Sie dort noch weitere Informationen finden.
Das Tabellenbuch Wärme • Kälte • Klima
wurde von Herrn Dipl.-Ing. Horst Herr –
initiiert durch seine langjährige Tätigkeit an
der Bundesfachschule Kälte-Klima-Technik
in Maintal – realisiert.
Symbol für die globale Erwärmung:
Erdball und Heizthermostat
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
1 Grundlagen
Seite 5
GR
1.1 Allgemeine Grundlagen
5
Griechisches Alphabet
6
Römische Ziffern
6
Basisgrößen und Basiseinheiten
6
Vorsätze vor Einheiten
7
Formelzeichen und Einheiten
7
1.2 Allgemeine Mathematik
Grundrechenarten
15
15
Klammerrechnung (Rechnen mit Summen)
17
Bruchrechnung
18
Prozentrechnung
18
Potenzrechnung
19
Radizieren
20
Logarithmieren
20
Gleichungen
21
Runden von Zahlen
23
Interpolieren
23
Statistische Auswertung
24
Flächenberechnung
26
Körperberechnung
27
Geometrische Grundkenntnisse
29
Sätze der Geometrie
30
Trigonometrie
31
1.3 Technische Mathematik
33
Teilung von Längen (Gitterteilung)
33
Teilung auf dem Lochkreis
33
Rohlängen von Pressteilen (Schmiedelänge)
33
Gestreckte Längen (kreisförmig gebogen)
34
Zusammengesetzte Längen und zusammengesetzte Flächen
34
Berechnung der Masse bei Halbzeugen
34
Volumeninhalt und Oberfläche wichtiger Behälterböden
35
Inhalt unregelmäßiger Flächen
35
Diagramme und Nomogramme
36
Sonnenuntergang
mit Windrad
5
01 (005 - 039)_ TB San 015-046 GR
6
GR
21.10.13
08:11
Seite 6
1.1 Allgemeine Grundlagen
Griechisches Alphabet
Großbuchstabe
Kleinbuchstabe
Bedeutung
Name
Großbuchstabe
Kleinbuchstabe
Bedeutung
Name
Å
‹
å
a
Alpha
›
~
n
Ny
∫
b
Beta
Ù
≈
x
Xi
Ì
©
g
Gamma
Ø
ø
o
Omikron
¤
∂
d
Delta
∏
π
p
Pi
‰
™
e
Epsilon
¸
®
rh
Rho
Sigma
ˇ
Ω
z
Zeta
Í
‚
s
Ó
ª
e
Eta
˝
†
t
Tau
ı
«
th
Theta
Á
¨
y
Ypsilon
Û
⁄
i
Jota
Ï
ƒ
ph
Phi
ˆ
Δ
k
Kappa
Ç
ç
ch
Chi
fl
¬
l
Lambda
‡
¥
ps
Psi
˘
μ
m
My
„
∑
o
Omega
Römische Ziffern
Römische
Ziffern
Arabische
Ziffern
Römische
Ziffern
Arabische
Ziffern
Römische
Ziffern
Arabische
Ziffern
I
1
XX
20
CC
200
II
2
XXX
30
CCC
300
III
3
XL
40
CD
400
IV
4
L
50
D
500
V
5
LX
60
DC
600
VI
6
LXX
70
DCC
700
VII
7
LXXX
80
DCCC
800
VIII
8
XC
90
CM
900
IX
9
C
100
M
1000
X
10
86 = LXXXIV
99 = XCIX
691 = DCXCI
2016 = MMXVI
Um Verwechslungen zu vermeiden, darf vor einem Zahlzeichen immer nur ein kleineres stehen (z. B. für die
Zahl 48: XLVIII und nicht IIL).
Basisgrößen und Basiseinheiten (SI-Einheiten 1))
Basisgrößen und Basiseinheiten nach DIN 1301-1: 2010-10
Basisgrößen
Basiseinheiten
Name
Häufigste(s)
Zeichen
Länge
§, s, d
Masse
m
Name
Zeichen
Meter
m
Kilogramm
kg
Zeit
t
Sekunde
s
Elektrische Stromstärke
Û
Ampere
A
Thermodynamische Temperatur
T
Kelvin
Stoffmenge
n
Mol
Lichtstärke
Û, Ûv
1)
Candela
SI ist die Abkürzung für Systeme International d’Unitès (Internationales Einheitensystem)
K
mol
cd
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 7
GR
1.1 Allgemeine Grundlagen
Vorsätze vor Einheiten (➞ Potenzrechnung)
Vorsatzzeichen
Y
Vorsatz
Yotta
Z
Bedeutung
24
d
Dezi
10 – 1
21
c
Zenti
10 – 2
18
m
Milli
10 – 3
15
μ
Mikro
10 – 6
12
10
n
Nano
10 – 9
10
Peta
T
Vorsatz
10
Exa
P
Vorsatzzeichen
10
Zetta
E
(nach DIN 1301-1: 2010-10)
Bedeutung
10
Tera
G
Giga
109
p
Pico
10 – 12
M
Mega
106
f
Femto
10 – 15
k
Kilo
103
a
Atto
10 – 18
2
z
Zepto
10 – 21
1
y
Yokto
10 – 24
h
Hekto
da
10
Deca
10
Der Vorsatz gibt den Faktor an, mit dem die Einheit zu multiplizieren ist.
1 kW = 1 · 103 W = 1000 W
1 μm = 1 · 10 – 6 m = 0,000 001 m
Formelzeichen und Einheiten
Name/Bedeutung
(nach DIN 1304-1: 1994-03 und DIN 1301-1: 2010-10)
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Raumgrößen und Zeitgrößen
Abklingkoeffizient
∂
1/s
Ausbreitungsgeschwindigkeit
einer Welle
c
m/s
Beschleunigung
a
m/s2
Breite
b
m
Darüber hinaus gibt es für ganz spezielle
Bereiche der Technik auch Fachnormen.
Dehnung (relative Längenänderung)
™
1
Beispiele:
∂, d
m
f
m
➞
Kältetechnik,
Formelzeichen
Dicke, Schichtdicke
Durchbiegung, Durchhang
Achtung: Formelzeichen und Einheiten
betreffend
DIN 1301-1 (Einheitenzeichen) und DIN 13041 (Formelzeichen) sind Grundformen und die
darin angegebenen Fomelzeichen und Einheitenzeichen sollten möglichst bevorzugt
verwendet werden.
DIN EN 764-1
„Druckgeräte“ für Arbeitstemperatur t0.
DIN 1304-1
für Celsiustemperatur
« oder t.
d, D
m
DIN 1304-1
für Zeit t.
å, ∫, ©
rad
DIN 1304-1
Flächeninhalt, Fläche, Oberfläche
A, S
m2
für (➞) Trockenkugeltemperatur tsic [sic steht
für siccus (trocken)].
Frequenz, Periodenfrequenz
f, ~
Hz
v, u, w, c
m/s
h, H
m
Kreisfrequenz, Pulsatanz
(Winkelfrequenz)
∑
1/s
Länge
§
m
Durchmesser
Ebener Winkel, Drehwinkel
(bei Drehbewegungen)
Geschwindigkeit
Höhe, Tiefe
➞
Formelzeichen,
Regelung
In der Praxis der Klimatechnik steht für
Trockenkugeltemperatur «tr oder qTK. In Analogie: (➞) Feuchtkugeltemperatur qf oder qFK.
Viele weitere Beispiele zeigen, dass es keine
einheitliche Bezeichnungsweise bezüglich
der Formeleichen gibt.
Konsequenz:
In diesem Buch werden die Formelzeichen
entsprechend des gerade anstehenden Technikbereiches gewählt.
7
01 (005 - 039)_ TB San 015-046 GR
8
GR
21.10.13
08:11
Seite 8
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Raumgrößen und Zeitgrößen (Fortsetzung)
Periodendauer,
Schwingungsdauer
Phasenverschiebungswinkel
T
s
ƒ
rad
Radiant
Phasenwinkel
ƒ(t)
rad
Radiant
Querschnittsfläche, Querschnitt
S, q
m2
Radius, Halbmesser, Abstand
r
m
Repetenz (Wellenzahl)
‚
1/m
Ruck
r, h
m/s3
Umdrehungsfrequenz (Drehzahl)
n, fr
1/s
Volumen, Rauminhalt
V, †
m3
V, q v
m3/s
Weglänge, Kurvenlänge
s
m
Wellenlänge
¬
m
Winkelbeschleunigung,
Drehbeschleunigung
å
rad/s2
å = ∑/t bzw. å = ¤∑/¤t
Winkelgeschwindigkeit,
Drehgeschwindigkeit
∑
rad/s
∑=2·π·n
Volumenstrom,
Volumendurchfluss
‚ = 1/¬
Kehrwert der Umdrehungsdauer T: n = 1/T
Q = V/t bzw. Q = A · v
t
s
†, T
s
Absoluter Druck
pabs
Pa
Pascal
1 Pa = 1 N/m2
Arbeit
Joule
W = F · s ; 1 J = 1 Nm
Zeit, Zeitspanne, Dauer
Zeitkonstante
Auch Abklingzeit
Mechanische Größen
W, A
J, Nm
Arbeitsgrad, Nutzungsgrad
Ω
1
Atmosphärische Druckdifferenz,
Überdruck
pe
Pa
Bewegungsgröße, Impuls
p
kg · m/s
Mb
N·m
Dehnung,
relative Längenänderung
™
1
Dichte, Massendichte,
volumenbezogene Masse
®, ®m
kg/m3
Direktionsmoment, winkelbezogenes Rückstellmoment
D
N · m/rad
Drall, Drehimpuls
L
kg · m2/s
H
N·m·s
ı, Δ
rad/m
Biegemoment
Drehstoß
Drillung, Verwindung
Druck
p
Pa
Dynamische Viskosität
ª
Pa · s
Arbeitsverhältnis,
Energieverhältnis
Pascal
pe = pabs – pamb
1 mbar = 1 hPa
™ = ¤§/§
§ = §0 = Ausgangslänge
® = m/V
D = M T /ƒ (ƒ = Torsionswinkel)
Pascal
p = F /A; 1 Pa = 1 N/m2
ª = †/D
† = Schubspannung
D = Schergeschwindigkeit
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 9
1.1 Allgemeine Grundlagen
GR
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Mechanische Größen (Fortsetzung)
Elastizitätsmodul
E
N/m2,
N/mm2
E, W
J
w
J/m3
Flächenbezogene Masse,
Flächenbedeckung
m”
kg/m2
Flächenmoment 1. Grades
H
m3
Flächenmoment 2. Grades
Û
m4
Energie
Energiedichte,
volumenbezogene Energie
Joule
FG, G
N
Gravitationskonstante
G, f
N · m2/kg
Grenzflächenspannung,
Oberflächenspannung
‚, ©
N/m
Isentropische Kompressibilität
çS, Δ
1/Pa
Isothermische Kompressibilität
çT, Δ
1/Pa
~
m2/s
E kin, W kin
J
K
N/m2
Gewichtskraft
Kinematische Viskosität
Kinetische Energie
Kompressionsmodul
E = ‚/™ 1 N/mm2 = 106 N/m2
1 J = 1 Nm = 1 Ws
m” = m/A
Früher: Flächenträgheitsmoment
Newton
F = G · m 1 · m 2 /r 2
G = 6,67259 · 10 – 11 m3/(kg · s2)
~ = ª/®
Joule
Kraft
F
N
Kraftmoment, Drehmoment
M
N·m
E kin = 1/2 · m · v 2
K = – p /«
(« = relative Volumenänderung)
Newton
F=m·a
M=F·r
F = Tangentialkraft
r = senkrechter Abstand zwischen
Drehpunkt und
Wirkungslinie der Kraft
Kraftstoß
Längenbezogene Masse
Û
N·s
m’
kg/m
Leistung
P
W
Leistungsdichte,
volumenbezogene Leistung
ƒ
W/m3
Masse, Gewicht als
Wägeergebnis
m
kg
m, q m
kg/s
Û
kg/(m2 · s)
Massenstrom,
Massendurchsatz
Massenstromdichte
Normalspannung,
Zug- oder Druckspannung
Poisson-Zahl
Potenzielle Energie
Querdehnung
m’ = m/§
Watt
P = W/t
ƒ = w/t
w = Energiedichte
m = m/t
Û = m/S = ® · v
2
‚
N/m ,
N/mm2
μ, ~
1
Epot, Wpot
J
™q
1
μ = ™q /™
Joule
Epot = m · g · h
™q = ¤d/d
(bei kreisförmigem Querschnitt)
9
01 (005 - 039)_ TB San 015-046 GR
10
GR
21.10.13
08:11
Seite 10
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Mechanische Größen (Fortsetzung)
Reibungszahl
Relative Dichte
Relative Volumenänderung,
Volumendilatation
Rohrwiderstandszahl
Rohrreibungszahl
μ, f
1
μ = FR / FN
FR = Reibungskraft
FN = Normalkraft
d
1
«, ª
1
« = ¤V / V bzw.
« (in %) = ¤V · 100 % / V
¬
1
¬ = (p 1 – p 2) · 2 · d / (® · § · v 2)
(bei geradem Rohr mit
kreisförmigem Querschnitt)
Schiebung, Scherung
©
1
Schubmodul
G
N/m2,
N/mm2
Schubspannung
†
N/m2,
N/mm2
Spezifische Arbeit,
massenbezogene Arbeit
Y
J/kg
Y = W/m
Spezifisches Volumen,
massenbezogenes Volumen
v
m3/kg
v = V/m
M t, T
N·m
J
kg · m2
Trägheitsradius
i, r i
m
Umfang
U, §u
m
Umgebender
Atmosphärendruck
pamb
Pa, N/m2
Volumenstrom,
Volumendurchfluss
V, q v
m3/s
Torsionsmoment, Drillmoment
Trägheitsmoment,
Massenmoment 2. Grades
Widerstandskraft
Fw
N
Widerstandsmoment
W
m3, mm3
Wirkungsgrad
ª
1
G=†/©
(© = Schiebung)
Früher: Massenträgheitsmoment
Pascal
Newton
Leistungsverhältnis
Größen der Thermodynamik, Wärmeübertragung und physikalischen Chemie
➞
Anzahl Teilchen, Teilchenzahl
N
1
Affinität einer chemischen
Reaktion
A
J/mol
Avogadro-Konstante
NA, L
1/mol
Boltzmann-Konstante
k
J/K
k = R / NA = 1,380 650 4 · 10 – 23 J / K
(R = universelle Gaskonstante)
t, «, ı
°C
t = T – T0
Chemisches Potenzial
eines Stoffes B
μB
J/mol
Diffusionskoeffizient
D
m2/s
Dissoziationsgrad
å
1
Celsius-Temperatur
➞
Formelzeichen, Regelung
Kältetechnik, Formelzeichen
NA = N / n (n = Stoffmenge)
NA = 6,022 141 79 · 1023 mol – 1
T0 = 273,15 K
å = Ndiss / Nges (Anzahl der
dissoziierten Moleküle zur
Gesamtzahl der Moleküle)
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 11
GR
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Größen der Thermodynamik, Wärmeübertragung und physikalischen Chemie (Fortsetzung)
Enthalpie
H
Entropie
S
J/K
Faraday-Konstante
F
C/mol
Individuelle (spezielle)
Gaskonstante des Stoffes B
RB
J/(kg · K)
Innere Energie
U
J
Isentropenexponent
Δ
1
Ladungszahl eines Ions,
Wertigkeit eines Stoffes B
zB
1
Molalität einer Komponente B
b B, m B
mol/kg
Relative Atommasse eines
Nuklids oder eines Elementes
Ar
1
Zahlenwert gleich dem Zahlenwert für die Atommasse in der
atomaren Masseneinheit u und
gleich dem Zahlenwert der stoffmengenbezogenen Masse M in
g/mol
Relative Molekülmasse
eines Stoffes
Mr
1
Zahlenwert gleich dem Zahlenwert für die Atommasse in der
atomaren Masseneinheit u und
gleich dem Zahlenwert der stoffmengenbezogenen Masse M in
g/mol
Spezifische Enthalpie,
massenbezogene Enthalpie
h
J/kg
Spezifische Entropie,
massenbezogene Entropie
s
J/(kg · K)
Spezifische innere Energie,
massenbezogene innere
Energie
u
J/kg
H o , H o, n
J/kg
Früher: oberer Heizwert
H o, n u. H u, n sind volumenbezogen
J/kg
Früher: unterer Heizwert
Spezifischer Brennwert,
massenbezogener Brennwert
s. Anmerkung
Spezifischer Heizwert,
massenbezogener Heizwert
s. Anmerkung
H u , H u, n
J
F = NA · e (e = Elementarladung)
F = 96 485,3399 C/mol
RB = R / MB
(R = universelle Gaskonstante)
Joule
Für ideale Gase: Δ = c p /c V
➞
Spezifische Wärmekapazität,
massenbezogene Wärmekapazität
c
J/(kg · K)
Spezifische Wärmekapazität
bei konstantem Druck
cp
J/(kg · K)
Spezifische Wärmekapazität
bei konstantem Volumen
cV
J/(kg · K)
Spezifischer Wärmewiderstand
® th
K · m/W
Stöchiometrische Zahl eines
Stoffes B in einer chemischen
Reaktion
~B
1
n, ~
mol
Stoffmenge
Joule
Kältetechnik, Formelzeichen
Anmerkung:
DIN 1304 ist noch gültig, jedoch in
der neuesten Normung wird mit
den Indizes s und i
gearbeitet. Somit:
H o entspricht H s
H u entspricht H i
Die Werte in dieser Tabelle sind in
kJ/kg und in kJ/m3 angegeben. Es
kann eine Umrechnung in die Einheiten
Wh/kg und Wh/m3
erfolgen. Dabei sind die Tabellenwerte lediglich durch 3,6 zu teilen.
n B = m B / M B (m B = Masse des
Stoffes B, MB = stoffmengenbezogene Masse des Stoffes B)
11
01 (005 - 039)_ TB San 015-046 GR
12
GR
21.10.13
08:11
Seite 12
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Größen der Thermodynamik, Wärmeübertragung und physikalischen Chemie (Fortsetzung)
Stoffmengenbezogene (molare)
Masse eines Stoffes B
MB
kg/mol
M B = m B / nB
(m B = Masse des Stoffes B,
n B = Stoffmenge des Stoffes B)
Stoffmengenkonzentration
eines Stoffes B
cB
mol/m3
cB = nB / V
(V = Volumen der Mischphase)
n
mol/s
T, «
K
Kelvin
Kelvin
Stoffmengenstrom
Temperatur,
thermodynamische Temperatur
¤T, ¤t, ¤«
K
Temperaturleitfähigkeit
a
m2/s
(Thermischer) Längenausdehnungskoeffizient
å§ , å
1/K
å§ = ¤§ / (§ · ¤T )
Thermischer Leitwert
G th
W/K
G th = 1/R th
(Thermischer) Spannungskoeffizient
åp
1/K
åp = ¤p / (p · ¤T )
(Thermischer) Volumenausdehnungskoeffizient
åV, ©
1/K
åV = ¤V / (V · ¤T )
Thermischer Widerstand,
Wärmewiderstand
R th
K /W
R th = ¤T / Q
(Q = Wärmestrom)
(Universelle) Gaskonstante
R
J/(mol · K)
Verhältnis der spezifischen
Wärmekapazitäten
©, Δ
1
Q
J
Temperaturdifferenz
Wärme, Wärmemenge
Joule
3
J/m
k
W/(m2 · K)
Q, Ïth , Ï
W
Watt
Ampere
Wärmedurchgangskoeffizient
Wärmestrom
R = 8,314 472 J/(mol · K)
© = cp / cV
in der Praxis meist Δ
w th
Wärmedichte, volumenbezogene Wärme
in der Praxis auch °C
k-Wert, nach DIN EN
ISO 6946 auch U-Wert
U=k
Elektrische und magnetische Größen
Elektrische Durchflutung
ı
A
Elektrische Feldkonstante
™0
F/m
Elektrische Feldstärke
E
V/m
Elektrische Flussdichte
D
C/m2
™0 = 8,854 187 817 pF/m
Elektrische Kapazität
C
F
Faraday
Elektrische Ladung
Q
C
Coulomb
©, ‚, Δ
S/m
Elektrische Spannung,
elektrische Potenzialdifferenz
U
V
Elektrische Stromdichte
J
A/m2
Elektrische Leitfähigkeit,
Konduktivität
Elektrische Stromstärke
Elektrischer Fluss
Elektrischer Leitwert
C = Q /U
© = 1/® (® = spezifischer
elektrischer Widerstand)
Volt
J = Û/ S (S = Leiterquerschnitt)
Û
A
Ampere
‡, ‡e
C
Coulomb
G
S
Siemens
heute meist
A für Oberflächen
S für Querschnittsflächen
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 13
GR
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Elektrische und magnetische Größen (Fortsetzung)
R
„
Elektrisches Dipolmoment
p, pe
C·m
Elektrisches Potenzial
ƒ, ƒe
V
Volt
Elementarladung
e
C
Coulomb
Ladung eines Protons,
e = 1,602 176 487 · 10 – 19 C
Energie, Arbeit
W
J
Joule
1 J = 1 Nm = 1 Ws
Flächenladungsdichte,
Ladungsbedeckung
‚
C/m2
Induktivität, Selbstinduktivität
L
H
Elektrischer Widerstand,
Wirkwiderstand, Resistanz
Magnetische Feldkonstante
μ0
H/m
Magnetische Feldstärke
H
A/m
Magnetische Flussdichte
B
T
Magnetische Spannung
Ohm
Henry
μ0 = 1,256 637 061 4… μH/m
Tesla
B=ƒ/S
V, Vm
A
Magnetischer Fluss
Ï
Wb
Permeabilität
μ
H/m
Permeabilitätszahl,
relative Permeabilität
μr
1
Permittivität
™
F/m
™=D/E
Permittivitätszahl,
relative Permittivität
™r
1
™r = ™ / ™0
®, ®e, ª
C/m3
®
„·m
Raumladungsdichte,
Ladungsdichte,
volumenbezogene Ladung
Spezifischer elektrischer
Widerstand, Resistivität
Windungszahl
Wirkleistung
N
1
P, Pp
W
Weber
μr = μ / μ0
1 „ · m = 100 „ · cm
1 „ · m = 10 6 „ · mm2 / m
Watt
Größen elektromagnetischer Strahlungen
Absorptionsgrad
å, a
1
Beleuchtungsstärke
Ev
lx
Brechwert von Linsen
D
1/m
D=n/f
n = c0 / c
Brechzahl
n
1
Brennweite
f
m
Emissionsgrad
™
1
Leuchtdichte
Lv
cd/m2
Lichtgeschwindigkeit
im leeren Raum
c0
m/s
Lichtmenge
Qv
lm · s
Lichtstärke
Ûv
cd
Lux
c 0 = 2,997 924 58 · 10 8 m/s
Candela
13
01 (005 - 039)_ TB San 015-046 GR
14
GR
21.10.13
08:11
Seite 14
1.1 Allgemeine Grundlagen
Formelzeichen und Einheiten (Fortsetzung)
Name/Bedeutung
Formelzeichen
SI-Einheit
Zeichen
Name
Bemerkung/wichtige Beziehungen
Größen elektromagnetischer Strahlungen (Fortsetzung)
Lichtstrom
Ïv
Im
Reflexionsgrad
®
1
Stefan-Boltzmann-Konstante
‚
W/(m2 · K4)
Q e, W
J
Strahlungsenergiedichte,
volumenbezogene Strahlungsenergie
w, u
J/m3
Strahlungsleistung,
Strahlungsfluss
Ïe, P
W
Transmissionsgrad
†
1
Strahlungsenergie,
Strahlungsmenge
Lumen
‚ = 5,670 400 · 10 – 8 W/(m2 · K 4)
Joule
Watt
Größen der Atom- und Kernphysik
Äquivalentdosis
H
Sv
Sievert
Aktivität einer radioaktiven
Substanz
A
Bq
Bequerel
Atommasse
ma
kg
Bohr-Radius
a0
m
Energiedosis
D
Gy
Gyromagnetischer Koeffizient
©
A · m2/(J · s)
T1/2
s
Ionendosis
J
C/kg
Kerma
K
Gy
Magnetisches (Flächen-)
Moment eines Teilchens
μ
A · m2
Halbwertszeit
Mittlere Lebensdauer
†
s
Neutronenzahl
N
1
Nukleonenzahl, Massenzahl
A
1
Planck-Konstante, Planck’sches
Wirkungsquantum
h
J·s
Protonenzahl
Z
1
Reaktionsenergie
Q
J
Ruhemasse des Elektrons
me
kg
Rydberg-Konstante
R∞
1/m
å
1
Teilchenstrom
Û
1/s
Zerfallskonstante
¬
1/s
p
Pa, N/m2
Schallgeschwindigkeit
c, c 0
m/s
Schallintensität
Û, J
W/m2
Schallleistung
P, Pa
W
Sommerfeld-FeinstrukturKonstante
a0 = 0,529 177 208 59 · 10 – 10 m
Gray
T1/ 2 = † · ln 2
Gray
A=Z+N
h = 6,626 068 96 · 10 – 34 J · s
Joule
me = 9,109 382 15 · 10 – 31 kg
R = 10 973 731,568 527 m – 1
å = 7,297 352 5376 · 10 – 3
¬=1/†
Größen der Akustik
Schalldruck
Pascal
Watt
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 15
1.2 Allgemeine Mathematik
GR
Grundrechenarten
Addition (Zusammenzählen)
Gemeine Brüche
Natürliche Zahlen
15
+
26
41
=
Summand plus Summand gleich Summe
2 6 2+6 8
+ = = = 2
4 4
4
4
Mögliche Rechenschritte:
15 + 26 = 15 + (5 + 21) = (15 + 5) + 21 = 20 + 21
= 20 + (20 + 1) = (20 + 20) + 1 = 40 + 1 = 41
Beachte:
8 + (–6) = 8 – 6 = 2
Bei gleichnamigen Brüchen die Zähler unter Beibehaltung des Nenners addieren und dann, wenn
möglich, kürzen:
(vgl. Klammerregeln)
Ungleichnamige Brüche zunächst durch Hauptnennerbildung (vgl. Bruchrechnen) und Zählererweiterung gleichnamig machen:
1 2 1·3 2·2 3 4 7
1
+ = + = + = = 1 2 3 2·3 3·2 6 6 6
6
Gemischte Zahlen zunächst in unechte Brüche verwandeln (vgl. Bruchrechnen)
Allgemeine Zahlen
Größen
a + a = 2a
Nur gleichartige Größen lassen sich addieren.
Eventuell müssen Einheiten umgerechnet werden!
a+b=c
5 kg + 7 kg = 12 kg
a + b = b + a (Kommutativgesetz)
8,0 kg + 500 g = 8,0 kg + 0,5 kg = 8,5 kg
a + (b + c) = (a + b) + c = a + b + c
(Assoziativgesetz)
6,00 m + 40 cm = 600 cm + 40 cm = 640 cm
Subtraktion (Abziehen)
Natürliche Zahlen
14
–
Gemeine Brüche
8
=
6
Minuend minus Subtrahend gleich Differenz
16 – (8 – 3) = 16 – 8 + 3 = 11
Bei gleichnamigen Brüchen die Zähler unter Beibehaltung des Nenners voneinander subtrahieren
und dann, wenn möglich, kürzen:
3 1 3–1 2
– = = = 1
2 2
2
2
16 – (8 + 3) = 16 – 8 – 3 = 5
Klammerregeln beachten (vgl. Klammerrechnung)
Ungleichnamige Brüche zunächst durch Hauptnennerbildung (vgl. Bruchrechnen) und Zählererweiterung gleichnamig machen:
7 2 7 · 3 2 · 8 21 16 21 – 16 5
– = – = – = = 8 3 3 · 8 3 · 8 24 24
24
24
Gemischte Zahlen zunächst in unechte Brüche verwandeln (vgl. Bruchrechnen)
Allgemeine Zahlen
Größen
3a – 2a = 1a = a
Nur gleichartige Größen lassen sich voneinander
subtrahieren. Eventuell müssen Einheiten umgerechnet werden.
a – b = c (c = Differenz aus a und b)
ab – (c – d) = ab – c + d
16 m3 – 4 m3 = 12 m3
ab – (c + d) = ab – c – d
5,0 m3 – 100 dm3 = 5,0 m3 – 0,1 m3 = 4,9 m3
Klammerregeln beachten (vgl. Klammerrechnung)
2,000 L – 58 mL = 2000 mL – 58 mL = 1942 mL
15
01 (005 - 039)_ TB San 015-046 GR
16
GR
21.10.13
08:11
Seite 16
1.2 Allgemeine Mathematik
Grundrechenarten (Fortsetzung)
Multiplikation (Vervielfachen)
Gemeine Brüche
Natürliche Zahlen
6
·
4
24
=
Faktor mal Faktor gleich Produkt oder
Multiplikand mal Multiplikator gleich Produkt
Das Produkt 6 · 4 ist die Kurzschreibweise für die
Summe 6 + 6 + 6 + 6 bzw. 4 + 4 + 4 + 4 + 4 + 4.
Zwei Brüche werden miteinander multipliziert,
indem man Zähler mit Zähler und Nenner mit Nenner multipliziert. Dabei kann vor dem Multiplizieren
gekürzt werden.
5 ·
3=
5 ·
1 = 5
5 · 3 = 6 4 6 ·4 2 ·4 8
Beachte: Jede Zahl mit 0 multipliziert ergibt 0, z. B.
3 ·
5=
3 ·
1 = 3 = 1 1
3 · 5 = 10
2
2
2
10
5·0=0
Gemischte Zahlen werden zunächst in unechte
Brüche verwandelt (vgl. Bruchrechnen)
Allgemeine Zahlen
Größen
a · b = ab bzw. a · b = c (c = Produkt aus a und b)
a·0=0
Zwei Größen werden miteinander multipliziert,
indem man Zahlenwerte (Maßzahlen) und Einheiten miteinander multipliziert:
a · b = b · a (Assoziativgesetz)
4 m · 6 m = 4 · 6 · m · m = 24 m2
a · (b + c) = ab + ac (Distributivgesetz)
10 N · 2 m = 20 Nm
Vorzeichenregeln:
(+a) · (+b) = ab
(+a) · (–b) = –ab
(–a) · (–b) = ab
(–a) · (+b) = –ab
Klammerregeln beachten (vgl. Klammerrechnung)
Division (Teilen)
Natürliche Zahlen
Gemeine Brüche
10
:
5
=
2
10
/
5
=
2
oder
Dividend durch Divisor gleich Quotient
Man dividiert durch einen Bruch, indem man mit
dem Kehrbruch (Kehrwert) multipliziert:
oder
3 ·
5=
1
5 bzw.
3 : 4 = 3 · 5 = 8 5 8 4 8 · 4 32
1
0 = 5 (10 = Zähler, 2 = Nenner, 5 = Quotient)
2
Beachte: Eine Division durch 0 gibt es nicht!
3 ·
5=
1
5 = 7 1
3 : 2 = 3 · 5 = 5
2
2
2
2
3
8
3 ·
5=
1
5
=
4 8 · 4 32
5
Bei der Division durch eine gemischte Zahl wird diese zunächst in einen unechten Bruch verwandelt.
Allgemeine Zahlen
Größen
a = a : b = c (c = Quotient aus a und b, b 0)
b
Zwei Größen werden durcheinander dividiert,
indem man Zahlenwerte (Maßzahlen) und Einheiten durcheinander dividiert:
ad
a : c = a · d = b d b c bc
a : (b : c) = a : b =
c
c ac
a
= a · = b b
b
c
3
6m
m3 = 3 m · m
·m=3m
= 6 · 2 m2 2 m2
m·m
2
0 · N = 5 N
20
N=
4 m2 4 m2
m2
Vorzeichenregeln:
(+ a) = a
(+ b) b
(– a) = – a
(+ b)
b
(– a) = a
(– b) b
(+ a) = – a
(– b)
b
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 17
GR
1.2 Allgemeine Mathematik
Klammerrechnung (Rechnen mit Summen)
Steht ein „+“-Zeichen vor der Klammer, so kann diese entfallen, ohne dass sich der Wert der Summe ändert:
a + (2b – 3c) = a + 2b – 3c
5 + (6 – 3) = 5 + 6 – 3 = 8
Steht ein „–“-Zeichen vor der Klammer, so müssen bei deren Weglassen alle innerhalb der Klammer vorhandenen Vorzeichen umgekehrt werden:
– (3a + 2b – c) = –3a – 2b + c
12 – (2 + 8 – 6) = 12 – 2 – 8 + 6 = 8
Klammerausdrücke (bzw. Summen) werden miteinander multipliziert, indem jedes Glied der einen Klammer
mit jedem Glied der anderen Klammer multipliziert wird:
(a + b)2 = (a + b) (a + b) = a 2 + 2ab + b 2 ⎫
⎪
(a – b)2 = (a – b) (a – b) = a 2 – 2ab + b 2 ⎪ Binomische
⎬
⎪ Formeln
(a + b) (a – b) = a 2 – b 2
⎪
⎭
(a + b)c = ac + bc
d (ab – c) = abd – cd
(a + b) (c + d) = ac + ad + bc + bd
(a + b) (c – d) = ac – ad + bc – bd
eispiele praktischer Formeln:
L = L0 (1 + å ¤T ) = L0 + L0 å ¤T
p = x1p1 + (1 – x1)p2 = x1p1 + p2 – x1p2
Q = kA (T1 – T2) = kAT1 – kAT2
n2 + n + n + 1 = n2 + 3 n + 1
L = 1 (n + 2) (n + 1) = (n + 1) (n + 1) = 2
2
2 2
2
2
Klammerausdrücke (bzw. Summen) werden durch einen Divisor (Nenner) dividiert, indem jedes Glied der
Klammer (bzw. jeder Summand des Zählers) durch den Divisor (Nenner) dividiert wird:
a+b
a
b
1 1
a) Division durch ein Produkt: = + = + ab
ab ab b a
a+b–c
a
b
c
b) Division durch eine Summe: (a + b – c) : (a – d) = = + – a–d
a–d a–d a–d
eispiele praktischer Formeln:
Vth – Vv
Vv
ªv = = 1 – Vth
Vth
h2 – h0 m0 (h2 – h0) m0 h2 – m0 h0
m h2
m h0
m1 = m0 – 0
= = = 0
h2 – h1
h2 – h1
h2 – h1
h2 – h1 h2 – h1
Gemeinsame oder beliebige Faktoren, die in jedem Summanden (bzw. Glied) der Klammer vorkommen, können vor die Klammer gezogen (ausgeklammert) werden:
(ab + ac) = a (b + c)
(– 25 – 5p) = – 5 (5 + p)
$
%
2x + y
(2x + y) – 10b = 10b – 1
10b
Ausdrücke (Summen) mit mehreren Klammern werden umgewandelt, indem man die Klammern von innen
her auflöst:
a – {b + [3c – (2d + b)]} = a – {b + [3c – 2d – b]} = a – {b + 3c – 2d – b} = a – b – 3c + 2d + b = a – 3c + 2d
eispiel einer praktischen Formel:
h = c L (T – T0) + Y [h V + c D (T – T0)] = c LT – c LT0 + Y [h V + c DT – c DT0] = c LT – c LT0 + Yh V + Yc DT – Yc DT0
17
01 (005 - 039)_ TB San 015-046 GR
18
GR
21.10.13
08:11
Seite 18
1.2 Allgemeine Mathematik
Bruchrechnung
Erweitern und Kürzen
Hauptnennerbildung
Zähler und Nenner des Bruches werden mit der gleichen Zahl multipliziert oder durch die gleiche Zahl
dividiert:
1. Produktbildung aus den beteiligten Nennern:
3 2 3·3 2·8
9
16
9 + 16 25
+=+=+==
8 3 8 · 3 3 · 8 24 24
24
24
3
3·5
15
= =
4
4·5
20
(Erweitert mit der Zahl 5)
16 16 : 4 4
= =
12 12 : 4 3
Der Zähler wird mit dem gleichen Faktor erweitert, der beim Nenner erforderlich ist, um den
Hauptnenner zu erhalten.
(Gekürzt mit der Zahl 4)
a
c
a·d
c · (a + b)
+ = + a + b d (a + b) · d d · (a + b)
ad + c (a + b)
= d (a + b)
Gekürzt werden darf nur aus Produkten, nie aus
Summen:
a (b – 1)
b–1
ab – a
= =
2ab
2ab
2b
(Gekürzt mit a. Aus der
Summe kann b nicht
gekürzt werden.)
2. Suche nach dem kleinsten gemeinsamen Vielfachen (kgV) der beteiligten Nenner:
a) Zerlegung aller Nenner in ihre kleinsten Faktoren,
b) Anordnung der Faktoren entsprechend dem
unten gezeigten Schema,
c) Produktbildung aus allen vorkommenden
Faktoren (diese jeweils in der Anzahl ihrer
größten Häufigkeit in einer Zeile).
Umwandeln gemischter Zahlen in unechte
Brüche
Zum Produkt aus Nenner und ganzer Zahl wird der
Zähler addiert. Dies ergibt den Zähler des unechten
Bruches:
Beispiel:
6 · 3 + 2 20
2
6 ==
3
3
3
1
1
2
8
5
++++
14
3
10
60
72
Umwandeln unechter Brüche in gemischte
Zahlen
Der Zähler des unechten Bruches wird in eine Summe zerlegt, die den größten Summanden enthält,
der noch ohne Rest durch den Nenner teilbar ist.
Dann – nach dem Auftrennen in zweiTeilbrüche – kürzen:
3
3
18 15 + 3 15 3
==+=3+=3 5
5
5
5
5
5
1 · 180 + 1 · 840 + 2 · 252 + 8 · 42 + 5 · 35
= = 0,808
2520
Nenner kleinste Faktoren
Erweiterungsfaktor
für den Zähler
14
3
10
60
72
2
2 · 2 · 3 · 3 · 5 = 180
2 · 2 · 2 · 3 · 5 · 7 = 840
2 · 2 · 3 · 3 · 7 = 252
2 · 3 · 7 = 42
5 · 7 = 35
k. g. V.
2 · 2 · 2 · 3 · 3 · 5 · 7 = 2520 = Hauptnenner
·7
3
2
·5
2·2 ·3 ·5
2 · 2· 2· 3· 3
Prozentrechnung
Formeln
Beispiele
p
p % von G = · G = P
100
20 % von
p Prozentsatz
G Grundwert
P Prozentwert
20
1200 kg = · 1200 kg = 240 kg
100
Prozentsatz Grundwert
Prozentwert
p·G
P=
100 %
20 % von 1200 kg
sind 240 kg
20 % · 1200 kg
= 240 kg
100 %
100 % · P
p = G
240 kg von 1200 kg
entsprechen einem
Anteil von 20 %
100 % · 240 kg
= 20 %
1200 kg
100% · P
G = p
Wenn 240 kg einem
Anteil von 20 % ent- 100 % · 240 kg
= 1200 kg
sprechen, beträgt der 20 %
Grundwert 1200 kg
01 (005 - 039)_ TB San 015-046 GR
21.10.13
08:11
Seite 19
GR
1.2 Allgemeine Mathematik
Potenzrechnung
Zehnerpotenzen
Zahlen über 1
Zahlen unter 1
Zahlen über 1 können als Vielfache von Zehnerpotenzen dargestellt werden, mit einem positiven
Exponenten, dessen Wert um 1 niedriger liegt, als
die Zahl Stellen vor dem Komma besitzt:
Zahlen unter 1 können als Vielfache von Zehnerpotenzen dargestellt werden, mit einem negativen
Exponenten, dessen Wert der Anzahl der Stellen entspricht, um die das Komma der Ausgangszahl nach
rechts gerückt wurde:
1253,65 = 1,25365 · 1000 = 1,25365 · 103
25
2,5
2,5
0,0025 = = = = 2,5 · 10–3
10 000 1000 103
101 = 10
104 = 10 000
2
100 = 1
1
10–3 = = 0,001
1000
1
10–1 = = 0,1
10
1
10–4 = = 0,000 1
10 000
1
10–2 = = 0,01
100
1
10–5 = = 0,000 01
100 000
5
10 = 100
10 = 100 000
103 = 1 000
106 = 1000 000
1
10–6 = = 0,000 001
1000 000
eispiele aus der Praxis:
1
Längenausdehnungszahl von Stahl: å = 1,2 · 10–5 K–1 = 0,000 012 K
Avogadro-Konstante: NA = 602 213 670 000 000 000 000 000 ≈ 6,022 · 1023
Potenzrechnung allgemein
Regeln
Beispiele
m
a = a · a · a · . . . (m Faktoren)
a = Basis (Grundzahl); m = Exponent (Hochzahl);
am = Potenz
54 = 5 · 5 · 5 · 5 = 625
5 = Basis; 4 = Exponent;
54 = Potenz (vierte Potenz von 5)
a1 = a; a0 = 1 (für a 0)
121 = 12; 120 = 1
–m
a
1
1
=
; = am (für a 0)
am a–m
1
1
1
10–3 = = = 0,001; = 102 = 100
10 3 1000
10–2
W
5 Wm–2 K–1 = 5 m2K
am · an = am+n
32 · 33 = 32+3 = 35 = 243
am
am : an = = am–n
an
43
= 43–2 = 41 = 4
43 : 42 = 42
T1 4
T14
42
4 2
= = 22 = 4; E = ™ · C · = ™ · C · 22
2
100
100 4
@ #
am
a
= bm
b
m n
m·n
(a ) = a
@#
m
n m
= (a )
2 3
2·3
(6 ) = 6
2
@ #
6
= 6 = 46 656
2
(ab)m = ambm
(3 · 5) = 3 · 52 = 9 · 25 = 225
(5 m)2 = 52 m2 = 25 m2
(–a)m = positiv für gerade m,
negativ für ungerade m
(–2)4 = (–2) · (–2) · (–2) · (–2) = 16
(–3)3 = (–3) · (–3) · (–3) = –27
19