TechMech Zusammenfassung 1. Grundlagen 2. Statik

TechMech Zusammenfassung
Andreas Biri, D-ITET
31.07.13
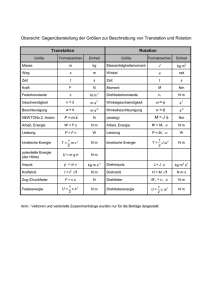
Ebene & räumliche Bewegungen
Drehmoment M
Eine starre ebene Bewegung ist entweder eine
Das Drehmoment ist vom Bezugspunkt abhängig:
⃗⃗⃗⃗⃗
Translation: alle Punkte haben parallele Geschwindigk.
1. Grundlagen
Rotation: min. zwei Punkte haben nichtparallele Geschw.
Zylinderkoordinaten
Bei räumlichen Bewegungen unterscheidet man:
⃗
⃗⃗⃗⃗
⃗⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗
̇ ⃗⃗⃗⃗
⃗⃗⃗
̇ ⃗⃗⃗⃗
⃗⃗⃗⃗
Kann Kraft entlang Wirkungslinie verschieben!
|⃗⃗⃗⃗⃗ |
Moment bezüglich Achse
Schraubung: Rotation um Achse sowie Translation entlang
1. Projiziere Kraft auf Ebene senkrecht zu Achse
2. Multipliziere Betrag mit Abstand zur Achse d
3. Vorzeichen aus Korkenzieherregel
der Rotationsachse
minimale Anzahl benötigter Lagekoordinaten
Zahl d. freien Geschwindig. – und Rotationskomponenten
⃗⃗⃗⃗⃗⃗
Kreiselung: ein Punkt des Körpers bleibt fixiert (mom. Rotation)
⃗⃗⃗⃗
Freiheitsgrade
[Nm]
Satz vom Momentanzentrum
Lote auf Geschwindigkeiten geben Momentanzentrum
Auflager sind stets Momentanzentren
Bei einer Rotation um das Momentanzentrum M gilt:
Leistung P
|⃗⃗⃗⃗ |
⃗⃗⃗⃗⃗
|⃗⃗⃗ |
⃗⃗⃗⃗
[ 1 W = 1 J/s]
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
⃗
Polbahn: Kurve des Mom.zentrum im Verlauf der Bewegung
leistungslos :
n : Freiheitsgrade d. einzelnen Körper
b : lin. unabhängige Bindungsgleichungen
Kinemate
Starrer Körper: FG 6 im Raum, FG 3 in der Ebene
Die Geschwindigkeit eines Punktes setzt sich zusammen
Bei reiner Rotation gilt:
aus dessen Translationsgeschwindigkeit ⃗⃗⃗⃗ und der
Geschwindigkeit & Schnelligkeit
Rotationsgeschwindigkeit ⃗⃗⃗
⃗⃗⃗⃗
Geschwindigkeit:
( )
̇ ⃗⃗⃗
̇ ⃗⃗⃗⃗
̇ ⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗
̇
2. Statik
⃗⃗⃗⃗⃗
⃗⃗⃗
Reduktion von Kräftegruppen
⃗⃗⃗⃗⃗⃗⃗
Die Invarianten der Kinematen sind unabhängig vom
Schnelligkeit:
Bezugssystem:
| |
√ ̇
̇
̇
⃗⃗
⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗⃗⃗
Bei einem starren Körper verschieben sich die Punkte in d. gleiche Richtung
⃗⃗⃗⃗⃗
⃗⃗⃗⃗
|⃗⃗⃗⃗ |
⃗⃗⃗⃗⃗⃗
|⃗⃗⃗⃗ |
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗
Translation:
Rotation:
Schraubung:
⃗⃗⃗
∑ ⃗⃗⃗
Resultierendes Moment ⃗⃗⃗⃗⃗⃗ zum Bezugspunkt O:
Satz der projizierten Geschwindigkeiten (SdpG)
⃗⃗⃗⃗⃗
Resultierende ⃗⃗ : Summe der Kräfte der Kräftegruppe
( ⃗⃗⃗⃗⃗
⃗⃗⃗⃗ )
⃗⃗⃗⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗
Gesamtleistung P bei einer Starrkörperbewegung
⃗⃗
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗
⃗⃗⃗
1
1.
( { ⃗⃗⃗ } )
( { ⃗⃗ } )
Statisch unbestimmt: „klemmt“
Schwerpunkt / Kräftemittelpunkt
Statische Äquivalenz
⃗⃗⃗⃗
⃗⃗⃗
⃗⃗⃗
∫⃗
⃗⃗⃗
∑
2. Dynamen (Resultierende u. resultierendes Moment) gleich
Für zwei Kräfte : vektoriell gleich und selbe Wirkungslinie
Für homogene Verteilung:
⃗⃗⃗
Kinematisch bestimmt: falls aufgrund der Lagerung keine
∫⃗
zulässigen (Starrkörper-) Bewegungen mehr möglich sind
⃗⃗⃗⃗⃗
∑
Kinematisch unbestimmt : System ist beweglich ; kann
Kräftepaar: „ freies Moment“
⃗⃗⃗
Besteht aus zwei Kräften gleichen Betrags in
entgegengesetzte Richtung:
⃗
∫⃗
∑
nicht statisch bestimmt sein
⃗⃗⃗⃗⃗
∑
⃗⃗⃗
Kräftemittelpunkt:
⃗⃗⃗
⃗⃗
Reibung
⃗⃗⃗
Moment ist unabhängig von Bezugspunkt!
⃗⃗⃗⃗⃗
∑
Haftreibungskraft
| |
Dyname
| |
Prinzip der virtuellen Leistungen (PdvL)
Eine Kräftegruppe wird durch ihre Dyname bestimmt:
⃗
Ein System ist genau dann in Ruhelage, wenn virtuelle
Gesamtleistung für alle Bewegungszustände verschwindet:
⃗⃗⃗⃗⃗
̃
̃(
)
̃(
)
̃
⃗ : Resultierende
⃗⃗⃗⃗⃗ : Resultierendes Moment
Gilt auch für konstante (Rotations-) Geschwindigkeiten
Transformationsregel
Zulässiger virtueller Bewegungszustand: verletzt keine Bindungen
⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗
⃗⃗
Die Invarianten der Dynamen sind unabhängig vom
Bezugssystem:
⃗
⃗
Nullsystem:
⃗
⃗⃗⃗⃗⃗
Kräftepaar:
⃗
⃗⃗⃗⃗⃗
Einzelkraft:
⃗
Schraube:
Grad der Unbestimmtheit:
Hauptsatz der Statik
Stellt zusätzliche Unbekannte dar und dient lediglich
nachträglich zur Überprüfung, ob Ruhe wirklich möglich ist.
Gleitreibungskraft
| |
| |
| |
Entgegen d. Bewegungsrichtung:
⃗⃗⃗⃗⃗
|
|
Liefert stets eine zusätzliche Gleichung zum Lösen des GS
Ein starrer Körper befindet sich genau dann in einer
Ruhelage, wenn die äusseren Kräfte im Gleichgewicht sind:
⃗⃗
⃗⃗⃗⃗⃗
Rollwiederstand (Deformation)
⃗⃗⃗⃗⃗⃗
|
| |
|
In Bewegung (entgegengesetzt zu Rotationsrichtung):
Statische Bestimmtheit
|
|
| |
⃗⃗⃗⃗⃗
| |
⃗⃗⃗⃗⃗⃗
| |
Bindung: Einschränkung der Bewegungsfreiheit
Statisch bestimmt:
ideal rau:
2
̈
̇
Beschleunigung:
Trägheitskraft:
Trägheitsmomente einfacher Körper
Drallsatz
3. Dynamik
̈
̈
̈
Drallsatz bezüglich inertialen (in Ruhe) Punkts O
∭
Trägheitskraftdichte
( )
( )
̃(
)
̃(
)
∭
̃(
)
̃
Newton’sches Bewegungsgesetz
̇
4. Problemlösungsverfahren
Drallsatz bezüglich dem Massenmittelpunkt C
⃗
∭
Massenmittelpunktsatz: kann ausgedehnter Körper wie
̇
Massenpunkt im Schwerpunkt betrachten
Kinetische Energie
PdvL : für einzelne Kräfte
1. Stab ausschneiden , Zugkräfte einführen
Umrechnungsformel
2. Bewegungszustand wählen: zB. führe Rotation
ein,
s.d. immer noch wirkliche Bewegung und Lagerungskräfte
sollen nicht bei Leistungsberechnung vorkommen
DS bezüglich 0: praktisch für Kreiselung um O
Impuls
DS für relativen Drall: gut für beschleunigt bewegtes C
∭
Drallsatz für ebene Bewegungen
̇
⃗⃗
(
⃗⃗⃗⃗ )
⃗⃗⃗⃗
Impulserhaltung
HS : für alle Lager- und Bindungskräfte
Komponentenbedingungen (KB) :
̇
Impulssatz / Massenmittelpunktsatz
̇
Momentenbedingungen (MB) :
̇
1. Wenn möglich bei Schnittpunkten; will diese ja meistens
Drallrichtung und Moment besitzen selben Richtungssinn !
nicht berechnen, sollen nicht vorkommen in Gleichung
Massenträgheitsmoment
2. freies Moment darf überall angesetzt werden!
+ Zusatzbedingungen:
∬
Inelastischer Stoss:
1.
Elastischer Stoss (Energieerhaltung) :
Drallsatz bezüglich des Massenmittelpunktes C
̇
Stosszahl k : (
3. -> P = 0 , auflösen auf gesuchte Variabel
)
(
)
k = 0 : vollkommen inelastisch ; k = 1 : vollkommen elastisch
2. falls
: Seilkraft immer positiv, da nur Zugkraft möglich
: Knickgefahr bei Pendelstütze
̇
Kinematische Relation: Sind Koordinaten miteinander
Kinematische Relation ̇
̇ ?
verbunden? (zB. Rolle ̇
̇)
3
Anwendung des Hauptsatzes der Statik
1. System freischneiden und angreifende Kräfte einführen:

Gewichtskräfte greifen im Schwerpunkt an

Seil- und Stabkräfte als Zugkräfte

Normalkräfte senkrecht zu r Bewegungsebene
Winkel & Approximationen
5. Verschiedenes
DGL-Lösungen
( )
̈
( )
̈
( )
(eventuell weitere Unbekannte für Angriffspunkt)
̈
(
)
(
)
3. Zweckmässiges Koordinatensystem finden
3. Gleichgewichtsbedingungen formulieren (KB, MB)
4. Gleichungen und Unbekannte abzählen; bei zu vielen
Rollendes Rad
Unbekannten aufschneiden
(
5. Lösen und Resultate diskutieren

Ist Seil gespannt:

Körper kippt nicht:

Körper bleibt in Ruhe: | |
)
̇(
(
)
?
)
̈(
̇
)
̇
̈
| |
̇
̇
̇
Lösung von Dynamikproblemen
1. System freischneiden und in allgemeiner Lage
̇
Zylinderkoordinaten
̇ ⃗⃗⃗⃗
angreifende Kräfte einführen
2. Zweckmässiges Koordinatensystem aufstellen und
( ̈
̇ )
kinematische Relationen aufstellen.
Polarkoordinaten: ̈
3. Differentialgleichungen mittels Massenmittelpunktsatz
Kreiskoordinaten: ̈
und Drallsatz aufstellen
Energieerhaltung
4. Bindungskräfte bestimmen und aus den
̇ ⃗⃗⃗⃗
(
̈
⃗⃗⃗⃗
̇ ̇)
̈
Schwerpunkte ebener Flächen
̇
In einem geschlossenen System ist die Summe der
Bewegungsgleichungen eliminieren
potentiellen und kinetischen Energie konstant:
5. Anfangsbedingungen formulieren und gesuchte Grössen
berechnen
6. Resultat diskutieren: zB.
̈
4
5