Versuch 17: Geometrische Optik/ Mikroskop

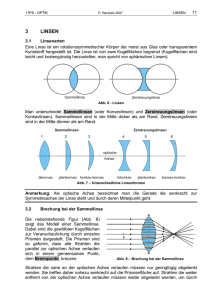
Versuch 17: Geometrische Optik/
Mikroskop
Mit diesem Versuch soll die Funktionsweise von Linsen und Linsensystemen und deren Eigenschaften untersucht werden. Dabei werden das Mikroskop und Abbildungsfehler bei Linsen genauer behandelt.
Vorkenntnisse
Funktionsweise von Sammel- und Zerstreuungslinsen – virtuelle und reelle Abbildung – Funktion von Blenden – Apertur – Dünne Linsen – Dicke Linsen – Linsensysteme – Brennweite –
Schärfentiefe – Auflösungsvermögen – Tubuslänge
Linsenfehler: Sphärische und chromatische Aberration – Astigmatismus – Koma
Optische Geräte: Lupe – Mikroskop – Kondensorlinse – Achromat
Physikalische Grundlagen
Strahlengang
Zur Erklärung des physikalischen Lichtverhaltens wird das Licht als Lichtstrahl betrachtet. Als
Näherung wird angenommen, dass Lichtstrahlen sich immer geradlinig ausbreiten und ihre Richtung nur dann ändern, wenn sie auf eine Grenzfläche treffen. Der Wellencharakter des Lichts
wird vernachlässigt. Mehrere Lichtstrahlen werden als Lichtbündel behandelt. Wichtig bei diesem Modell ist das Prinzip der Umkehrbarkeit, das heißt, dass jeder Strahlengang auch dann
allen optischen Gesetzen genügt, wenn die Ausbreitungsrichtung des Lichts umgekehrt wird. Zudem beeinflussen sich Lichtstrahlen nicht gegenseitig. Die charakterisierenden Eigenschaften des
Lichts im Rahmen der geometrischen Optik können innerhalb dieses Modells gut erfasst wer~ beschrieben. Im Zusammenhang
den. Der Energietransport wird durch den Poynting-Vektor S
~
damit steht die Intensität, welche dem Betrag des über einige Perioden gemittelten Vektors S
entspricht. Es gilt:
I = 0 c n E
2
(1)
Zudem können einem Lichtstrahl eine Polarisation und eine Fortpflanzungsgeschwindigkeit zugeordnet werden. Welleneigenschaften wie die Wellenlänge charakterisiert anschaulich die Farbe
des Lichtstrahls. Das Farbspektrum in dem sichtbaren Bereich, sieht folgendermaßen aus:
1
Versuch 17: Geometrische Optik/ Mikroskop
Farbe
rot
gelb/orange
grün
blau
violett
Wellenlänge in nm
≈ 750 − 640
≈ 640 − 580
≈ 580 − 500
≈ 500 − 440
≈ 440 − 400
2
Frequenz in THz
≈ 400 − 468
≈ 468 − 517
≈ 517 − 600
≈ 600 − 681
≈ 681 − 749
Zur Berechnung der Frequenz aus der Wellenlänge wird f =
c
λ
verwendet.
Reflexion
Beim Übergang eines Lichtstrahls von einem Medium 1 in ein anderes Medium 2, wird ein Teil
der Intensität reflektiert, der andere Teil tritt in das angrenzende Medium ein. Der einfallende
und der reflektierte Strahl liegen in einer gemeinsamen, senkrecht auf der Grenzfläche stehenden
Ebene, und der Einfallswinkel α ist gleich groß wie der Ausfallswinkel α0 (Abb. 1).
Abb. 1: Reflexion und Brechung an einer Grenzfläche
Die Reflexion lässt sich, wie auch die Brechung und die allgemeine Ausbreitung des Lichts,
mithilfe des Fermatschen Prinzips erklären, welches aussagt, dass ein Lichtstrahl immer den Weg
zwischen zwei Punkten wählt, für den er die kürzeste Zeit benötigt.
Abb. 2: Fermatsches Prinzip
Versuch 17: Geometrische Optik/ Mikroskop
3
Brechungsgesetz
Um den Verlauf der Lichtstrahlen im Medium zu beschreiben wird das von W. Snellius entwickelte
Brechungsgesetz verwendet, welches sagt, dass das Produkt aus Brechungsindex und Sinus des
Strahlenwinkels zur Normalen vor und nach der Brechung gleich sind (siehe Abb. 2).
n2 · sinβ = n1 · sinα
(2)
Zur Herleitung dieses Gesetzes kann das Fermatsche Prinzip herangezogen werden. Hierfür wird
nach der kürzesten Durchlaufzeit t eines Lichtstrahls von Punkt A nach Punkt B gesucht, also:
dt/dx = 0.
Linsen
Linsen sind transparente Körper mit zwei Grenzflächen an denen Brechung stattfindet und deren
optische Achsen zusammenfallen. Hauptsächlich werden Linsen durch die Brennweite charakterisiert. Dabei wird zwischen Sammellinsen (konvex) und Zerstreuungslinsen (konkav) unterschieden. Aus der Abbildungsgleichung lässt sich folgende geometrische Regel aufstellen: Brennpunktstrahlen, Strahlen die durch den Brennpunkt F1 verlaufen, werden beim auftreten auf die Linse
zu Parallelstrahlen, Strahlen die parallel zu optischen Achse verlaufen und Parallelstrahlen werden zu Brennpunktstrahlen, welche durch den Brennpunkt F2 verlaufen. Mittelpunktstrahlen,
Strahlen die durch den Mittelpunkt der Linse verlaufen, werden nicht gebrochen. Der Abstand
des Brennpunktes zur Hauptebene der Linse wird dabei als Brennweite bezeichnet.
Konvexe Linsen: Parallelstrahlen werden so gebrochen, dass sie in einen Punkt zusammen laufen.
Konkave Linse: Parallelstrahlen laufen bei Brechung auseinander.
Abb. 3: Strahlengang an einer Konvexlinse (links) und an einer Konkavlinse (rechts)
Entsteht bei der Abbildung eines Gegenstandes G ein Bild B, welches sich auf der vom Objekt
abgewandten Seite befindet so wird dieses Bild als reell bezeichnet. Befindet sich das Bild auf der
Seite, welche dem Objekt zugewandt ist, so wird dieses Bild als virtuell bezeichnet. Reelle Bilder
lassen sich im Gegensatz zu virtuellen mit einen Schirm auffangen. In Abb. 3 ist zu erkennen, dass
die Strahlen durch die Punkte F1 und F2 verlaufen. Diese werden mit F wie Fokus abgekürzt.
Abbildungsgleichung
Aus der geometrischen Betrachtung dreier Lichtstrahlen, die von einem Gegenstand über eine
Linse auf das Bild abgebildet werden, lässt sich diese Abbildungsgleichung zeichnerisch herleiten.
Die Verhältnisse der Gegenstandsgröße G und der Bildgröße B zu der Gegenstandsweite g und
Bildweite b und der Brennweite der Linse f erschließen sich direkt aus der Anwendung des
Strahlensatzes.
Versuch 17: Geometrische Optik/ Mikroskop
4
Abb. 4: Zeichnerische Konstruktion zur Linsengleichung
Aus der Abbildung folgt:
1
1 1
= +
f
b g
(3)
Dies ist die Abbildungsgleichung für dünne Linsen und achsennahe Strahlenverläufe. Für dicke
Linsen werden beide Hauptebenen der Linse benötigt. Bei dünnen Linsen fallen diese nahezu
zusammen, sodass sie mit einer Ebene angenähert werden können. Für die Brennweite einer
dicken Linse gilt:
1
1
(n − 1) · d
1
= (n − 1) ·
−
+
(4)
f
R1 R2 n · R1 · R2
Abb. 5: Strahlengang an einer dicken Linse
Das Prinzip der Hauptebenen lässt sich auch für Linsensysteme verwenden, es gilt:
1
1
1
d
=
+
−
f
f1 f2 f1 · f2
(5)
Besselsches Verfahren
Für die Bestimmung der Brennweite einer Linse wird häufig das Besselsche Verfahren verwendet.
Dazu wird bei einer optische Bank mit fester Basislänge a, an dem einen Ende der Gegenstand
G und an dem anderem Ende ein Schirm angebracht. Dazwischen wird eine variierbare Linse
positioniert.
Ist der Abstand des Schirms vom Gegenstand größer als das Vierfache der Brennweite, so gibt es
genau zwei Linsenstellungen, bei denen die Linse ein scharfes Bild auf dem Schirm erzeugt. Die
Linse wird zwischen diesen beiden Positionen verschoben und die jeweiligen Gegenstandweiten
g1 und g2 gemessen. Aus der Differenz ergibt sich der Abstand der beiden Linsenpositionen e.
Versuch 17: Geometrische Optik/ Mikroskop
5
Abb. 6: Brennweitenbestimmung mit dem Besselschen Verfahren
Die Brennweite ergibt sich zu:
a2 − e 2
(6)
4·a
Das Besselsche Verfahren hat den Vorteil gegenüber der einfachen Berechnung aus Bild- und
Gegenstandsweite mittels der Linsengleichung, dass bei dicken Linsen oder Linsensystemen die
Lage der Hauptebenen und nicht bekannt sein muss.
Bei einem Linsensystem wird ein beliebiger Bezugspunkt P gewählt an dem die zwei Gegenstandsweiten abgelesen werden. Dadurch lässt sich die Gesamtbrennweite des Systems bestimmen. Mit
f=
Abb. 7: Besselsches Verfahen für ein Linsensystem
diesem Verfahren und der Linsengleichung für dicke Linsen lässt sich so die Brennweite einer
Zerstreuungslinse bestimmen, wenn der Abstand zwischen den Hauptebenen und die Brennweite
der anderen Linse bekannt sind.
Linsenfehler
Chromatische Aberration
Bei Linsen oder Prismen spielt Dispersion eine entscheidende Rolle. Dispersion bezeichnet hier
die Abhängigkeit der Lichtbrechung von der Frequenz des Lichts. Da jeder Farbe des Lichts eine unterschiedliche Frequenz zugeordnet ist, werden diese unterschiedlich stark gebrochen. Dies
ist die Ursache der chromatischen Aberration, welche sich aus dem Griechischen chroma (Farbe)
und aberrare (abschweifen) zusammensetzt. Trifft monochromatisches Licht, d.h. Licht einer Frequenz, auf eine Sammellinse, so laufen alle Strahlen in einem Punkt zusammen. Das gilt jedoch
nicht mehr wenn es sich dabei um Licht verschiedener Farben handelt. Bei weißem Licht, welches aus allen Frequenzen des sichtbaren Bereichs besteht, ist dieser Fehler deutlich zu erkennen.
Durch die unterschiedlich starke Brechung entstehen für die einzelnen Frequenzen unterschiedliche Brennweiten (Abb. 8). Das entworfene Bild eines Gegenstandes von der Linse zeigt dadurch
farbliche Ränder.
Versuch 17: Geometrische Optik/ Mikroskop
6
Abb. 8: Strahlengang bei chromatischer Aberration
Sphärische Aberration
Auch bei monochromatischem Licht können bei der Abbildung von Gegenständen an Linsen Fehler entstehen. Die sphärische Form und die endliche Größe der Linse, beeinflussen das Verhalten
von Lichtstrahlen in Abhängigkeit zum Abstand zur optischen Achse. Es wird dabei zwischen
achsennahen und achsenfernen Strahlen unterschieden. Die Abweichung der Brennweiten nimmt
mit dem Abstand des Strahls zur optischen Achse zu.
Abb. 9: Strahlengang bei sphärischer Aberration
Koma
Bei Koma handelt es sich, im Gegensatz zur sphärischen Aberration, nicht um symmetrisch zur
Symmetrieachse einfallende Lichtbündel, sondern um parallele Lichtbündel, die auf eine schief
gestellte Linse treffen, so entsteht Koma. Der Brechwinkel hängt dabei nicht mehr nur vom
Abstand h zur optischen Achse ab, wie bei der sphärischen Aberration, sondern wird durch
einen weiteren Faktor beeinflusst. Es ist entscheidend ob die Strahlen oberhalb oder unterhalb
des Mittenstrahls verlaufen. Daraus ergibt sich, dass bei der Abbildung eines Punktes A, welcher
sich außerhalb der Symmetrieachse befindet, ebenfalls Koma auftritt. Bei der Abbildung des
Punktes schneiden sich die Strahlen der verschiedenen Teilbündel in den Punkten F15 , F14 ,
F13 , F12 mit unterschiedlichen Abständen zur Symmetrieachse. Die Strahlen verlaufen aufgrund
unterschiedlicher Oberflächenkrümmungen unsymmetrisch durch das optische System. Dadurch
entsteht statt eines scharfen Beugungsscheibchens eine unscharfe Bildkurve.
Astigmatismus schiefer Bündel
Astigmatismus tritt auf, wenn ein Lichtbündel schräg auf die Linse trifft (Abb. 10). Durch den
unsymmetrischen Verlauf zur optischen Achse, entsteht dieser Fehler. Dabei wird zwischen zwei
Arten von Strahlen unterschieden: Die Strahlen in der horizontalen Schnittebene (Sagittalebene)
und die in der senkrechten Schnittebene (Meridionalebene). Da bei schrägem Einfall des Lichts
Versuch 17: Geometrische Optik/ Mikroskop
7
Abb. 10: Strahlengang bei Koma
auf die Linse unterschiedliche lokale Krümmungsradien in den jeweiligen Ebenen auftreten, werden Strahlen der Meridionalebene in einem anderen Bildpunkt, in der Bildweite bM , als Strahlen
der Sagittalebene, in der Bildweite bS , abgebildet. Durch diese unterschiedlichen Brennweiten
erscheint der Bildpunkt in den unterschiedlichen Weiten x1 , bM , x2 , bS oder x3 nicht als Punkt,
sondern in Form zweier Bildlinien und dadurch nicht mehr scharf (Abb. 11).
Abb. 11: Astigmatismus schiefer Bündel
Abb. 12: Abbildung zum Astigmatismus
Mikroskop
Ein Mikroskop besteht im einfachsten Fall aus zwei Linsen L1 und L2 . Die erste Linse ist das
Objektiv und entwirft ein reelles Zwischenbild, welches mit einem Schirm aufgefangen werden
kann. Dieses Zwischenbild des Gegenstandes G befindet sich in der Brennebene der zweiten
Linse dem Okular. Durch das Okular gelangen parallele Strahlenbündel von jedem Punkt des
Gegenstandes ins Auge, sodass ein vergrößertes virtuelles Bild des Gegenstandes im Unendlichen
erscheint. Der Abstand zwischen den beiden Brennebenen der Linsen L1 und L2 wird als optische
Tubuslänge T bezeichnet.
Unter Verwendung des Strahlensatzes und der Linengleichung folgt analog zur Lupe für die
Vergrößerung des Mikroskops:
·b · s0
VM =
(7)
f1 · f2
Versuch 17: Geometrische Optik/ Mikroskop
8
Abb. 13: Strahlengang am Mikroskop
Die Vergrößerung kann auch als Produkt der Einzelvergrößerungen von Objektiv und Okular
geschrieben werden:
VM = VObjektiv · VOkular
(8)
Da F1 sehr klein ist, gilt b ≈ T . Damit kann die Vergrößerung ausgedrückt werden duch:
VM =
s0 · T
f1 · f2
(9)
Abbesche Theorie der Abbildung
Für die Abbildung eines Nichtselbstleuchters spielt Beugung eine entscheidende Rolle. Wird ein
Objekt mit parallelem Licht beleuchtet, so erscheint die nullte Beugungsordnung in Richtung des
durchgehenden Lichts. Jedoch geben erst die höheren Beugungsordnungen Auskunft über den
Abstand. Es gilt:
m · λ = d · sin α
(10)
m: Beugungsordnung (= 1, 2, ...), d: Abstand
Zur Entstehung der Bilder B1 und B2 wird die +1. und die−1. Beugungsordnung benötigt.
Daraus folgt, dass die Objektivlinse L1 des Mikroskops mindestens das Licht der ±1 Beugungsordnung unter dem Winkel θ1 noch erfassen können, d. h. die numerische Apertur NA muss
mindestens:
λ
N A = n · sin α > n · sin θ1 =
(11)
d
sein, um die räumliche Auflösung zu erreichen. Daraus ergibt sich:
d >=
λ
λ
=
n · sin α
NA
(12)
Durch Verwendung von Immersionsöl mit Brechungsindex n lässt sich die Numerische Apertur
vergrößern.
Experiment
Messprinzip
Vor dem Versuch wird auf der Lampe die Kondensorlinse befestigt. Die Lampe wird nun am
Ende der optischen Bank justiert. Der Schirm wird in ca. 100 cm im hinreichendem Abstand zur
Lampe befestigt. Die verwendeten Dias können auf der Kondesorlinse gesteckt werden. Dabei ist
Versuch 17: Geometrische Optik/ Mikroskop
9
Abb. 14: Abbesche Theorie der Abbildung
auf eine gute Beleuchtung des Dias zu achten. Dazu wird die Glühwendel so dicht wie möglich
ans Dia heran geschoben.
Zur Auswertung soll zu allen Versuchsteilen, bei denen eine Brennweite bestimmt werden soll,
zusätzlich zum Besselschen Verfahren die Brennweite graphisch bestimmt werden. Hierzu wird
jeweils der Mittelwert aus den fünf Messungen für die Bildweite auf die eine Achse mit den
dazugehörigen Mittelwert für die Gegenstandsweite auf der anderen Achse verbunden. Aus der
Abbildungsgleichung folgt, dass alle Geraden und die Winkelhalbierende des ersten Quadranten
sich in einem Punkt schneiden. Dieser Schnittpunkt entspricht der Brennweite, welche sowohl
auf der x-Achse als auch auf der y-Achse abgelesen werden kann. Da sich die Geraden durch
Ableseungenauigkeiten in der Praxis nicht in einem Punkt treffen, werden die Schnittpunkte
sowohl auf der x-Achse als auch auf der y-Achse abgelesen. Aus allen Werten ist der Mittelwert
zu bilden.
Abb. 15: Graphische Bestimmung der Brennweite
Versuch 17: Geometrische Optik/ Mikroskop
10
Vorbereitende Aufgaben
Leiten sie das Snelliussche Brechungsgesetz aus dem Fermatschen Prinzip her.
Leiten sie die Abbildungsgleichung mithilfe des Strahlensatzes her.
Leiten Sie die Winkelvergrößerung des Mikroskops her.
1. Bestimmung der Brennweite an Sammellinsen
Mit dem Besselschen Verfahren ist die Brennweite für eine frei wählbare Sammellinse zu bestimmen. Die Position des Gegenstands, das Pfeildia, ist dabei abzuschätzen. Für die Bestimmung
sollen bei mindestens 2 verschiedenen Abständen zwischen Schirm und Gegenstand die Stellungen der Linse gemessen werden, an denen eine scharfe Abbildung des Pfeildias entsteht. Für jeden
Abstand sind die Positionen für Verkleinerung und Vergrößerung jeweils fünfmal zu messen. Dabei bietet es sich an jeweils fünfmal die Position der Vergrößerung und anschließend fünfmal die
Position der Verkleinerung zu messen. Aus den gemessenen Werten sind mit:
a2 − e 2
(13)
4·a
die Brennweiten zu bestimmen. Dabei ist zu beachten, dass die Pfeile bei der Verkleinerung sehr
klein sind und dadurch schwer zu erkennen. Zu jedem Wert gehört eine Fehlerrechnung!
Warum muss der Abstand a beim Besselschen Verfahren mindestens das Vierfache der Brennweite betragen damit zwei scharfe Abbildungen entstehen?
f=
2. Bestimmung der Brennweite eines Linsensystems
Die Brennweite einer Zerstreungslinse soll bestimmt werden. Dazu wird zunächst die Gesamtbrennweite des Linsensystems bestimmt. Die Brennweite der Sammellinse beträgt 50 mm und
der Abstand d zwischen beiden Hauptebenen 2 cm. Aus diesen Werten lässt sich die Brennweite
aus der Gleichung:
1
1
1
d
=
+
−
f
f1 f2 f1 · f2
(14)
bestimmen. Für das Bestimmen der Gesamtbrennweite f wird wie im Versuchsteil eins vorgegangen.
Warum kann die Brennweite einer Zerstreuungslinse nicht so bestimmt werden wie bei Sammellinsen?
Wie groß muss die Brennweite der Sammellinse sein, damit die Brennweite der Zerstreuungslinse
bestimmt werden kann?
3. Chromatische Aberration
Zunächst wird mit der Linse 2 das Spaltdia scharf abgebildet. Nun wird der Schirm verdreht,
sodass die Lichtstrahlen unter einen Winkel von ca. 20◦ auf den Schirm treffen. Jetzt soll das
entstandene Bild beschrieben werden. Es entstehen farbliche Ränder, die durch chromatische
Aberration erklärt werden können.
Anschließend ist das Verhältnis zwischen Brechung und Farbe zu untersuchen. Hierzu werden
die Farbfilter, die Linse 2 und das Pfeildia benötigt. Zwischen Gegenstand und Linse wird ein
Farbfilter positioniert und anschließend für jede Farbe für mindestens 2 verschiedene Abstände
Versuch 17: Geometrische Optik/ Mikroskop
11
die Brennweite ermittelt. Hierfür wird wie im Versuchsteil 1 das Besselsche Verfahren verwendet
und ebenfalls fünfmal die Gegenstandsweite für Vergrößerung und Verkleinerung gemessen. Vergleichen Sie die Brennweite für die einzelnen Farbfilter.
Welche Auswirkung hat die chromatische Aberration auf die Abbildung?
4. Sphärische Aberration
Zur Untersuchung der sphärischen Aberration ist der Abstand zwischen Gegenstand und Schirm
zu verkleinern. Das Verhältnis zwischen Brechung und Achsenabstand ist zu ermitteln. Dazu
wird als Gegenstand ein Gitterdia verwendet. Mithilfe der beiden Blenden, die an die Linse 2
angebracht werden können, kann das Verhalten von achsennahen und achsenfernen Strahlen unabhängig voneinander untersucht werden. Hierzu ist wie in den Versuchsteilen zuvor vorzugehen
und die Brennweite für achsennahe und achsenferne Strahlen zu ermitteln.
Welche Auswirkung hat die sphärische Aberration auf die Abbildung?
5. Koma
Für diesen Linsenfehler wird das Lochdia mit regelmäßigen Abständen verwendet. Für die Linse
2 soll das Bild betrachtet und die Form der Punkte am Rand und in der Mitte diskutiert werden.
Anschließend verdrehen Sie die Linse um ca. 20◦ . Begründen Sie ihre Beobachtungen.
Welche Auswirkung hat Koma auf die Abbildung?
6. Mikroskop
In diesem Versuchsteil ist ein Mikroskop, mit einer mindestens zwanzigfachen Vergrößerung aus
den vorhandenen Linsen zusammenzusetzen. Als Gegenstand soll das Dia mit der Mikrometerskala verwendet werden. Das reelle Zwischenbild wird mit dem Schirm aufgenommen und der
Lupe betrachtet. Klemmen Sie zur Betrachtung des Zwischenbildes eine Milimeterskala an den
Schirm, damit Sie die Größe des virtuellen Bildes abschätzen können. Dazu betrachten Sie das
Bild in deutlicher Sichtweite (25 cm) entfernt vom Schirm.
Messen Sie für drei verschiedene Gegenstands- und Bildweiten die jeweilige Vergrößerung.
Welche Linse wurde als Objektiv verwendet und welche als Okular? Begründen Sie diese Auswahl.