Kapitel 2

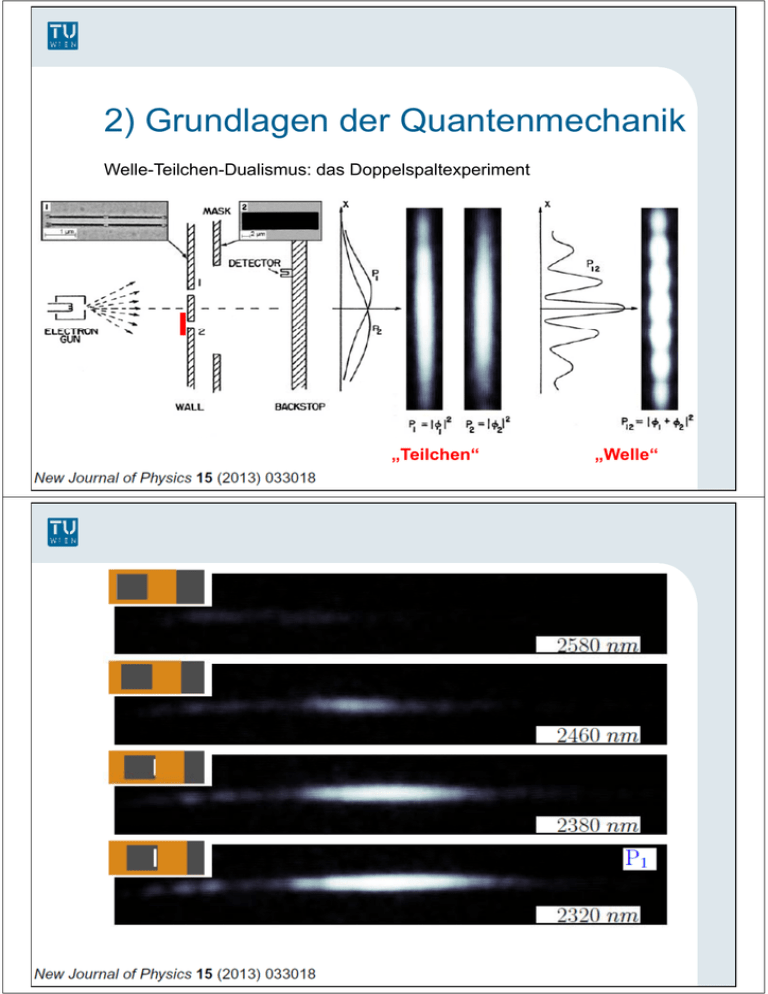
2) G
Grundlagen
dl
d
der Q
Quantenmechanik
t
h ik
Welle Teilchen Dualismus: das Doppelspaltexperiment
Welle-Teilchen-Dualismus:
„Teilchen“
„Welle“
Durch welchen Schlitz ist das Teilchen geflogen?  Beobachtung
Welle-Teilchen-Dualismus:
1) P = ||2
 ... „Wahrscheinlichkeitsamplitude“
2) mehrere alternative Wege: P = |1+...+n|2
3) B
Beobachtung
b ht
entlang
tl
d
der W
Wege: P =P
P1+...+P
Pn
Heisenberg‘sche Unschärferelation:
Ist der Ortes eines Teilchens bis auf eine Messungenauigkeit x genau
bekannt,
be
a t, ist
st es u
unmöglich,
ög c , de
den Impuls
pu s desse
desselben
be Teilchens
e c e s ge
genauer
aue a
als
s
h/p zu bestimmen (und umgekehrt).
Nobelpreis 1932
Werner Karl Heisenberg
g
The Nobel Prize in Physics 1932 was awarded to Werner Heisenberg
"for the creation of quantum mechanics, the application of which
has, inter alia, led to the discovery of the allotropic forms of
y
g
hydrogen".
Abschätzung der Größe eines Wasserstoffatoms
Annahme: x = a  p = h/a
kinetische Energie eines Elektrons mit Impuls p:
Ekin 
p2
h2

2m 2ma 2
potentielle Energie eines Elektrons im Abstand x vom Kern: E pot  
Minimierung der Gesamtenergie Eges

h2
e2


0
da
ma 3 a 2
dEges

h2
e2


2ma 2 a
h2
 0.528 Å
a0 
me 2
De Broglie-Hypothese
Broglie Hypothese (Doktorarbeit 1923)
Zuordnung von Wellencharakter zu Bewegung von Teilchen
Klassische Physik
mev
Quantenmechanik

mev 2
kinetische Energie


Teilchenimpuls
1
2
pe

Ee


h

k

Wellenlänge der Teilchenbewegung

Frequenz der Materiewelle
Elektromagnetische Strahlung
Welle, E-, B-Feld
Teilchen (Photonen)
E ph  ;
pph  E ph  c   k 
h

e2
a
Nobelpreis 1929
Prince Louis-Victor Pierre Raymond
y
de Broglie
g
The Nobel Prize in Physics 1929 was awarded to Louis de Broglie "for
his discovery of the wave nature of electrons".
Davisson Germer Experiment
Davisson-Germer-Experiment
Davisson and Germer, Phys.Rev. 30, 705 (1927)
Nobelpreis 1937
George Paget Thomson
Clinton Joseph
p Davisson
The Nobel Prize in Physics 1937 was awarded jointly to Clinton
Joseph Davisson and George Paget Thomson "for their
experimental discovery of the diffraction of electrons by
y
crystals".
Low Energy Electron Diffraction (LEED)
pe  mev  h     h mev
de Broglie
g Wellenlänge:
g
1
Ee  mev 2  v  2Ee me
2
Å  150 Ee [eV]
Abschätzung:  [Å]
Bragg Reflexion
Bragg-Reflexion
Bedingung für Reflexion
g
der Streuung
g von
aufgrund
zwei Kristallebenen:
2d sin   n 
Lösungen nur für d < /2
 Filter für langsame
(langwellige) Teilchen
senkrechter Einfall:


2

2d  n

n  kd 
d
p

Elektronenmikroskopie
ersetze Lichtwellen durch Elektronenwellen
Transmission (TEM)
Reflexion (REM)
 [Å]  150 15000[eV]  0.1 Å
Nobelpreis 1986
Ernst Ruska
The Nobel Prize in Physics 1986 was divided, one half awarded to
Ernst Ruska "for his fundamental work in electron optics, and for
the design of the first electron microscope".
Die Schrödingergleichung
keine Ableitung möglich  „Erraten“ der Schrödinger-Gleichung
Quantenmechanik: Welle – Teilchen – Dualismus
Unbestimmtheitsrelation
de Broglie Hypothese
eines Teilchens
p 2 (  k )2
E

2m
2m
Energie einer Welle
E  
Impuls bekannt  Ort vollständig unbestimmt
„Materiewelle“:  ( x  t )  A  e i ( kx t )
Verwendung von Operatoren  „Frage
Frage“ an System
 Frage nach Energie: Ê    , Frage nach Impuls: p̂  k 
Darstellung für E:

 ( x  t )   i   ( x  t )
t

E Welle  ( x  t )    ( x  t )   i  t  ( x  t )
Darstellung für p:

 ( x  t )  ik  ( x  t )
x


p  ( x  t )  k  ( x  t )   i  x  ( x  t )
 2  2 
p2
2 k 2
ETeilchen ( x  t )  T ( x  t ) 
 ( x t ) 
 ( x t )   
 ( x t )
2 
2m
2m
 2m x 
Gleichsetzen der Ausdrücke für E 
Schrödingergleichung für freies Teilchen

 2 2 
E  ( x  t )   i  t  ( x  t )   
 x   ( x t )
 2m 
Nobelpreis 1933
Paul Adrien Maurice Dirac
Erwin Schrödinger
g
The Nobel Prize in Physics 1933 was awarded jointly to Erwin
Schrödinger and Paul Adrien Maurice Dirac "for the discovery of
new productive forms of atomic theory".
Real und lokal?
Information verbreitet sich maximal mit Lichtgeschwindigkeit
g
g
Teilchen hat Eigenschaft, auch wenn es nicht beobachtet wird
I  I0 cos2 
Zufall oder
Unkenntnis?
Jan-Markus Schwindt, Tutorium Quantenmechanik
Bell‘sche
Bell
sche Ungleichung
mehrere Eigenschaften in Korrelation gemessen  p( A, B )  p( A,C )  p(B, nC )
z.B. drei Richtungen von Polarisationsfiltern; gleichzeitige Messung durch
Verwendung „verschränkter“ Photonen
Messung
g liefert:
1
1
1
cos2 AB  cos2 AC  sin2 BC
2
2
2
3 1 1
AB  BC  30; AC  60 
 
4 4 4
 Aufgabe von Realität oder Lokalität
Jan-Markus Schwindt, Tutorium Quantenmechanik
Born‘sche
Born
sche Wahrscheinlichkeitsinterpretation
nur rechnerische Größe
[ , x+dx]] zu finden
Wahrscheinlichkeit,, das Teilchen im Intervall [x,
P ( x  t ) dx    ( x  t ) 2 dx


Verallgemeinerung in 3D: P (r  t ) d 3r    (r  t ) 2 d 3r
[ x  x  dx ]
Aufenthaltswahrscheinlichkeit des Teilchens im Volumen [ y  y  dy ]
[ z z  dz ]

 2
  ( r  t )   Wahrscheinlichkeitsdichte
 Bestimmung der Normierungskonstanten aus Forderung

 2
3
3
d
r
P
(
r
)

d
r


(
r
) 1


V
V