Resonanz - HAW Hamburg
Werbung

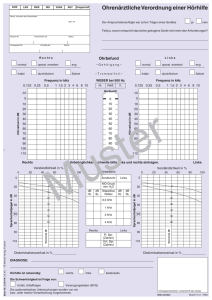
Department Informations- und Elektrotechnik Labor für Grundlagen der Elektrotechnik Studiengruppe: Protokollführer (Name, Vorname): ETP2 Übungstag: Professor: Weitere Übungsteilnehmer: Testat: Resonanz Übersicht In diesem Labor werden Sie Resonanzkurven, Bandbreiten und Gütefaktoren experimentell bestimmen. Dazu nehmen Sie im ersten Teil der Übung Messungen an einem Serienresonanzkreis unter verschiedenen Betriebsbedingungen durch. Zusätzlich werden Sie erfahren, wie Sie die Güte des Kreises durch Impedanzentkopplung des Generatorinnenwiderstands mit einem zwischengeschalteten Impedanzwandler nach Angabe des Betreuers optimieren können. Im zweiten Teil werden Schaltvorgänge an diesem Schwingkreis dargestellt und Sie erfassen das Einund Ausschaltverhaltens des Schwingkreises bei periodischer Rechteck-Impulsanregung. Theoretische Grundlagen RLC-Resonanzkreise: Resonanzfrequenz, Bandbreite, Phasengang, Schwingungswiderstand, Güte Schaltvorgang eines Schwingkreises: gedämpfte Schwingung, Kriechverhalten, aperiodischer Grenzfall Vorbereitung Wiederholen Sie die Themen RLC-Resonanzkreise und beachten Sie dazu auch den Anhang zum transienten Verhalten eines Schwingkreises Gegeben sei eine Reihenschaltung einer Luftspule mit einer Induktivität von L = 100mH und einem Gleichstrom-Drahtwiderstand RL = 10. Der verwendete Sinus-Generator habe einen Innenwiderstand (load impedance) Ri = 50. a) Berechnen Sie die erforderlichen Kapazitäten C für einen Serienresonanzkreis bei folgenden Resonanzfrequenzen: f = 100 Hz, f = 500 Hz, f = 1 kHz und zusätzlich auch für die beiden höheren Frequenzen f = 5 kHz und f = 10 kHz. Anmerkung: Die gegebenen Spulendaten sind nur gültig für Frequenzen f < 1 kHz. b) Berechnen Sie die zugehörigen Gütefaktoren Q und Bandbreiten f (in Hz) mit dem Gesamtverlustwiderstand Ri + RL und mit dem Spulen-Drahtwiderstand RL allein. 1(3) Version 1.01 Laborversuche 1. Resonanz - Eingeschwungener Zustand Bauen Sie eine Serien–Resonanzschaltung unter Verwendung eines Generators, einer Präzisions- CDekade, einer Luftspule und eines Oszilloskopes nach Abb.1 auf. Geben Sie dabei Generator, CDekade und Oszilloskop einen gemeinsamen Massepunkt. Stellen Sie am Funktionsgenerator eine SinusAmplitude ûGen = 1 V ein. ûGen = 2Vpp Beachten Sie: Bei der Amplitudeneinstellung ist darauf zu achten, dass „load: hiZ“ gewählt ist, nur dann wird der korrekte Wert der internen Spannungsquelle ûGen angezeigt. Der Generator verfügt über einen Innenwiderstand von Ri = 50 . 1.1 Bestimmen Sie durch Messung von ûc / ûGen punktweise den Amplitudengang für die Resonanzfrequenzen 500 Hz und 1 kHz. Die Frequenzen sind dabei im Bereich der Resonanzfrequenz der vorausberechneten Bandbreite zu variieren. An der Resonanzstelle sind die Messpunkte hinreichend eng zu setzen. Beachten Sie, dass ûGen die eingestellte, interne Spannung des Signalgenerators vor dem Innenwiderstand ist. 1.2 Stellen Sie die Ergebnisse als Funktion der Frequenz dar. 1.3 Bestimmen Sie die Bandbreiten f (in Hz) und die Gütefaktoren Q (= ûc / ûGen bei Resonanz). 1.4 Wiederholen Sie 1.1 bis 1.3 mit weitgehend abgekoppeltem Generatorinnenwiderstand, indem nach Einweisung ein Operationsverstärker-Impedanzwandler zwischen Generator und Spule/CDekade geschaltet wird. Dazu reduzieren Sie die Generatorspannung etwa soweit, dass keine Verzerrungen des Signals bei Resonanz erkennbar werden (typisch: 300 mVpp). Beachten Sie: Der 0V-Anschluss der 15V-Versorgungspannung des Operationsverstärkers ist mit Masse zu verbinden. 1.5 Vergleichen Sie die so optimierten Bandbreiten und Gütefaktoren mit den vorherigen Ergebnissen. 2(3) Version 1.01 1.6 Erhöhen Sie unter Beibehaltung der Schaltung mit Operationsverstärker durch Anpassung von C nun die Resonanzfrequenzen auf 5 kHz bzw. 10 kHz und berechnen Sie aus den Gütefaktoren die bei diesen Frequenzen wirksamen (durch Wirbelströme deutlich höheren) Spulenverlustwiderstände. Beachten Sie dazu auch den geometrischen Wicklungsaufbau der Spule. 2. Resonanz - Schaltverhalten Für diese Messungen wird der Impedanzwandler zwischen Generator und Spule/C-Dekade wieder entfernt und durch eine Präzisions-Widerstandsdekade ersetzt, mit der die Gesamtdämpfung des Kreises aus Abb.1 stark erhöht werden kann. Stellen Sie die Kreisresonanz mit der C-Dekade auf f = 1 kHz fest ein. Zur Schaltanregung wählen Sie am Generator ein periodisches ûGen = 1,0V-Rechteckimpulssignal mit niedrigerer Frequenz. Am Oszilloskop sollen die Zeitfunktionen der Kondensatorspannung nach den beiden Schaltflanken in einem Oszillogramm dargestellt werden. 2.1 Stellen Sie gedämpfte Schwingungen aus 5-10 Perioden dar und bestimmen Sie daraus das Dämpfungsmaß (s. Anhang, Abb.2). Bestimmen Sie - grafisch (mittels Cursor) - die (Kreis)Frequenz D der gedämpften Schwingung und vergleichen Sie mit dem vorausbestimmten Wert r (ungedämpfter Fall). 2.2 Erhöhen Sie nun schrittweise die Dämpfung bis zum Erreichen der Aperiodizität. Speziell soll genau der aperiodische Grenzfall eingestellt werden. Anhang Transientes Verhalten eines Schwingkreises Aus dem Amplitudenverhältnis aufeinanderfolgender Schwingungsberge der gedämpften Schwingungen lässt sich zusammen mit der Periodendauer Td das Dämpfungsmaß „“ des Schwingkreises aus der Messung ermitteln: y δ Td ln i y i 1 T wird auch als „logarithmisches Dekrement“ bezeichnet und mit bezeichnet: = Td. Yi stationärer Zustand Yi+1 t Gemäß Theorie ist =R/2L. 3(3) Version 1.01