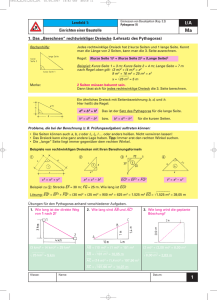
Das rechtwinklige Dreieck
Werbung

Flächensätze im rechtwinkligen Dreieck Teil 1 Satz des Pythagoras Ein stumpfwinklige s Dreieck Ein spitzwinkliges Dreieck Ein rechtwinklige s Dreieck Rechtwinklige Dreiecke Das rechtwinklige Dreieck Kathete 2 Kathete 1 Hypotenuse Im rechtwinkligen Dreieck gilt: Die Summe der Kathetenquadrate ist gleich dem Hypotenusenquadrat kurz: K1² + K2² = Hyp² C C C Hyp K2 a b A c K1 B K1 K1 K2 b A Hyp a Hyp c a b B A K2 c B K1² + K2² = Hyp² K1² + K2² = Hyp² K1² + K2² = Hyp² c² + a² = b² a² + b² = c² b² + c² = a² Pythagoras - seinerzeit in grandioser Mathematiker- wurde um 570 vor Christus in Spermos auf der griechischen Insel Samos geboren. Pythagoras verbrachte seine Kindheit mit seinen zwei Brüdern auf Samos. Seine Lehrer waren Philosophen, die sein Leben maßgeblich beeinflussten. Sie waren es auch, die ihm die Welt der Mathematik öffneten. Um 535 vor Christus flüchtete Pythagoras nach Ägypten. In Dispolis gewährte man ihm die Mitgliedschaft in der Priesterschaft. 520 vor Christus kehrte Pythagoras nach Samos zurück. Aber diese Rückkehr sollte nicht lange dauern, denn zwei Jahre später verließ er die Insel wieder und ging nach Crotone in Italien. Dort gründete er eine philosophische und religiöse Gemeinschaft, die dort sehr beliebt war. Pythagoras war der Vorsitzende dieses "Inneren Ordens", der als Mathematikoi bezeichnet wurde. Die Mathematikoi hatten keine personellen Besitztümer und waren Vegetarier. Die Mitglieder des Inneren Ordens wurden von Pythgaros persönlich gelehrt und befolgten strikt die Regeln des Ordens. Über Pythagoras' Arbeit in diesem Orden ist heute nicht viel bekannt, man weiß nur, dass dieser Orden sich ausschließlich mit Mathematik befasste. Das wohl bekannteste Werk von Pythagoras ist der "Satz des Pythagoras". Pythagoras starb ca. 475 vor Christus . Man kennt das ja, oftmals denkt man sich beim Lernen bestimmter Dinge: "Wozu brauche ich das eigentlich, wozu lerne ich das?" Gerade bei der Mathematik sieht man oft in verzweifelte Gesichter. Der Satz des Pythagoras wird heute noch häufig zum Abstecken rechter Winkel benutzt. In einigen handwerklichen Berufen, z. B. bei Baufacharbeiten gehört die Konstruktion eines rechten Winkels zu den Grundkenntnissen. Hier eine Beispielaufgabe! Ein Haus liegt an einem See. Am anderen Ufer steht ein Baum. Der Hausbesitzer will die Entfernung zwischen Haus und Baum bestimmen. Dazu entfernt er sich vom Haus in östlicher Richtung bis er den Baum unter einem Sehwinkel von 90° sieht. Diese Stelle markiert er mit einer Fahne. Die Entfernung zwischen Fahne und Haus beträgt 450 m. Anschließend misst er die Entfernung der Fahne vom Baum. Diese beträgt 600 m. 600 m 450 m C ges.: b = geg.: c = 450 m a = 600 m b Hyp K2 a K1² + K2² = Hyp² c² + a² = b² b² = c² + a² b= A K1 c B c a 2 b= 2 450 600 2 2 b = 750 Das Haus ist 750 m vom Baum entfernt. erstellt im Rahmen der Intel-Fortbildung von