schematisch

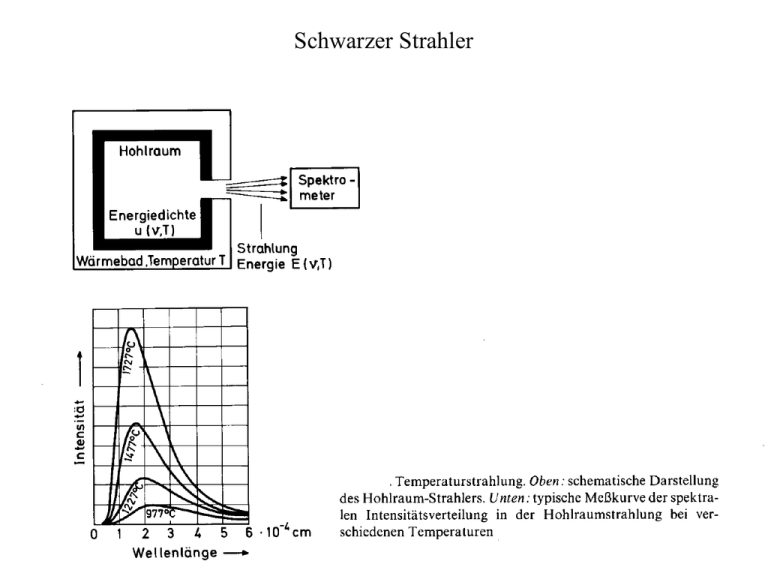
Schwarzer Strahler
Maximum verschiebt sich mit wachsendem T zu kürzeren Emissionswellenlängen

lmax·T = const. = 0,2898 cm·K
Man erhält zum Beispiel:
Wiensches Verschiebungsgesetz
T = 6000 K (Temperatur auf der Sonnenoberfläche)
 lmax = 480 nm (grünes Licht)
Interessant: Empfindlichkeit des Auges in diesem Bereich
am größten.
Zurück zur Hohlraumstrahlung:
Man erhält auf Basis der klassischen Physik:
8n 2
u (n , T )  3 kT
c
Rayleigh-Jeanssche Strahlungsformel
Herleitung entweder durch: 1) Energieinhalt der Moden eines Hohlraumresonators
2) Dimensionsbetrachtung
Energie
[u (n , T )] 
Frequenz Volumen
Kann nur abhängen von n und T und den Naturkonstanten k und c!
Andere Größen kommen nicht in Frage, da die Hohlraumstrahlung
materialunabhängig ist.
Mit n, T, k,und c kann man u(n,T) mit obiger Dimension nur aufbauen mit:
n 2 kT
c3
bis auf einen Zahlenfaktor identisch mit der Rayleigh-Jeans-Formel
8n 2
u (n , T )  3 kT
c
ist aber offensichtlich falsch, da die Energiedichte bei hohen
Frequenzen immer weiter ansteigt (UV-Katastrophe)
u(n,T)
Rayleigh-Jeans
gemessen

n
Außerdem: Die Integration über n 2 dn   liefert eine unendlich große Energiedichte.
0
MaW: Der gemessene Verlauf wird im Rahmen der klassischen Physik nicht richtig wiedergegeben!
Es wird keine UV-Katastrophe beobachtet.
Aber: Im Bereich niedriger Frequenzen stimmt die Formel mit den Beobachtungen überein.
 Es muss einen Mechanismus geben, der die Strahlungsdichte bei hohen Frequenzen (kurze
Wellenlängen) unterdrückt.
 Vorschlag von W. Wien: Einführung eines Expotentialfaktors
Später zeigt sich, dass der Exponent eine neue Naturkonstante enthält.
XI. Licht als Teilchenstrahlung
Wechselwirkung von Licht mit Materie lässt sich in vielen Einzelheiten qualitativ sehr gut im
Rahmen der Maxwell’schen Theorie (Licht als elektromagnetische Welle) beschreiben.
Aber: andere Phänomene bleiben unverständlich wie
 Hohlraumstrahlung
 Obere Grenzfrequenz bei Röntgenstrahlung
Man braucht also ein neues Konzept: a) Quantelung der Schwingungsenergie
b) Beschreibung von Licht als Teilchenstrahlung
Es gibt Lichtpartikel = Photonen = Lichtquanten
XI.1 Wärmestrahlung und gequantelte Schwingungsenergie
Plancksche Strahlungsformel
1898-1900 gelang es Lammer und Pringsheim sowie Rubens und Kurlbaum das Spektrum der
Hohlraumstrahlung mit hoher Präzision zu messen.
Max Planck fand empirisch für den Verlauf von u(n,T) folgende Formel:
8n 2
u (n , T )  3
c
hn
e
hn
kT
Planck’sche Strahlungsformel
1
Diese gibt den experimentellen Verlauf perfekt wieder!
h = neue Naturkonstante der Dimension
[h] = Energie · Zeit
h = Planksches Wirkungsquantum
NB: in der Mechanik werden Größen
der Dimension Energie mal Zeit als
„Wirkung“ bezeichnet
Das Anpassung der Formel an die experimentellen Messwerte liefert:
h = 6,6256·10-34 Js
= 4,135 · 10-15 eVs
Aber: empirische Formel ist für einen Theoretiker unbefriedigend.
Deshalb sucht Planck nach einer theoretischer Begründung der Formel.
Dies gelingt, wenn man annimmt, dass die Oszillatoren auf Wänden des Hohlraums nicht beliebig
schwingen, sondern:
nur mit solchen Amplituden,
dass Schwingungsenergie E
bestimmte Werte annimmt:
also: En = nhn mit n = 0,1,2,3
Die mittlere Energie eines Oszillators ist dann:
hn
E
e
hn
kT
1
= Energie einer Eigenschwingung des Strahlungsfeldes.
Das ist aber total verschieden von dem bekannten
E  kT
Betrachtung von Sonderfällen zeigt:
Für hn « kT  Plancksche Formel geht in Rayleigh-Jeans-Gesetz über
hn
Für hn  kT  Faktor
e
hn
kT
1
sorgt für Unterdrückung der hohen Frequenzen.
 thermische Energie kT reicht nicht aus, um hochfrequente Oszillatoren anzuregen
 hohe Frequenzen kommen im Spektrum nicht vor
Wichtiger Punkt: Planck’sche Formel enthält andere Strahlungsgesetze
z.B.
 Integration liefert Stefan-Boltzmann-Gesetz
Energiedichte im Hohlraum:
u
n
  u (n , T )dn
8 5 k 4 4

T
3 3
15c k

Stimmt mit experimentellem
Wert überein.
 Differenzieren ergibt für Maximum der Kurve und somit das Wiensches Verschiebungsgesetz
Tlmax = 2,898 · 10-3 m·K
Ebenfalls Übereinstimmung mit Experiment
Info:
In der Festkörperphysik (Physik V) wird ausführlich behandelt, dass
Quantelung der Schwingungsenergie eine allgemeine Eigenschaft atomarer Oszillatoren ist.
Das elektromagnetische Spektrum. Bereiche und Einheiten
XI.2 Lichtquanten
Einstein knüpfte weitere kühne Folgerung an die Theorie der Hohlraumstrahlung:
Elektromagnetische Strahlung selbst existiert nur in Form von Energiequanten
Ist n die Frequenz der Welle, ist die Größe eines Energiequanten
E = hn
Dies war zu der Zeit eine revolutionäre Behauptung und sie führte zu gewaltigen Schwierigkeiten.
Z.B. Wie kann man logisch mit „Dualismus“ Welle/Teilchen fertig werden?
Einstein: mit E = hn lassen sich sonst unverständliche Phänomene wie der Photoeffekt
(photoelektrischer Effekt) deuten
Photoeffekt
d.h: aus Atom oder Metalloberfläche wird ein Elektron herausgelöst
 im Rahmen des Wellenbildes wurde erwartet, dass:
Die Elektrische Feldstärke der Welle eine Kraft auf das Elektron bewirkt, die zur Abtrennung des
Elektrons führen kann. Quantitativ kann Effekt aber auf diese Weise nicht erklärt werden.
Grund:
Experimentell zeigt sich, dass die Elektronen die Metalloberfläche mit einer Geschwindigkeit verlassen,
die nicht von der Intensität der Welle, d.h. der Amplitude des elektrischen Feldes abhängt
Experimentell bestätigt wurde, dass ein Maximalwert v0 für die Elektronengeschwindigkeit existiert
Dieser Wert kann mit der Gegenfeldmethode bestimmt werden.
Prinzipskizze:
Auffangelektrode negativ gepolt, d.h. nur Elektronen mit der Energie me/2v²  eU tragen zu Strom I bei.
Ergebnisse:
1) Stromstärke I ist proportional zur Intensität der Strahlung.
2) v0 von Intensität unabhängig
 im klassischen Bild unverständlich, da die auf die Elektronen wirkende Kraft – die elektrische Feldstärke
der entfallenden Welle – mit steigender Intensität wächst!
Aber: Photoeffekt ist leicht mit Lichtquantenhypothese erklärbar:
hv = Energie der Photonen wird als Ganzes auf das Elektron übertragen!
Bindungsenergie der Elektronen: EB
Bindungsenergie bei Metallen = Austrittsarbeit: 
 für die kinetische Energie der freigesetzten Elektronen gilt:
me 2
v0  hn  
2
Die obige einfache Anordnung ermöglicht die Prüfung dieser Beziehung
 man erwartet wegen eU0  v0²·me/2 = hn- eine lineare Beziehung zwischen U0 und n.
Wichtig: Steigung der Geraden muss den Wert für h ergeben, der mit dem aus der
Hohlraumstrahlung bestimmten Wert übereinstimmt.
Dies wurde später experimentell bestätigt.
Bis dahin galt die Hypothese der „Lichtquanten“ als absurd.
Lichtquanten und Röntgenstrahlung
Die Formel für Photoeffekt wurde auch durch Anwendung im Bereich der Röntgenstrahlung quantitativ
bestätigt:
Ekin = hn - EB
Mit dieser Formel kann man unterschiedliche Experimente durchführen:
1) Ist EB bekannt und wird die kinetischen Energie Ekin gemessen.
 Spektroskopie von Röntgen- und Gamma-Strahlen
2) Ist Photonenenergie hn bekannt und wird die kinetischen Energie Ekin gemessen.
 Bestimmung von EB
 chemische Analyse möglich
Heute: ESCA = Electron Spectroscopy for Chemical Analysis
ESCA ist ein mächtiges Instrument in der Oberflächenforschung
Quantenhafte Struktur elektromagnetischer Strahlung manifestiert sich im Röntgenbereich aber auch durch:
Eine obere Grenzfrequenz im Röntgenspektrum
Einfache Erklärung: Elektronen erreichen Anode mit Energie eU; mit U = Röhrenspannung
 es können nur Röntgenquanten mit hn  eU erzeugt werden
 ngr = eU/h
Das heißt: durch Messung von ngr kann man h bestimmen!
Das Experiment dazu ergibt, dass der Wert mit dem aus Photoeffekt und Wärmestrahlung übereinstimmt.
Abschließender Beweis für Existenz des Photons durch Comton-Effekt.
Comton-Effekt:
 Bei Streuung monochromatischen Röntgenlichts können im Streulicht mittels
Drehkristallspektrometer zwei Linien nachgewiesen werden:
1) Linie mit l des einfallenden Lichts
2) Linie l´, die zu längeren Wellenlängen hin verschieben, Betrag hängt vom Streuwinkel ab
Man findet experimentell:
l´ l  const (1-cosJ)
Compton interpretierte den Effekt als Streuung masseloser Teilchen, nämlich der Photonen, an Elektronen:
Photon mit Energie E = hn hat im Rahmen dieser Interpretation den Impuls p = h/l
Experiment bestätigt diese Deutung und liefert für die Konstante in der Formel l´ l  const (1-cosJ)
den Wert const.
hc
me c 2
in Übereinstimmung mit Experiment.
Man beachte: Oft auch l´- l = const (cosJ/2), dann ist die Konstante 2h/mec
Zum Compton-Effekt
XI.3 Energiestufen des Atoms
Lichtemission und Absorption in vielen Aspekten durch Modelle klassisch gebundener Elektronen erklärbar.
Aber: Ordnungsprinzip der Spektrallinien bzw. der Spektren blieb bisher offen.
Wichtiger Schritt zum Verständnis der Atomspektren:
Ritz´sches Kombinationsprinzip:
Lichtfrequenzen eines Spektrums kann man einem Termschema zuordnen, mit dem man die
Frequenzen aller Linien als Differenz zweier Spektralterme darstellt.
nnm = nn-nm
Für Ritz´sches Kombinationsprinzip: Umrechnen auf Energie: 1215,7 Å  10,199885 eV und
1225,7 Å  8,310447 eV. Differenz aus beiden entspricht: 1,8894 eV  6562,8 Å
Noch einmal
schematisch:
E3
n31
n32
n20
E2
E1
n10 n20
n30
n10 n20
n30
Eo
Emissionslinie
Absorptionslinie
Deutung durch Nils Bohr
 Spektralterme ni sind Energiestufen Ei im Atom
Und damit aus nnm = nn-nm die Bohrsche Frequenzbedingung:
Unterster Term: E0 = Grundzustand
Übrige Terme: angeregte Zustände
hn nm  En  Em
} des Atoms
 Absorptionsspektren: es werden bevorzugt Linien betrachtet, die vom Term Eo ausgehen.
Ursache: Atom befinden sich gewöhnlich im Grundzustand!