vorlesung9

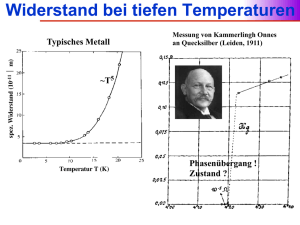
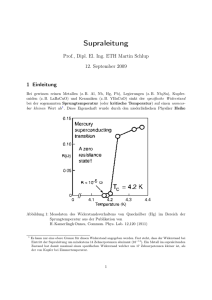
Supraleitfähigkeit
Elektrischer Widerstand
r
Die Sprungtemperatur
(kritische Temperatur)
ma  Tc  const.
Reines Metall
 ist eine Materialkonstante
(Isotopieverschiebung der
Sprungtemperatur)
Tc
Metall mit
Verunreinigungen
0.1 K
T
1
Supraleitfähigkeit
Supraleitende Elemente:
Al
Cd
Ga
Hg
In
Ir
La
Mo
Nb
Os
Pb
Re
T[K]
1.19
0.56
1.09
4.00
3.40
0.14
5.00
0.92
9.13
0.65
7.19
1.70
Ru
Sn
Ta
Tc
Th
Ti
Tl
U
V
Zn
Zr
T[K]
0.49
3.72
4.48
8.22
1.37
0.39
2.39
0.68
5.30
0.87
0.55
2
Isotopieverschiebung
ma  Tc  const.
Material T[K]
Zn
Cd
Sn
Hg
Pb
Tl
0.87
0.56
3.72
4.00
7.19
2.39

0.45±0.05
0.32±0.07
0.47±0.02
0.50±0.03
0.49±0.02
0.61±0.10
Material
T[K]

Ru
Os
Mo
Nb3Sn
Mo3Ir
Zr
0.49
0.65
0.92
18
0.00±0.05
0.15±0.05
0.33
0.08±0.02
0.33±0.03
0.00±0.05
0.55
3
Supraleitfähigkeit
Temperaturabhängigkeit
des kritischen
magnetischen Feldes
Im magnetischen Feld
Hc
 T2 
H c  H 0 1  2 
 Tc 
Nicht supraleitend
 

B  H  4M
Supraleiter: Meissner-Effekt



B  0  H  4M
1
 M H 
4
Supraleitend
Tc
T
Sonst:   -10-6
4
Supraleiter im magnetischen Feld
Feld außen:
Feld innen:
Magnetisierung:


Ba  H a
 

B  H a  4M  0

1 
M 
Ha
4
Ba
 
1
W   MdB  
4
0
 
Ba2
Arbeit pro
BdB  

8
Volumeneinheit
0
(Magnetisierung des Supraleiters entgegen der
Feldrichtung)
Ba
Supraleiter im magnetischen Feld liegt energetisch
höher als ohne Feld
Dies ist ein Beitrag der „supraleitenden“ Elektronen
zu der Gesamtenergie
5
Übergang „normal-supraleitend“
Thermodynamische Betrachtung
G  U  TS
B2
G U 
 TS
8
1
B2 

Tc  U  G 
S
8 
G … Gibbs-Potential (freie Enthalpie)
U … Enthalpie
T … Temperatur
S … Entropie
B … äußeres magnetisches Feld
B  8 U  G  Tc S 
T<Tc: U (und S) klein für SC, daher ist SC stabiler
T>Tc: S größer für „normal“ (geringere Ordnung), daher ist der
„normale“ Zustand stabiler
B>0 : Freie Enthalpie ist kleiner, wenn S größer ist (Normalzustand)
6
Supraleitfähigkeit
Material
T[K]
NbC
14
NbN
16
Nb3Al
18
Nb3Ge
23
Nb3Sn
18
SiV3
17
MgB2
40
YBa2Cu3O7-d
110
S.L. Bud’ko and P.C. Canfield: Temperature-dependent Hc2
anisotropy in MgB2 as inferred from measurements on
polycrystals, Phys. Rev. B 65 (2002) 212501.
7
Supraleiter
I. Art
II. Art
„Normale“ Leitfähigkeit hinter Hc
Supraleitfähigkeit verschwindet
allmählich zwischen Hc1 und Hc2
-M
-M
Supraleitend
Nicht
supraleitend
Hc
H
Hc1 Hc
Hc2 H
8
Theorie(n) der Supraleitfähigkeit
Superelektronen: keine Streuung,
die Entropie des Systems ist gleich null
(perfekte Ordnung des Systems),
große kohärente Länge
9
London Theorie (Meissner-Effekt)


Ohm: j  E
London:
Maxwell:
Meissner
Effekt:
 

c 
London: j  
A ; rot A  B
2
4L

c 
rot j  
B
2
4L
 4 
(statische Bedingungen)
rot B 
j
c
 4

Lösung:
rot rot B 
rot j
c

Bx   B0  konst

B
2
 B   2
L
B
 x 
Bx   B0 exp   
 L 
L … Londonsche Eindringstiefe
x
10
Konsequenzen der London Theorie
L beschreibt die Eindringstiefe des magnetischen Feldes in
das Material. In der Distanz L sinkt die Intensität des
magnetischen Feldes auf 1/e.
Ein äußeres Magnetfeld Ba dringt ganz homogen eine dünne
Schicht durch, wenn ihre Dicke viel kleiner als L ist. In solcher
Schicht ist der Meissner Effekt nicht vollständig.
Das induzierte Feld (im Material) ist kleiner als Ba, daher ist
das kritische, parallel zu den dünnen Schichten orientierte
Magnetfeld sehr hoch.
11
BCS Theorie der Supraleitfähigkeit
J. Bardeen, L.N. Cooper and J.R. Schrieffer, Phys. Rev. 106 (1957) 162.
J. Bardeen, L.N. Cooper and J.R. Schrieffer, Phys. Rev. 108 (1957) 1175.
1. Wechselwirkung zwischen Elektronen kann zu einem
Grundzustand der Elektronen führen, der von den aufgeregten
elektronischen Zuständen durch eine Energielücke getrennt ist.
Aber: es gibt auch Supraleiter ohne Energielücke!
E
E
12
Kohärenzlänge
Der Abstand, auf dem sich die Breite der Energielücke im räumlich
veränderlichen magnetischen Feld nicht wesentlich ändert.
London:
 
 
 
c  
j r   
Ar  ; rot Ar   Br 
2
4L
13
BCS Theorie der Supraleitfähigkeit
2. Die Energielücke entsteht aufgrund der Wechselwirkung zwischen
Elektronen über die Gitterschwingungen (Phonon). Ein Elektron
verzerrt das Kristallgitter, ein anderes Elektron „sieht“ das
verzerrte Gitter und paßt seine Energie diesem Zustand so an,
daß seine Energie sinkt. So funktioniert die Wechselwirkung
zwischen Elektronen über das Kristallgitter.
14
BCS Theorie der Supraleitfähigkeit
3. Aus der BCS Theorie folgen die Londonsche Eindringstiefe für das
Magnetfeld und die Kohärenzlänge. Damit ist der Meissner-Effekt
erklärt.
London:
 
 
 
c  
j r   
Ar  ; rot Ar   Br 
2
4L
Meissner:


B
x
 2 B  2 ; Bx   B0 exp
Kohärenzlänge:
L
0 
L
2vF
Eg
15