Preis

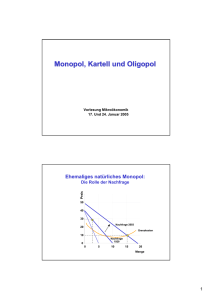
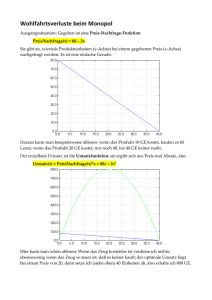
Monopol, Kartell und Oligopol
Vorlesung Mikroökonomik
17. Und 24. Januar 2005
Ehemaliges natürliches Monopol:
Preis
Die Rolle der Nachfrage
50
40
30
Nachfrage 2003
20
Grenzkosten
10
Nachfrage
1920
0
0
5
10
15
20
Menge
Preis
Wohlfahrtsmaximum im natürlichen Monopol
bei Partialbetrachtung eines Marktes
Konsumentenrente bei P = DK
50
Konsumentenrente im sozialen Optimum
40
Preis der Regulierungsbehörde
30
20
Subventionen bei P = GRK
Preis im sozialen Optimum
Durchschnittskosten
10
Nachfrage
Grenzkosten
0
0
5
10
15
20
Menge
Wohlfahrtsmaximum im
natürlichen Monopol



Die Aufspaltung eines natürlichen Monopols M in N
Teilunternehmen ist nicht sinnvoll, da Subadditivität der
Kosten: C(x)M <  C(x/N), (n = 1, ..., N)
Der soziale Planer kann verordnen P = DK, dies ist
aber für diesen Markt nur die zweitbeste Lösung
Das Optimum liegt bei P = GK, aber kein privates
Unternehmen wird (dauerhaft) mit Verlust produzieren
 Lösung 1: Subventionen in Höhe des Verlusts
 Lösung 2: Staat produziert in eigener Regie
 Problem 1: Wer trägt letztlich den Verlust
 Problem 2: dynamische Ineffizienz
Kartelle


Ausgangssituation
 mehrere (j) Anbieter
 alle sind Preisnehmer: Preiserhöhung eines
Einzelnen führt zum Ausscheiden aus dem Markt
Anreiz: Gewinnmaximierung
 Strategie: koordinierte Preispolitik
 Umsetzung: gemeinsames Auftreten als
Angebotsmonopol (wie grosse Firma mit j
Betriebsstätten)
 gewinnmaximierender Preis ist durch den
Cournotschen Punkt fixiert
– Menge geht zurück
– Preis steigt
– Gesamtwohlfahrt nimmt ab
– Konsumentenrente sinkt
– aggregierter Gewinn steigt
Aber: Kartelle sind instabil:
Feste Aufteilung der Menge
xC auf j Firmen gibt Anreiz zu
„opprtunistischem“ Verhalten
Preis
Graphische Analyse des Kartells
Cournot-Punkt
50
Grenzkosten
40
30
20
Marktgleichgewicht
10
Nachfrage
Grenzertrag
0
0
5
10
15
20
In der realen Wirtschaft befinden sich die Märkte
zwischen den Extremen vollständige Konkurrenz
und Monopol.


Die Unternehmen konkurrieren über:

Entwicklung neuer Produkte und Differenzierung der
bestehenden (Automodelle)

Entwicklung verschiedener Produktionstechniken
Viele Unternehmen verfügen über eine gewisse Marktmacht:


Wenn sie den Preis erhöhen, verlieren sie nur einen Teil der
Kunden.
Viele Märke sind über Zulassungsbewilligungen (Ärzte),
Subventionen (Landwirte), Zölle usw. reguliert
Oligopol

Einige wenige Anbieter verkaufen das gleiche Produkt.

Die Interdependenz zwischen Aktionen der einzelnen
Anbietern ist von zentraler Bedeutung.


Wie reagieren die Konkurrenten auf eine
Preissenkung?

Wie reagieren sie auf eine Werbekampagne?
Jeder Anbieter muss bei seinen Entscheidungen
die Reaktionen der anderen Anbieter voraussehen.
Preis im Oligopol

Höchster Gewinn, wenn sich die Unternehmen
gemeinsam wie ein Monopol verhalten, d.h. ein
Kartell bilden.
 Dilemma: Kurzfristig lohnt es sich, zu einem
niedrigeren Preis anzubieten als die anderen
Unternehmen, d.h. Kartelle sind instabil.
Beispiel Oligopol: Wasserangebot


A
2 Anbieter (A und B)
 Grenzkosten = 0
 Fixkosten = 0
maximaler Gewinn:
Preis
Menge
Gewinn
60
30
1‘800
gewinnmax. Angebot im Oligopol
=
gewinnmax. Angebot im Monopol
Preis
120
100
80
B
60
30
1‘800
60
40
20
Nachfrage
Grenzertrag
0
0
20
40
60
80
100
Liter Wasser / Woche
120
Beispiel Oligopol: Wasserangebot


A
2 Anbieter (A und B)
 Grenzkosten = 0
 Fixkosten = 0
maximaler Gewinn:
Preis
120
Preis
Menge
Gewinn
60
30
1‘800
wenn A Preis
senkt und B nicht
100
80
B
60
30
1‘800
60

Wenn A Preis senkt:
Preis
Menge
40
Gewinn
A
50
70
3‘500
B
60
0
0
20
Nachfrage
Grenzertrag
0
0
20
40
60
80
100
Liter Wasser / Woche
120
Beispiel Oligopol: Wasserangebot


A
2 Anbieter (A und B)
 Grenzkosten = 0
 Fixkosten = 0
maximaler Gewinn:
Wenn sich A und B
gegenseitig unterbieten
sinkt der Preis auf 0
=
Preis im vollkommenen
Wettbewerb
Preis
120
Preis
Menge
Gewinn
60
30
1‘800
100
80
B
60
30
1‘800
60

Wenn A Preis senkt:
Preis
Menge
40
Gewinn
A
50
70
3‘500
B
60
0
0
20
Nachfrage
Grenzertrag
0
0
20
40
60
80
100
Liter Wasser / Woche
120
Beispiel Oligopol: Wasserangebot


A
2 Anbieter (A und B)
 Grenzkosten = 0
 Fixkosten = 0
maximaler Gewinn:
Preis
Menge
Gewinn
60
30
1‘800
Preis
120
100
80
B
60
30
1‘800
60

Wenn A Menge erhöht:
Preis
Menge
40
Gewinn
A
40
50
2‘000
B
40
30
1‘200
20
Nachfrage
Grenzertrag
0
0
20
40
60
80
100
Liter Wasser / Woche
120
Nash-Gleichgewicht

Nash-Gleichgewicht: Situation, in der niemand sein Verhalten
verändern wird, solange der andere sein Verhalten nicht verändert.
Preis
Lohnt es sich für A die
Menge auf 60 zu erhöhen,
wenn er sicher ist, dass B
weiterhin 30 anbietet?
120
A
Preis
Menge
Gewinn
60
30
1‘800
100
80
B
60
30
1‘800
60

Wenn A Menge erhöht:
Preis
Menge
40
Gewinn
A
40
50
2‘000
B
40
30
1‘200
20
Nachfrage
Grenzertrag
0
0
20
40
60
80
100
Liter Wasser / Woche
120
Aggregiertes Angebot im Oligopol

Wenn die Anbieter im Oligopol die Mengenentscheidungen
zur Gewinnmaximierung wählen:
 Angebot grösser als im Monopol und kleiner als im
vollkommenen Wettbewerb
 Marktpreis kleiner als im Monopol und grösser als im
vollkommenen Wettbewerb
Spieltheorie und Oligopol




Spieltheorie: Analyse von Verhalten in
strategischen Situationen.
Analysiert Situationen, in denen das Ergebnis
davon abhängt, wie sich die anderen verhalten
Ich überlege mir wie:
 Wie werden sich die anderen verhalten?
 Wie werden die anderen auf meine Aktionen
reagieren?
Das Gefangendilemma zeigt den Konflikt zwischen
Kooperation und individualistischem Verhalten.
Gefangenendilemma:
Die Tat gestehen oder nicht oder nicht?
Soll ich gestehen?
meine Strafe
NEIN
Strafe für meinen
Komplizen
nach 2 Tagen frei
NEIN
Wird mein
Komplize
gestehen?
JA
nach 2 Tagen frei
3 Monate
Gefängnis
sofort frei
dominante
Strategie
JA
dominante
Strategie
sofort frei
3 Monate
Gefängnis
2 Monate
Gefängnis
2 Monate
Gefängnis
Gefangendilemma



Dominante Strategie: Unabhängig von dem was
mein Komplize macht, ist es für mich am besten,
wenn ich gestehe.
So werden wir beide gestehen.
 Das Ergebnis ist nicht paretooptimal.
 Wenn wir beide nicht gestehen würden, hätten wir
beide einen höheren Nutzen.
Oft ist ein Gefangenendilemma Ursache für ein
Marktversagen.
Beispiel
Rüstungswettlauf im kalten Krieg:
Aufrüsten und Atomkriegsrisiko
USA
aufrüsten
UdSSR
abrüsten
aufrüsten
abrüsten
hohes Risiko
hohes Risiko
schwach
stark
stark
schwach
geringes Risiko
geringes Risiko
Beispiel OPEC:
Produktion erhöhen oder nicht


Niedrige Produktion wäre
die beste Lösung für beide.
Aber „Produktion erhöhen“
ist die dominante Strategie.
Ergebnis = Gewinn
Saudi-Arabien
hoch
niedrig
hoch
40
40
30
60
niedrig
60
30
50
50
Iran
Beispiel Oligopol:
Lebensmitteldetailhandel nach Umsätzen 2001
andere
17%
Primo/visavis
5%
Migros
39%
Denner
5%
Coop
34%
Migros + Coop = 73%
Quelle: Schweiz. Marketing Forum - Detailhandel Schweiz 2002/03
Preise senken - JA oder NEIN
Wenn beide die Preise senken,
machen beide keinen Gewinn!
Migros
NEIN
JA
NEIN
100
100
140
- 40
JA
- 40
140
0
0
COOP
Preise senken - JA oder NEIN
Ein Verzicht auf Preiswettbewerb
wäre die beste Lösung für beide
Migros
NEIN
JA
NEIN
100
100
150
- 50
JA
- 50
150
0
0
Es lohnt sich ein
Preiskartell zu bilden
COOP
Welche Situation ist
für die Gesellschaft
paretooptimal?
Das Oligopol: formale Lösung (I)
1. Marktangebot: X = x1 + x2 + x3 + . . . + xn
Hier: Spezialfall “Duopol”: X = x1 + x2
2. Marktpreis: p(X) = p(x1 + x2 + x3 + . . . + xn)
3. Erlös des einzelnen Unternehmens i im Duopol:
Ei(xi) = xi . p(X)
Für p(X) = a - bX (lineare Preisabsatzfunktion) ergibt sich
E1 = (a - bX) x1 = (a - bx1 - bx2) x1 = ax1 - bx12 - bx1x2
Der Grenzerlös für Firma 1 im Duopol ist
GE1 = a - 2bx1 - bx2 = a - b (2x1 + x2) = a - b(X + x1)
Das Oligopol: formale Lösung (II)
Gewinnfunktion eines Unternehmens i in Abhängigkeit von xi lautet:
G(xi) = E(xi) - C(xi)
Notwendige Bedingung für Gewinnmaximum ist:
G‘(xi) = 0  C‘(xi) = E‘(xi)
Im Falle des Duopolisten 1 heisst dies (bei linearer Nachfragefunktion):
C‘(x1) = a - 2bx1 - bx2
Auflösen der Optimalitätsbedingung nach x1 ergibt
die Reaktionsfunktion R1(x2) des Duopolisten 1:
R1(x2) = x1= [a - bx2 - C‘(x1)] / 2b = [a - C‘(x1)] / 2b - x2/2
Entsprechend gilt für den Duopolisten 2:
R2(x1) = x2= [a - bx1 - C‘(x2)] / 2b = [a - C‘(x2)] / 2b - x1/2
Das Oligopol: formale Lösung (III)
Vereinfachende Annahme: identische und konstante Grenzkosten
in beiden Firmen:
K‘(x1) = K‘(x2) = k
Die Reaktionsfunktionen vereinfachen sich damit zu:
R1(x2) = x1= (a - bx2 - k) / 2b = (a - k) / 2b - x2/2
R2(x1) = x2= (a - bx1 - k) / 2b = (a - k) / 2b - x1/2
Duopol bei identischen und konstanten
Grenzkosten
x1= (a - k) / 2b - x2/2
x2= 0  x1=(a-k)/2b
x1= 0  x2=(a-k)/b
x2
(a-k)/b
x2= (a - k) / 2b - x1/2
x1= 0  x2=(a-k)/2b
x2= 0  x1=(a-k)/b
R1(x2
)
(a-k)/2b
R2(x1)
(a-k)/2b
(a-k)/b
x1
Simultanes Gleichgewicht
Durch gegenseitiges Einsetzen der Optimalitätsbedingungen ergibt
sich die optimale Menge für Firma 1
a  b  R 2  x1   GK1
x1 
2b
 a  bx1  GK 2 
a  b 
  GK1
2b



2b
a  2 GK1  GK 2

3b
Rechenweg: Ausmultiplizieren und x1-Terme zusammenfassen.
Für Firma 2 gilt Entsprechendes.
Simultanes Gleichgewicht bei
identischen und konstanten
Grenzkosten
Hier wieder die vereinfachende Annahme identischer und konstanter
Grenzkosten in beiden Firmen: K‘(x1) = K‘(x2) = k
Im simultanen Gleichgewicht gilt:
x1= (a - bx2 - k) / 2b = (a - k) / 2b - x2/2
x1 = (a - k) / 3b
x2 = (a - k) / 3b
Gesamtangebot:
X = x1 + x2 = (a - k) / 3b + (a - k) / 3b = 2(a - k)/3b
Duopol: nichtkooperatives Gleichgewicht
x2
(a-k)/b
Cournot-Duopolpunkt
R1(x2
)
(a-k)/2b
(a-k)/3b
R2(x1)
(a-k)/3b
(a-k)/2b
(a-k)/b
x1
Duopol: andere Gleichgewichte
x2
Beachte: E‘(X) = a - 2bX
GK = E‘(X)  k = a - 2bX
 X = (a-k)/2b = (1/2)(a-k)/b
Beachte: P = a - bX
P = GK  k = a - bX
 X = (a-k)/b
Cournot-Duopolpunkt:
Xc = (2/3)(a-k)/b
(a-k)/b
Stackelberg-Gleichgewicht:
Xs > Xc
(a-k)/2b
(a-k)/3b
Kollusionslösung:
Xk = (1/2)(a-k)/b < Xc
Konkurrenzlösung:
X* = (a-k)/b > Xs
(a-k)/3b
(a-k)/2b
(a-k)/b
x1
Aufgabe: Wohlfahrtsverlust durch
Monopole / Kartelle
MONOPOL
inverse Nachfragefunktion:
P(x) = -2x + 12
Grenzkostenkurve:
GRK(x) = 2x
Berechnen Sie den Wohlfahrtsverlust gegenüber
dem Marktergebnis bei vollständiger Konkurrenz
(Hinweis: grafisch oder rechnen Sie aus)!