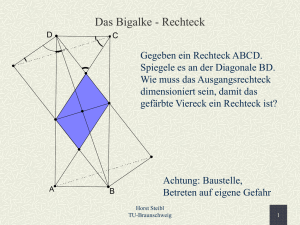
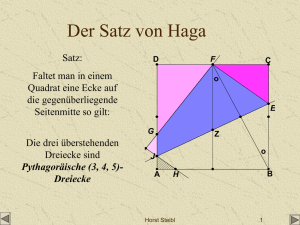
Die goldenen Linien auf dem Geobrett und das ägyptische Dreieck

Horst Steibl, TU Braunschweig
GDM-Tagung Berlin 2007
Die goldenen Linien auf dem
Geobrett und das ägyptische Dreieck
Wie Tim und Tom, die Winkelwichtel, helfen,
den Durchblick zu behalten
Horst Steibl
1
C
Die Aufgabe:
P
Q
M
A
L
B
Falten Sie in einem quadratischen Blättchen die gezeichneten
Linien exakt durch Punkt-auf-Punkt-Faltung und beweisen Sie,
dass die gefärbten Dreiecke ägyptische Dreiecke sind.
Erlaubte Hilfsmittel: Winkelsumme im Dreieck, Strahlensätze,
Ähnlichkeit,
Horst Steibl
2
Die Diagonale im Doppelquadrat
Halbiere das Quadrat längs einer
Mittellinie. Du erhältst zwei
Rechtecke, deren lange Seiten
doppelt so lang sind wie die kurzen.
Man bezeichnet es auch als
S
Doppelquadrat.
B
P
M
In Jedem Rechteck gilt:
Um die Diagonale zu falten, faltet man zunächst die
Mittelsenkrechte der Diagonale. Bringt man dann
die Endpunkte dieser Faltlinie aufeinander, so erhält
man die Diagonale.
Die diagonale Raute im Rechteck
Horst Steibl
3
Die goldenen Linien im Quadrat
5/4
1²
(1/2)²
Dies Verbindungslinie eine Seitenmitte des
Quadrates mit einem nicht benachbarten Eckpunkt
bezeichne ich als goldene Linie im Quadrat.
Berechnet man die Länge dieser Strecke im
Einheitsquadrat , so ergibt sich: g = ½*5
t = ½ + ½*5 = 1,618...
Somit lässt sich hiermit die Konstante t des
goldenen Schnittes konstruieren
Horst Steibl
4
Das 3. Elementardreieck
Dieses Dreieck, dessen Katheten im Verhältnis
1 : 2 stehen heißt auch nach Platon:
Elementardreieck Nr 3
Man kann sie zum Quadrat mit Loch umlegen
und damit etwa ausgehen vom 10 * 10 Quadrat
die Länge von g elementar berechnen ~:
A = (1 + ¼)
Beim Versuch, solche Quadrate mit Loch zu
legen (es gibt noch eine 2. Möglichkeit),
kann sich folgendes ergeben:
Horst Steibl
5
Das goldene Rechteck
Es entsteht ein Rechteck mit Loch,
dessen Seiten im Verhältnis des
goldenen Schnittes stehen. Für das
Loch gilt das gleiche.
Hans Walser´s
goldene Spirale
,6 cm
,2 cm
2,3 cm
Horst Steibl
6
Figuren aus vier Dreiecken
Grundfiguren:
Quadrat, Rechteck.
Raute, Trapez
Parallelogramm
Spiegelachsen
Figuren mit Loch
Drehsymmetrie
Horst Steibl
7
Die Knautsche Figur
Wie viele goldene
Linien sind das?
Zeichnet (oder faltet) man alle 8 goldenen Linien im
Quadrat, so entsteht eine ansprechende Sternfigur: die
Knaut´sche Figur
Horst Steibl
8
Die Knaut´sche Figur auf dem Geobrett
Horst Steibl
9
Das Parallelogramm und der Drachen als
erzeugende Elemente der Knaut´schen Figur
Horst Steibl
10
Vierecke aus den goldenen Linien
1/5
1/3
1/4
½ - 1/12 –3/20= 4/15
1 – 3* 1/8 – 2* 4/20 = 9/40
½ - 1/12 –1/8 = 7/24
Horst Steibl
11
17
1717
16
1616
15
1515
14
1414
13
1313
12
1212
11
1111
10
1010
9
99
8
88
7
77
Schnittpunkte
Der
Drittelpunkt
Verhältnis
6
6 In 6welchem
sich diese
55
5 schneiden
Linien hier ?
44
4 goldenen
3
33
2
22
1
1
Es gibt drei
Klassen von
Schnittpunkten
Diagonalen
des Rechtecks
2
Die Diagonalen im Trapez teilen einander
im Verhältnis der parallelen Seiten
Das Verhältnis heißt hier 1 : 2
Damit können wir
1 1 das Blatt in 9
Der Punkt drittelt jede Querlinie , die von
Quadrate
1416
einer
Seite
zur
Gegenseite
geht
4 4 65 5 76 6 8 7 7 98 8 10
9 9 11
101012
111113121214
131315
14
151517
161618171719
1818
191921
202022212123
222224
232325
242426
25252
21 1 3 2 2 43 3 5zerlegen
20
-1-1 1
-1-1
-1
-2
-2-2
Horst Steibl
12
g1 und g2 schneiden
im rechten
Winkel
Dersich
Fünftel-Punkt
2
1
4
10
3
2
1
5
Im rechtwinkligen Dreieck teilt die Höhe
auf die Hypotenuse dieses in zwei zum
Ausgangsdreieck ähnliche Dreiecke
Sie teilt diese im Verhältnis der Quadrate
der Katheten
2
5
4
3
Damit haben wir gezeigt, dass diese 3 g-Linien
ein ägyptisches Dreieck bestimmen. Später dazu
mehr. 10
5
Falten Sie ein 5 + 5 Feld ohne aufzurollen!
Nicht durch den Punkt, sondern auf den Punkt falten
Horst Steibl
13
Die Höhe im rechtwinkligen Dreieck
Der Höhensatz lautet:
h² = p * q
q² + h² = a²;
p² + h² = a²
q² + p*q = a²
P² + p*q = b²
q(q + p) = a²
p(p + q) = b²
q : p = a² : b²
Horst Steibl
14
Das 25-er Feld
2
4
Der Schnittpunkt bestimmt lotrecht einen 2-erStreifen und einen 3-er-Streifen.
Halbiere zuerst den 2-er-Streifen
2´
4
3´
Nun hast du ein Feld, das 4 Streifen breit ist.
Halbiere dieses. Du bekommst zwei 2-er-Streifen.
Halbiere zunächst den äußeren. Als letztes
knickst du die Linie durch den Teilungspunkt (4er-Streifen halbieren)!
Quer: Halbiere die Viererstreifen; dann den unteren 2-er-Streifen. Falte von oben
auf die unteren Knick(4=2 +2). Halbiere den untere 2.er-Streifen. Die letzte Faltlinie
geht wieder durch den Teilungspunkt.
Horst Steibl
15
Bruchteile
2 2
5
10
1/
2´
6
2´
* ½= 1/12
3´ 3´
1/
1/
*
½=
10
20
Horst Steibl
1/
1/ = 1/
*
3
4
12
16
7
7
6
Die ägyptischen
Dreiecke 6
5
5
Lage4 im Punktgitter?
9 -15
-8 -14
-7 -13
-6 -12-5 -11-4 -10-3 -9-2 -8-1 -7
4
3
3
2
2
1
1
-6 1 -5 2 -4 3 -3 4 -2 5 -1 6
-1
7 1 8 2 9 3 10 4 11 5 12
-1
-2
-2
Woran erkennt man sie?
3:4:5
4
5
6
7
8
9
10
R; 3 : 4
11
12
13
14
15
-3
16
17
-4
R und einen zweiten
ägyptischen Winkel!!
R; 4 : 5
18
19
20
21
24
25
27
28
29
30
31
= 36,869...°-5
sehr krumm
-7
Horst Steibl
-8
23
x
arctan(4/3) = 53,130...°
-4
-5 arctan(3/ )
4
-6
22
-3
26
-6
-7
-8
17
32
Tim und Tom in ihren Kammern
tan (Tom) = ½
5, 11, 14 - Kammer
Tom: Der spitzere Winkel im diagonal halbierten
5, 10, 11 - Doppelquadrat
Kammer
Tim + Tom = ½ R
Horst Steibl
18
Die Doppelkammern
m
Tim hat einen Zwillingsbruder, Timm mit
zwei m. Wenn der zu Besuch kommt,
schlafen sie in der Tim-Timm Ecke.
Der Zwillingsbruder von Tom
kommt auch ab und zu. Jetzt
kann man gut sehen,dass sie
Das ist also die Tom-Tom-Ecke
etwas breitere Hüte haben als
Horst Steibl
19
die Tims.
Zerlege und du findest das Zauberwort
N
K
I
A
P
T
R
S
U
A
Horst Steibl
oiio
P
oi
A
iooi
N
o
K
ES
ii
R
oiiooi
A
oo
T
oiioo
I
iio
U
ooi
20
S
y 14
13
Die Winkel des ägyptischen Dreiecks
12
11
y 12
11
10
10
oo
y 12
11
10
9
oo
9
8
8
7
7
6
ii
6
5
5
9
8
7
6
ii
5
4
y 12
4
4
Das (7,11,11)-D
3
2
3
11
2
o
o
1
2
Genau
dann
ist ein
i 10
i
1
6
7
8 1 9 10
13 14 15
Dreieck
x 11 12 ein
i 9-1 -1 1i 2 3 4 5rechtwinliges
x
-20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10 -9 -8 o-7 -6
-5 -4 -3 -2 pythagoräisches
-1
1
2
3
o
3,4,5
–
-20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10 -9 8-8 -7
-6 -5 -4 -3 -2 -1-1
1
2
3
-2
o i
Dreieck, wenn
es einen oo-1
7
i
-3
-2
Winkel
oder
-2 einen ii-winkel
6
-4
o
hat.
Das (10,11,11-D)
5
3
-5
4Horst -6
Steibl
3
-7
21
Lösung unserer Aufgabe
Augenscheinlich!
Zwei lotrecht aufeinander stehende Geradenpaare schneiden sich
unter gleichen Winkeln
Horst Steibl
22
-2
9
8
7
Trigonometrischer Einschub
6
5
a = arc tan (4/3)
4
oo
3
4
2
1
2
a= oo
-1
1
-1
3
2
3
o = arc tan (1/2)
4
5
6
7
8
9
10
11
12
a13=142 15* o16
x
1
-2
-3
-4
arc tan 4/3 = 2* arc tan 1/2
-21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10
-9
-8
-7
-6
-5
-4
-5
-6
Horst Steibl
23
-3
-2
Das pythagoräische Dreieck aus dem Doppelquadrat
Nach einem Vorschlag von Hans Walser
Hier ist in einem Doppelquadrat,
also einem Rechteck mit den
Seitenverhältnissen 1 : 2
o
o ii
eine Ecke auf die Gegenecke
gefaltet. Damit haben wir die
Mittelsenkrechte der Diagonale
gefaltet.
o
Betrachten wir den
Rechteckwinkel unten links:
Also muss des blaue Dreieck
ein ägyptisches Dreieck sein
Für den Dreieckswinkel bleibt
ein Tim-Tim-Winkel übrig!
Horst Steibl
24
Der Satz von Haga
oo
Faltet man in einem Quadrat eine
Ecke auf eine gegenüberliegende
Seitenmitte, so sind die drei
überstehenden Dreiecke
pythagoräische (3,4,5)-Dreiecke
ii
ii
Falte die Mittelsenkrechte der
Diagonale des rechten Doppelquadrates und die Diagonale
ii
ii
Horst Steibl
25
Pyth aus dem Doppelquadrat
2:1=1:½
a´
c´
4:2=2:1
b´
Vertauschen der
Funktion:
Diagonale
Mittelsenkrechte
a= ½ (4 – 1) = 1 ½
8:4=4:2
a´ = ½ (8 – 2) = 3
b´= 4
c´ = a´+ 2 = 5
Horst Steibl
26
Maße des Rechtecks?
Faltet man in einem Rechteck mit
Seitenverhältnis u : v
(u > v) die
Diagonale und ihre Mittelsenkrechte (in
umgekehrter Reihenfolge) und vertauscht
ihre Funktion, so kommt man zu einem
ähnlichen Rechteck.
Es handelt sich um ein Drehstreckung
a = 90° und p = v/u.
Wie kann ich die Maße des Rechteckes aus den gegebenem Verhältnis berechnen? Geht
das auch bei anderen Rechtecken? Ergeben sich da auch pythagoräische Dreiecke?
Die Seiten des entsprechenden Dreiecks stehen bei ganzzahligem Verhältnis
der Rechteckseiten dann immer im Verhältnis eines pytagoräischen
Zahlentripels.
Horst Steibl
27
Das indische Dreieck 3 : 2
Tauschen der Funktion:
Diagonale - Mittelsenkrechte
3:2=2:x
x = 4/ 3
3 : 2 = 2 : 4/ 3
9/6=6/4
a=5
b = 12
c = 5 + 8 = 13
(9 – 4)/2 = 5/2
y = 5 /2
25 + 144 = 169
18 : 12 = 12 : 8
x ´= 8
y´ = 5
x´+y´= 13
y
x
x+y
Horst Steibl
Ist u : v das ganzzahlige Verhältnis
der Rechteckseiten, u > v
und u – v ungerade, so erweitere
man die Verhältnisse der Rechtecke
mit 2u.
Auf diese Weise erhält man die
Maße des gesuchten Rechteckes.
28
Rechteck 7 : 4
65
32
„erweitere“ mit
2*u=2*7
7 : 4 = (7 * 2*7) : (4 * 2*7) = 98 : 56
Rechtecksmaße
56 * (4 /7) = 32
kurze S. kl. Re.
(98 – 32) /2 = 33
Kathete
32 + 33 = 65
Hypotenuse
56
33² + 56² = 65²
1089 + 3136 = 4225
33
98
Sind u und v die Parameter des Seitenverhältnis mit u > v
und u, v gekürzt und u – v nicht gerade so gilt
a : b : c = (u² - v²) : 2u : (u² - v²)
Horst Steibl
29
Berechnung der Zahlentripel: Verhältnis u : v
Die kurze Seite x des drehgestreckten Rechtecks berechnet sich zu
x = v * v / u = v²/u
Damit ergibt sich für den Abschnitt y
y = 1/2 ( u - x) = 1/2 ( u - v²/u)
x
y
z
v
Setzen wir die Seiten y, v und z des
pythagoräischen Dreiecks ins Verhältnis:
y : v : z = 1/2 ( u - v²/u) : v : (v²/u) + 1/2 ( u - v²/u)
"erweitern" wir diese Terme mit 2u so ergibt sich
u
y : v : z = (u² - v²)
Horst Steibl
: (2*u*v ) :
(u² + v²)
30
Hans Walser
http://www.math.unibas.ch/~walser/Miniaturen
Hans Walser, (20060812) Trigonometrie im Schachbrett,
Hans Walser, pythagoräische Dreiecke, 8th International Conferenc on
Geometrie Part 2´
Hans Walser, (20060408b) Falten von Rechtecken
Alfred Hoehn, Der wiedergefundene Schatz
Horst Steibl, Das Geobrett im Unterricht, Franzbecker, 2006
Horst Steibl, Geometrie aus dem Zettelkasten, Franzbecker, 1999
http://www.alfredhoehn.ch/wiedergefundene%20Schatz.pdf
http://www.madin.tu-bs.de/homepage/steibl/Startseite.html
http/Miniaturen/
Horst Steibl
31
Rechtecke mit irrationalen Seitenverhältnissen
1
3
/4
2
1
/4
1
/2
2
2
Horst Steibl
32
Vielen Dank für Ihre Aufmerksamkeit
Horst Steibl
33
yyy 18
18
18
18
17
17
17
17
16
16
16
16
180°:
15
15
15
15
Ein Achteck?
14
14
14
14
o
13
13
13
13
ii
12
12
12
12
11
11
11
11
oo
126,8699
126,8699
126,8699
126,8699°°°°°
126,8699
10
10
10
10
9999
ii
126,8699
126,8699
126,8699
126,8699°°°°°
126,8699
8888
o
7777
cm
333
3 cm
cm
cm
3 cm
143,1301
143,1301
143,1301 °°°°
143,1301
143,1301 °
cm
333
3 cm
cm
cm
6666
5555
143,1301 °
143,1301
143,1301
143,1301 °°°°
143,1301
3 cm
4444
3333
2222
1111
-4
-4
-4
-4
-3
-2
-3
-3 -2
-2
-3
-2
-1
-1
-1
-1
11111
-1
-1
-1
-1
-2
22222
33333
4444
4
5555
5
6666
6
77777
8888
8
9999
9
Horst Steibl
10
11
12
13
14
15
16
17
18
19
20
21
10
11
12
13
14
15
16
17
18
19
20
21
10
10 11
11 12
12 13
13 14
14 15
15 16
16 17
17 18
18 19
19 20
20 21
10
11
12
13
14
15
16
17
18
19
20
21
34
s. Hans Walser
Dreiecksmetamorphosen
Horst Steibl
35