Inner-sphere oder outer

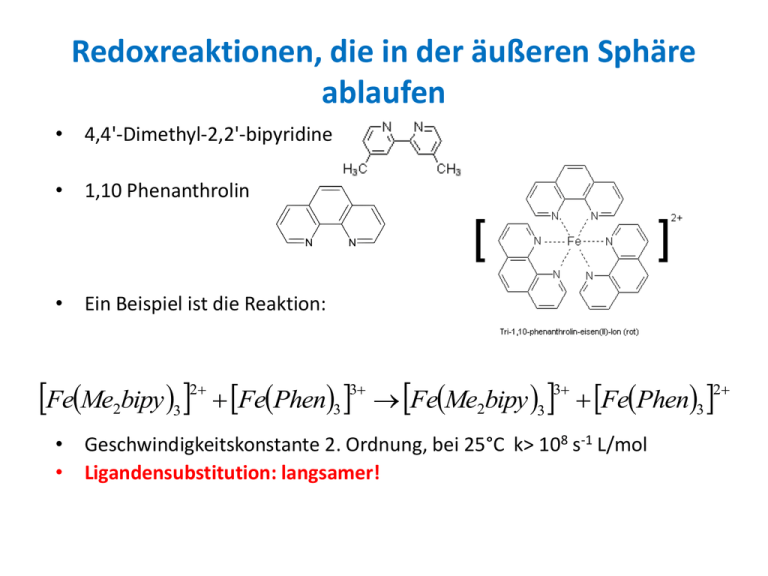
Redoxreaktionen, die in der äußeren Sphäre
ablaufen
• 4,4'-Dimethyl-2,2'-bipyridine
• 1,10 Phenanthrolin
• Ein Beispiel ist die Reaktion:
FeMe bipy  
2
2
3
 FePhen3   FeMe2bipy 3   FePhen3 
3
3
• Geschwindigkeitskonstante 2. Ordnung, bei 25°C k> 108 s-1 L/mol
• Ligandensubstitution: langsamer!
2
• Der eindeutige Beweis, dass eine Redoxreaktion unter
Erhalt der Koordinationsschalen verläuft, ist schwierig d.h.
• macht eine Kombination von Reaktanden notwendig, bei
denen die Redoxreaktion wesentlich rascher verläuft als
irgend ein Substitutionsprozess am Oxidations- oder
Reduktionsmittel.
• Am einfachsten zu behandeln ist der Fall, in dem keine
chemische Veränderung erfolgt,
• z.B. Reaktion zwischen zwei Komplexen mit gleichem
Zentralatom und gleicher Koordinationshülle aber
verschiedener Oxidationsstufe (=Austauschreaktion)

54
25
 

Mn O4 
VII
55
25
VI
Mn O4

2


54
25
VI
Mn O4
 
2
55
25
Mn O4
Natürliches Mangan besteht zu 100% aus dem Isotop Mn-55.
Markiert werden kann mit dem radioaktiven Isotop Mn-54
(Elektroneneinfang, t1/2 = 303 d)
Bei solchen Reaktionen hat die e- Übertragung keine Konzentrationsänderung
irgendeines der Reaktanden zur Folge!
Daher gilt
VII
G  0
0
Methode zur Bestimmung der Reaktionsgeschwindigkeitskonstante:
Mischung von Kaliumpermanganat (violett, diamagnetisch) mit
Kaliummanganat (grün, paramagnetisch) in wässr. Lsg. mit radioaktiv
markiertem KMnO4 versetzt, in regelm. Zeitabständen Proben entnommen,
Manganat als BaMnO4 gefällt, Verteilung der Radioaktivität als Funktion der
Reaktionszeit gemessen. Auswertung nach der McKay Gleichung.


• McKay Gleichung:
ln( 1  F )   k  ( A  B )  t

AX   AX 
F
AX   AX 


0


e
0
•
Falls sich optisch stabile Enantiomere eines Komplexes herstellen lassen, kann
man die optische Drehung messen:
  Os bipy 3     Os bipy 3     Os bipy 3     Os bipy 3 
2
•
3
3
Die Elektronenübertragung hat eine Änderung der resultierenden optischen
Drehung zur Folge
0
G  0
•
Falls gleiche Konzentrationen an Reaktanden eingesetzt werden, ist die
Geschwindigkeit der Racemisierung ein Maß für die Geschwindigkeit der
Elektronenübertragung.
•
Bipy= 2,2‘ Bipyridin
2
Franck-Condon-Prinzip
• Der Elektronenübergang erfolgt innerhalb einer Zeitspanne (10-15 s)
• die wesentlich kürzer ist als die Zeit, die ein Kern benötigt, um seine
Stellung zu ändern (>10-13 s)
• Der elektronische Übergang ist sehr schnell im Verhältnis zur
Schwingungsbewegung der Kerne. Dies bedeutet, dass die Atome
während des e- Überganges an ihren Plätzen verharren.
• Da das Elektron eine statische Situation vorfindet, kann während des
Elektronenüberganges keine Zufuhr oder Abfuhr von Rotations- oder
Schwingungsenergie erfolgen, auch keine Änderung der räumlichen
Anordnung der Atome.
• Ein Elektronenübergang ist nur dann erlaubt, wenn er keinen
Energieeffekt und keine Änderung der Geometrie des
Übergangszustandes erfordert!
FeH O 
2
2
6
 FeH 2O6   FeH 2O6   FeH 2O6 
3
3
2
3
2
• FeH 2O6  und FeH 2O6  haben verschiedene Geometrie d.h. die
Gleichgewichts-Bindungslänge zw. Zentralatom und Liganden ist
verschieden.
• Im Grundzustand ist daher kein e- Übergang möglich. Beide
Reaktionspartner, Fe(II) und Fe(III) müssen in angeregten
Schwingungszuständen vorliegen.
1 Å= 0.1 nm
Outer-sphere Redoxreaktionen, Zusammenfassung
• Es gilt das Franck-Condon Prinzip: Nur wenn die MetallLigand Bindungen vor der Reaktion zusammengepresst
bzw. gedehnt werden, sodass die Geometrie des ÜZ sich
während des Elektronenüberganges nicht ändert, kann
der e- Übergang auch wirklich stattfinden.
• Diese Anregungsenergien sind Beiträge zur
Aktivierungsenthalpie H  der Reaktion.
• Ein zweiter Faktor, der zur Aktivierungsenthalpie
beiträgt, ist die Neuanordnung von äußeren LMMolekülen.
• Elektrostatische Wechselwirkungen zwischen den
Reaktanden spielen dagegen bei outer-sphere
Redoxreaktionen keine besondere Rolle! Viele
Reaktionen zwischen hochgeladenen Ionen gleichen
Ladungsvorzeichens sind sehr rasch.
RuCl63-
Aktivierungsentropien bei outer-sphere
Redoxreaktionen
• Vor allem durch Solvatationseffekte bestimmt
• Negative Aktivierungsentropien sind für Reaktionen zwischen
Ionen desselben Ladungsvorzeichens zu erwarten (ÜZ stärker
solvatisiert).
• Mit steigender Gesamtladung des ÜZ wird S  immer
negativer.
• Elektronentransferreaktionen, bei denen eine chemische
Änderung erfolgt, sind gewöhnlich viel schneller als die
entsprechenden Austauschreaktionen.
•
z.B. ist die Cr2+ - Fe3+ Reaktion viel schneller als die Cr2+ - Cr3+
und die Fe2+ - Fe3+ Reaktion.
•
Es besteht ein Zusammenhang zwischen dem ΔG0 der
Redoxreaktion und der Reaktionsgeschwindigkeit!
• Für eine Reihe verwandter Reaktionen gilt: je negativer das
ΔG0 desto niedriger das G  , desto größer die
Reaktionsgeschwindigkeitskonstante. (Eine thermodynamisch
begünstigte Reaktion ist also auch kinetisch begünstigt!)
• Die Geschwindigkeitskonstanten von outer-sphere
Redoxreaktionen lassen sich nach der Marcus-Theorie
theoretisch berechnen.
Rudolph Arthur Marcus
• Rudolph A. Marcus wurde für seine wichtigen Beiträge zur Theorie des
outer-sphere Elektronentransfers in chemischen Systemen 1992 mit dem
Nobelpreis geehrt.
• In biologischen Stoffwechselprozessen wie zum Beispiel der
Primärreaktion der Photosynthese spielt der outer-sphere
Elektronentransfer die zentrale Rolle.
Nobelpreis für Chemie 1992
Rudolph A. Marcus (USA, *1923)
Theorien zur Elektronenübertragung
http://www.cce.caltech.edu/faculty/marcus/
•
Die Marcus-Gleichung ist fast immer sehr gut
erfüllt.
•
Ein großer Unterschied zwischen den
berechneten und den experimentell
bestimmten Geschwindigkeitskonstanten weist
darauf hin, dass ein anderer Mechanismus
(inner-sphere) vorliegt.
•
Die Marcus-Gleichung lässt sich gut verstehen,
wenn man näherungsweise annimmt, dass die
Reaktionspartner im Fall der outer-sphere
Redoxreaktion keinen gemeinsamen aktivierten
Komplex bilden, sondern getrennt voneinander
aktiviert werden.
     
Gl.5 & Gl.2:

G AB
 G A   G B   G A   GB 
Gl.6 & Gl.1:

0
GAB
 G A  G B   GAB
 G A  G B 
   
Gl.6
 
Gl.7
Gl.7&Gl.3&Gl.4:
   
 

0


GAB
 GAB
 GAA
 G A  G A  GBB
 G B   G B 
Gl.8&Gl.2:

0


2 GAB
 GAB
 GAA
 GBB
G

AB

1
0


  GAB
 GAA
 GBB
2

Gl.8
  G
kij  zij exp 
 RT


ij




Im Parameter zij steckt zusätzlich,
dass der ÜZ aufgeteilt ist, also
noch eine
Zusammenstoßhäufigkeit der
Teil-ÜZ zu berücksichtigen ist.

k AA  G AA
ln

z AA
RT

k BB  GBB
ln

z BB
RT

k AB  G AB
ln

z AB
RT
ln K AB
0
 G AB

RT
G

AB

1
0


  G AB
 G AA
 GBB
2

 k AB  1 
 k AA 
 k BB  
    ln K AB  ln 
  ln 
 
ln 


 z AB  2 
 z AA 
 z BB  
k AB
k AA k BB
 K AB 

z AB
z AA z BB
k AB  K AB  k AA  k BB  F
2
F
z AB
1
z AA  z BB
Zusammenhang zwischen G 0 und G  für eine Serie
verwandter Reaktionen:
Die Marcus-Theorie führt auf eine
quadratische Gleichung:

G 
G  1 

4
 

0
2
Der Parameter λ beschreibt die Umordnungsenergie
(reorganisation energy), die auf der Änderung von
Bindungsabständen und der Solvatation beruht. λ ist für all diese
verwandten Reaktionen gleich.

G 
G  1 
4
 

0
2
G  nimmt zunächst ab, wenn G 0 von Null zu einem negativen Wert
abnimmt (wie erwartet), die Reaktionsgeschwindigkeit steigt (normale Region)
G  0
Bei G   wird
Reaktionsgeschwindigkeit!
0

d.h.
Wird G noch negativer, so steigt G
die Reaktionsgeschwindigkeit sinkt wieder.
0
Maximum der

Marcus entwickelte seine Theorie 1956-1965.
wieder (inverser Marcus-Bereich),
• Ab 1970 Durchbruch der Marcus-Theorie, experimentelle
Bestätigungen
• Wird heute vielfach angewendet z.B. auf elektrolytische
Reaktionen, elektrisch leitfähige Polymere,
photochemische Prozesse, Photosynthese,
Chemilumineszenz, Korrosionsvorgänge u.a.
Redoxreaktionen, die in der inneren Sphäre
ablaufen
• ÜZ durch einen gemeinsamen Brückenliganden zwischen den beiden
Reaktionspartnern charakterisiert
• tritt in biologischen Systemen eher selten auf
• Wichtig beim Elektronentransfer von Übergangsmetallen in Lösung
1983 wurde der Nobelpreis an Henry Taube (19152005) verliehen - für die Beschreibung des
Elektronentransfers bei inner-sphere Redoxreaktionen
(Elektronentransfer von Übergangsmetallen in
Lösungen.) Seine theoretischen Modelle waren von
großer Bedeutung für die spätere Forschung.
Foto: http://news.stanford.edu/news/2005/november30/taube-113005.html
CrH O 
2
2
6
 CoNH3 5 Cl   5 H3O  CrClH 2O5   CoH 2O6   5 NH4
2
Diese Reaktion ist rasch, k=6x105 s-1mol-1L
Inner-sphere oder outer-sphere Mechanismus?
2
2
Verhalten gegenüber Liganden-Substitution:
Co(III) inert, Co(II) labil, Cr(III) inert, Cr(II) labil
1. Annahme: outer-sphere (?)
CrH O 
2
2
6
 CoNH3 5 Cl   direct e  transfer  CrH 2O 6   CoNH3 5 Cl 
2
CoNH  Cl

3 5
3

 5 H3O  H 2O  schnell  CoH 2O6   5 NH4  Cl 
2
CrH O 
3
2
6
 Cl   langsam  CrClH 2O5   H 2O
2
2. Annahme: inner-sphere
CrH O 
2
2
6
 CoNH3 5 Cl   Brückenmechanismus  CrClH 2O5   CoNH3 5 ( H 2O)
2
CoNH  H O
2
3 5
2
2
 5 H3O  schnell  CoH 2O6   5 NH4
2
Die Schlüsselfrage ist, ob die CrCl2+ Spezies
rasch (inner-sphere durch den
Redoxmechanismus)
oder langsam (outer sphere durch den
Liganden-Substitutionsschritt) gebildet wird.
2
Beweis für inner-sphere
Mechanismus:
Wird die CrCl2+ Spezies durch Ionenaustausch aus
dem Reaktionsgemisch abgetrennt und mit einer
UV-Methode bestimmt, so erkennt man, dass sie
wesentlich rascher entsteht als durch einfache
Liganden-Substitution.
Brücken  Zwischenverbindung
H O  Cr  Cl  CoNH  
4
2
5
3 5
Bedingung für einen inner-sphere
Mechanismus:
Der Brückenligand muss imstande sein,
als Lewis-Base (Elektronenpaardonator)
für zwei Metallatome gleichzeitig zu
dienen.
Wenn z.B. alle Liganden am inerten
Reaktanden NH3 sind, dann muss die
Reaktion nach einem outer-sphere
Mechanismus vor sich gehen, denn N hat
nur ein Paar nichtbindender Elektronen
keine
Brückenstruktur
möglich
Der outer-sphere Mechanismus ist ungünstiger,
denn zwischen dem Oxidations- und
Reduktionsmittel besteht keine Wechselwirkung,
die diesen helfen könnte, ihre Energien aneinander
anzugleichen, wie dies von der Franck-Condon
Bedingung gefordert wird!
Oxidation von Cr 2 mit CoNH 3 5 Cl 
2
um 10 Größenordnungen rascher
als mit Co NH 3 6 
3
Wo erfolgt der Angriff
wenn der Brückenligand mehrere Atome hat?
Cr H O    CrH O  X 
2
*
2
6
2
2
5

 Cr * H 2O 5 X
  CrH O  
2
2
2
6
für X=NCS- ist k=1,4x10-4 s-1mol-1L
für X=SCN- ist k=4x101 s-1mol-1L
(25°C)
Cr(H2O)52+ ist eine recht harte
Lewis-Säure: stabilere Bindung
mit N (harte Lewis-Base) als
mit S (weiche Lewis Base)
höhere Konzentration
an ÜZ im QuasiGleichgewicht wenn
X=SCN-
CoNH  NCS
2
3 5
 CrH 2O6  
2
ergibt ausschließlich das Cr-SCN2+ Produkt
d.h. der Angriff erfolgt am weiter entfernten Atom
remote attack
CoNH  SCN 
2
3 5
 CrH 2O6  
2
ergibt 30% Cr-SCN2+ d.h. Angriff am unmittelbar benachbarten Atom
adjacent attack
und 70% Cr-NCS2+
remote attack
Das angreifende Cr2+ hat eine
„Vorliebe“ für das S-Atom,
obwohl das Cr-SCN2+
thermodynamisch weniger stabil
ist als das Cr-NCS2+
WARUM?
Der Mechanismus des
Elektronentransfers
zerfällt in zwei Teilschritte
1.) Brücke wird reduziert
2.) Weiterleitung des e- auf das Oxidationsmittel
S lässt sich durch ein benachbartes Cr2+
leichter reduzieren als N.