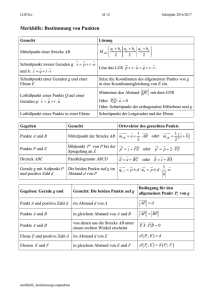
1 - Lehrerseite von Wolfram Thom
Werbung
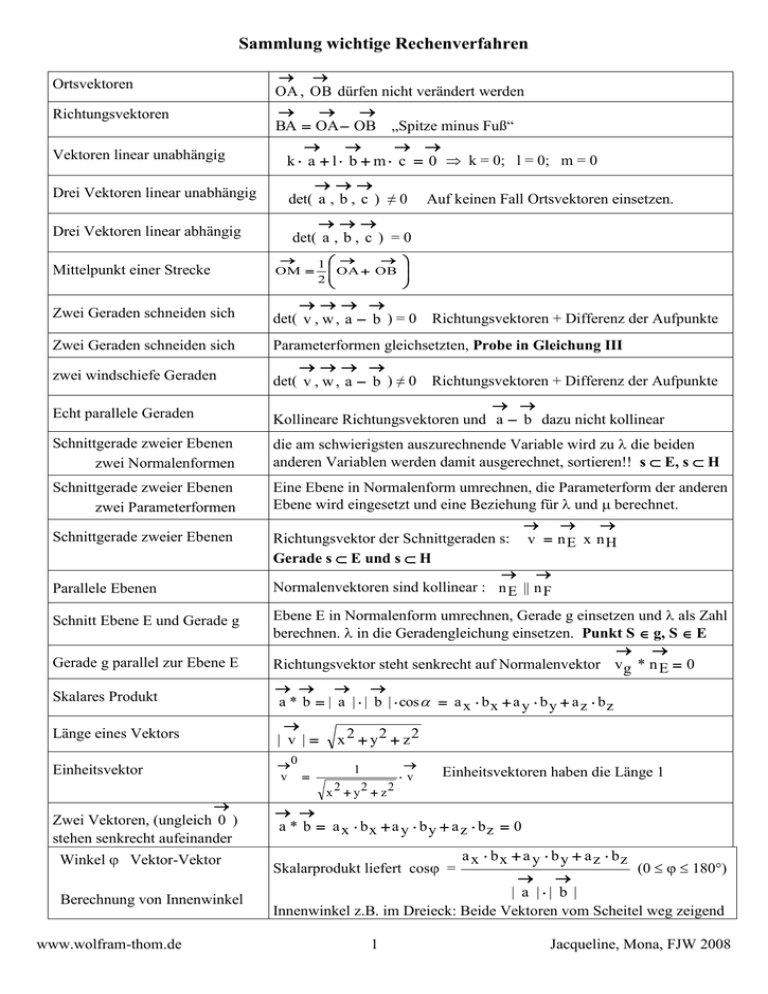
Sammlung wichtige Rechenverfahren Ortsvektoren Richtungsvektoren Vektoren linear unabhängig OA , OB dürfen nicht verändert werden BA OA OB „Spitze minus Fuß“ k a l b m c 0 k = 0; l = 0; m = 0 Drei Vektoren linear unabhängig det( a , b , c ) ≠ 0 Drei Vektoren linear abhängig det( a , b , c ) = 0 Auf keinen Fall Ortsvektoren einsetzen. Mittelpunkt einer Strecke 1 OM OA OB 2 Zwei Geraden schneiden sich det( v , w , a b ) = 0 Zwei Geraden schneiden sich Parameterformen gleichsetzten, Probe in Gleichung III zwei windschiefe Geraden det( v , w , a b ) ≠ 0 Echt parallele Geraden Kollineare Richtungsvektoren und a b dazu nicht kollinear Schnittgerade zweier Ebenen zwei Normalenformen die am schwierigsten auszurechnende Variable wird zu die beiden anderen Variablen werden damit ausgerechnet, sortieren!! s E, s H Schnittgerade zweier Ebenen zwei Parameterformen Eine Ebene in Normalenform umrechnen, die Parameterform der anderen Ebene wird eingesetzt und eine Beziehung für und berechnet. Richtungsvektor der Schnittgeraden s: v n E x n H Gerade s E und s H Normalenvektoren sind kollinear : n E || n F Schnittgerade zweier Ebenen Parallele Ebenen Schnitt Ebene E und Gerade g Gerade g parallel zur Ebene E Skalares Produkt Länge eines Vektors Einheitsvektor Zwei Vektoren, (ungleich 0 ) stehen senkrecht aufeinander Winkel Vektor-Vektor Berechnung von Innenwinkel www.wolfram-thom.de Richtungsvektoren + Differenz der Aufpunkte Richtungsvektoren + Differenz der Aufpunkte Ebene E in Normalenform umrechnen, Gerade g einsetzen und als Zahl berechnen. in die Geradengleichung einsetzen. Punkt S g, S E Richtungsvektor steht senkrecht auf Normalenvektor v g * n E 0 a * b | a | | b | cos a x b x a y b y a z b z | v | x 2 y2 z2 0 v 1 x 2 y2 z2 v Einheitsvektoren haben die Länge 1 a * b a x bx a y b y a z bz 0 a x bx a y b y a z bz (0 180°) | a || b | Innenwinkel z.B. im Dreieck: Beide Vektoren vom Scheitel weg zeigend Skalarprodukt liefert cos = 1 Jacqueline, Mona, FJW 2008 Winkel Gerade-Gerade Winkel Ebene-Ebene Winkel Ebene-Gerade Skalarprodukt der Richtungsvektoren. Das "Skalarprodukt im Betrag" liefert den kleineren der beiden Zwischenwinkel(0 90° ) Winkel zwischen den Normalenvektoren n n E und u n F nx ux n y u y nz uz cos = ; (0 90° ) | n || u | Winkel zwischen Richtungsvektor von g und Normalenvektor von E < 90° = 90° – > 90° = – 90° nE g E Spurpunkte einer Geraden Schnittpunkte mit Koordinatenebenen z.B. xy-Ebene: z = 0 ; Geradengleichung, einsetzen, berechnen Spurpunkte von Ebenen Schnittpunkte mit Koordinatenachsen; notwendig für Zeichnungen; 1 Ebene in Normalenform, z.B x-Achse x 0 einsetzen, Px berechnen 0 Spurgeraden von Ebenen = Schnittgerade einer Ebene mit den Koordinatenebenen, z.B. Spurgerade mit xy -Ebene: Ebene in Parameterform, z = 0 setzen in Abhängigkeit von berechnen Spurgerade Senkrechte Projektion einer Geraden in Koordinatenebene z.B. in xy -Ebene: Einfach in der Geradengleichung die z - Koordinaten auf Null setzen. Lotfußpunkt L eines Punktes P zur Ebene E Abstand Punkt P - Ebene E Normalenvektor n von E berechnen. Gerade h aus P und n aufstellen Schnittpunkt L von Gerade h und Ebene E berechnen. P in HNF einsetzen ergibt gerichteten Abstand d(P ,E), Betrag! Fläche eines Parallelogramms Länge des Vektorproduktes a x b Fläche eines Dreiecks Halbes Parallelogramm: Fläche eines Vierecks Fläche eines Fünfecks Volumen eines Spats Volumen eines Tetraeders Volumen einer Pyramide Vektorprodukt www.wolfram-thom.de 1 AB x AC 2 1 1 AB x AC AC x AD in zwei Dreiecke zerlegen: 2 2 1 1 1 AB x AC AC x AD AD x AE in drei Dreiecke zerlegen: 2 2 2 a x b*c (bzw. zyklisch vertauscht) oder det a, b,c det AB, AD, AE 1 V = a x b *c 6 V= V= 1 G h 3 a b a x b c a b u v bw cv w cu aw u av bu v 2 | a x b | | a | | b | sin Jacqueline, Mona, FJW 2008 1. Hessesche Normalenform Normalenvektor n berechnen, Einheitsvektor bilden. n 0 Vorzeichen des Normalenvektors n so, dass n * a 0 Ebenengleichung : n 0 * x n 0 * a 0 oder ax bx cx d a 2 b2 c2 0 wobei d n * a 0 und n b a c 2. Normalenvektor der HNF Zeigt im Ursprung eingezeichnet zur Ebene E hin Zeigt in der Ebene eingezeichnet vom Ursprung weg 3. Abstand Punkt P – Ebene E HNF E und Punkt P einsetzen. Achtung: gerichteter Abstand ! Betrag !! Zahl > 0: Punkt P und der Ursprung in verschiedenen Halbebenen Zahl < 0: Punkt P und der Ursprung in gleichen Halbebenen 4. Lotfußpunkt F eines Punktes P zur Ebene E P Normalenvektor n von E berechnen. Gerade h aus P und n aufstellen Schnittpunkt F von Gerade h und Ebene E berechnen. (Lotfußpunkt) 5. Abstand Punkt P - Ebene E 6. Spiegelung Punkt an Ebene F E P in HNF einsetzen ergibt gerichteten Abstand d(P ,E), Betrag! Lotfußpunkt F von P bestimmen (wie Nr.4) OP' OF PF OP 2 PF P oder Abstand d des Punktes von Ebene bestimmen F E 0 (Nr. 5), dann ist 0P ' 0P 2 d n , wenn d mit Vorzeichen eingesetzt wird 7. Spiegelung Gerade an Ebene Gerade g parallel zu E P' g und g' haben denselben Richtungsvektor. Es genügt den Aufpunkt A zu spiegeln (wie Nr.6) g A F E A' Spiegelung Gerade an Ebene Gerade g nicht parallel zu E Berechne Schnittpunkt S von E und g Schnittpunkt S gehört auch zu g', also einen weiteren Punkt A von g an E spiegeln (wie Nr.6) Gerade SA’ angeben A E www.wolfram-thom.de Punkt A als Aufpunkt auswählen, der Richtungsvektor w der Geraden g wird zum Normalenvektor: w * x w * a 0 3 S F A' 8. Orthogonalebene durch A zur Geraden g g' g' g L A Jacqueline, Mona, FJW 2008 9. Abstand paralleler Geraden g; h g: x = OA u und h: x = OB u Bilde die Orthogonalebene L durch den Aufpunkt A senkrecht g h A zum Richtungsvektor u von g. Bestimme den Schnittpunkt C von L und h Die Länge des C L Verbindungsvektors AC ist der gesuchte Abstand. 10. Abstand Punkt P – Gerade g Gerade g: x = OA u Orthogonalebene L: Richtungs A vektor u von g = Normalenvektor n von L mit Aufpunkt P. S L: u * x u * p 0 Ebene L mit g schneiden Punkt S Vektor SP Die Länge des Vektors | SP | ist der kürzeste Abstand 11. Abstand zweier windschiefer Geraden g und h x = OA u 12. Abstand zweier windschiefer Geraden g und h gemeinsamen Lotvektor berechnen: v u x w Gerade g; x = OA u Gerade h: x = OB w L h x = OA u w Gerade h: x = OB w Punkte S und T des kürzesten Abstands P Ebene E aufstellen, die g enthält und parallel zur Gerade h ist E: HNF von E bestimmen Punkt B in die HNF von E einsetzen, dies liefert den gerichteten Abstand Gerade g; g h Ebene F aufstellen, die Gerade g und v enthält, Normalenform von F! Gerade h mit Ebene F schneiden Schnittpunkt S F Lotgerade m aufstellen mit Aufpunkt S und T g Lotvektor v . Berechne Schnittpunkt T der Lotgeraden m mit Gerade g. Vektor ST Die Länge des Vektors | ST | ist der kürzeste Abstand S W1/2 = HNF E HNF F 14. Winkelhalbierende von zwei Geraden g und h Schnittpunkt S = g h berechnen = Aufpunkt www.wolfram-thom.de E d 13. Winkelhalbierende Ebenen 15. Teilpunkt einer Strecke AB g 0 Richtungsvektor s 1/2 = u AT t TB 0 w t > 0 innerer Teilpunkt t < 0 äußerer Teilpunkt 4 (Siehe Formelsammlung) Jacqueline, Mona, FJW 2008