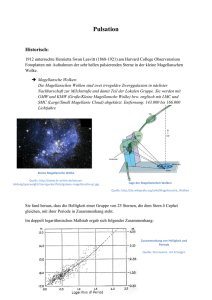
AB_Helligkeit
Werbung

Arbeitsblatt Helligkeit - Astronomie Seite 1 Graf-Zeppelin-Gymnasium Arbeitsblatt: Helligkeit der Sterne Inhaltsverzeichnis: Arbeitsblatt 6: Helligkeit der Sterne ................................................................................................ 1 6.1 Visuelle Helligkeit - Zusammenhang Helligkeit und Energie .............................................. 1 6.2 Absolute Helligkeit - Zusammenhang Helligkeit und Entfernung ........................................ 4 6.3 Lösungen der Aufgaben ........................................................................................................ 6 1 Visuelle Helligkeit - Zusammenhang Helligkeit und Energie 1. Wenn ein Stern Energie in Form von Licht zur Erde schickt, empfindet der Mensch dies als Helligkeit. Um so mehr Energie der Stern pro Sekunde zur Erde schickt, um so heller erscheint uns der Stern. Nun gilt aber nicht, dass ein Stern, der doppelt so viel Energie pro Sekunde zur Erde schickt, wie ein anderer Stern, uns doppelt so hell erscheint. Um den Zusammenhang dieser beiden Größen Energie (besser Empfangsleistung pro Fläche) und Helligkeit zu verstehen, müssen wir einige komplexere Dinge durchdenken. 2. Die Astronomie ist eine alte Wissenschaft. Das, was man heute visuelle Helligkeit der Sterne nennt, ist im Kern vor rund 2500 Jahren entstanden. Die Griechen gruppierten die Sterne nach ihrer Helligkeit. Vereinfacht gesprochen: Sie unterteilten die Sterne in 7 Gruppen, Sterne der Helligkeit 0 waren ganz helle Sterne, Sterne der Helligkeit 1 weniger helle und Sterne der Helligkeit 6 waren die Sterne, die nur ganz schwach zu sehen waren. Wenn ein Stern etwa zu Gruppe 3 gehört, sagt man, er ist von 3. Größe. 3. Daraus ist die visuelle Helligkeit m oder Magnitude entstanden. Die Einheit der Helligkeit nennt man mag (sprich mag oder magnitudo). Es gibt heute auch Sterne der Helligkeit 3,5 mag oder 2,02 mag. Oft wird auch 2,02m oder 2,m02 geschrieben. Man hat die Gruppierung der Griechen durch eine Ordnung gemäß der Helligkeit ersetzt. Der Polarstern hat also die Helligkeit m = 2,02 mag (es gibt auch Quellen mit 2,12 mag oder 1,97 mag (Wikipedia)). Das für uns heutige Menschen Überraschende ist aber, dass eine große Helligkeitszahl heißt, der Stern ist nur schwach zu sehen, ist also nicht hell, sondern leuchtet nur schwach; um so größer die Helligkeit ist, um so kleiner ist die visuelle Helligkeitszahl m. Merke: Die Maßzahl der visuellen Helligkeit steigt, wenn die Helligkeit sinkt! 4. Die Sonne hat die Helligkeit -26,8 mag, Sirius im kleinen Hund, der hellste Stern am Himmel, hat die Helligkeit m = -1,45 mag, der Polarstern hat die Helligkeit 2,05 mag. Wega im Sternbild Leier hat die Helligkeit 0,03 mag. Sterne, die man bei guten Bedingungen gerade noch sieht, haben ungefähr die Helligkeit 6 mag. Unter Großstadtbedingungen sieht man meist nur Sterne bis zur 4. Größe. Mit Fernrohren kann man heutzutage Sterne etwa bis zur Helligkeit von 30 mag sehen. 5. Sterne senden Licht aus. Licht ist Energie. Unser Auge und die Photoplatten oder CCDs der Astronomen reagieren nun auf empfangene Energie pro Fläche. Die Helligkeit ist groß (d.h. die Zahl m ist klein!), der Stern ist gut sichtbar, wenn die pro Sekunde empfangene Energie pro Fläche groß ist, die vom Stern ausgehend bei uns ankommt. Die Energie pro Fläche und Sekunde bezeichnen wir im Folgenden mit p, es ist eine Leistungsdichte, Leistung/Fläche oder Energie pro Zeit und pro Fläche. Wir nennen sie Strahlungsdichte. (oder Flussdichte, Strahlungsflussdichte). Wir halten fest: Das, was die Helligkeit bestimmt, ist die Energie, die ein Stern pro 1/50 Sekunde in unser Auge strahlt, also E = p*1/50s*Augenfläche. Fernrohre können auf zwei Arten mehr Energie von den Sternen sammeln: Einmal indem sie einen Stern lange beobachten (lange Belichtungszeit, oft über Stunden) und dann indem sie die Energie, die auf das ganze Fernrohr auffällt, auf einer kleinen Fläche sammeln (die Fernrohre haben also eine möglichst große Öffnung, der Durchmesser der Fernrohre ist 5 m oder 8 m!. Sie 579891726 W.Seyboldt Stand: 1.9.08 Arbeitsblatt Helligkeit - Astronomie Seite 2 Graf-Zeppelin-Gymnasium sehen deshalb auch Sterne, die wir mit unseren Augen nicht mehr sehen können, sie sehen z.B. Sterne bis zur der Helligkeit m = 31 mag (Hubble-Teleskop) 6. Aufgabe: Unser Auge hat normalerweise im Halbdunkeln einen Durchmesser von 4mm, bei langer Adaptation (15-30 min) kann der Durchmesser 8 mm betragen. Benutze die Formel also E = p*1/50s*Augenfläche, um das Energieverhältnis E1 /E2 zu bestimmen, wenn E1 die Energie ist, die das Auge im Halbdunkeln empfängt und E2, das, das es bei langer Adaptation empfängt. Bestimme ebenso das Verhältnis E1 / E3 wenn E3, die Energie ist, die ein Teleskop von 5 m Durchmesser bei einer Belichtungszeit von 5 h empfängt. 7. Jeder weiß, dass eine Lampe, die sich entfernt, weniger hell erscheint. Wie beeinflusst nun die Entfernung einer Lampe ihre Strahlungsdichte p? Die Energie, die eine Lampe (oder ein Stern) pro Sekunde ausschickt, verteilt sich mit steigender Entfernung auf eine immer größere Kugeloberfläche. Damit sinkt die Strahlungsdichte mit steigender Entfernung so stark, wie die Kugeloberfläche sich vergrößert. Die Energie, die vom Stern pro Sekunde ausgestrahlt wird, verteilt sich ja auf eine immer größere Fläche, also wird die Energie pro Fläche mit steigender Entfernung immer kleiner. Die Oberfläche einer Kugel ist O 4r 2 . Damit verteilt sich die Energie bei doppelter Entfernung vom Stern auf die vierfache Fläche, die Strahlungsdichte fällt also auf ¼. 8. Ganz konkret: Wir betrachten zwei Lampen A und B. A sei r km von uns entfernt (etwa r = 2,3 km), B sei n*r km von uns entfernt (etwa 7*r=16,1 km). Beide Lampen sollen pro Sekunde dieselbe Strahlungsenergie aussenden, d.h. dieselbe Energie P (die insgesamt in jede Richtung abgestrahlte Energie, nicht die Strahlungsdichte p) abstrahlen. Die P Strahlungsdichte des Sterns A bei unserem Auge ist dann p A , die des Sterns B 4r 2 P P 1 P 1 pB 2 2 pA . D.h., wenn die Entfernung eines Sterns B 7 2 2 2 2 4 (xr) 4 x r x 4r x 1 mal so groß ist wie die des Sterns A, so ist die Strahlungsdichte nur noch der von A 49 (x ist dann ja 7). Man sagt, die Strahlungsdichte sinkt quadratisch mit der Entfernung: x1 fache Entfernung bedeutet Multiplikation der Strahlungsdichte mit dem Faktor 2 . x 2 r p Es gilt A x 2 B , d.h. die Strahlungsdichten verhalten sich umgekehrt wie die pB rA Quadrate der Entfernungen. Ist der Stern 1 x mal so weit von uns entfernt, wie Stern 2, so ist die Strahlungsdichte von Stern 1 nur 1/x2 der von Stern 2, wenn beide gleich viel Licht aussenden. Wenn die Strahlungsdichte von Stern 1 y mal so hoch ist, wie die von Stern 2, dann ist Stern 2 y so weit von uns entfernt, wie Stern 1, wenn beide gleich viel Licht aussenden. 9. Aufgabe: Wega in der Leier (der 5.-hellste Stern am Himmel) ist 25,3 Lj von uns entfernt. Rigel im Orion ist 770 Lj von uns entfernt. Was gälte für das Strahlungsverhältnis der beiden Sterne, wenn sie gleich viel Energie abstrahlen würden? 10. Als man die Strahlungsleistungen der Sterne gemessen hat, hat man festgestellt, dass die Strahlungsleistung der Sterne, deren visuelle Helligkeit 5 Größenklassen höher ist als die ihrer helleren Gefährten, nur 1/100 der helleren Sterne ist. Allgemeiner: Immer wenn die 579891726 W.Seyboldt Stand: 1.9.08 Arbeitsblatt Helligkeit - Astronomie Seite 3 Graf-Zeppelin-Gymnasium Strahlungsleistung auf 1/100 fällt, dann muss zur visuellen Helligkeit 5 dazu addiert werden. 11. Biologen haben allgemein festgestellt: Wenn ein Reiz physiologisch (die Helligkeit reizt unsere Photorezeptoren im Auge) doppelt so stark empfunden wird, als ein anderer, so ist die den Reiz auslösende physikalische Größe in der Regel auf ein Mehrfaches angewachsen, z.B. auf das Fünffaches (es muss nicht das Doppelte oder Vierfache sein). Bei den Sternen heißt das konkret, wenn die Helligkeit auf das Hundertfache (multiplikativ) angewachsen ist, so haben die Menschen den Eindruck, dass die visuelle Helligkeit um 5 Helligkeitsstufen (additiv) abgenommen hat (größere Zahlen, kleinere Helligkeit). In der Mathematik lernt man, dass das Multiplizieren von Potenzen bedeutet, dass die Exponenten addiert werden: a n a m a n m . Der Zusammenhang zwischen der von den Menschen empfundenen visueller Helligkeit m und der der physikalischen Strahlungsleitung p sollte also durch eine Wachstumsfunktion (Exponentialfunktion) beschreiben werden, durch eine Funktion der Gestalt f : m p c a m (m = Helligkeit, p = Strahlungsdichte). Dann gilt: Wenn ich jetzt zu m eine Zahl x addiere, dann heißt das, dass p mit der Zahl ax multipliziert wird ( c a m x c a m a x c a m a x p a x ) 12. (Bem: Die Abschnitt 12) bis 14) sind mathematisch schwerer. Wer möchte, kann sie überlesen und nur das Ergebnis in 15) lernen) Wollen wir nun wissen, wie man damit zu einem gegebenen p das zugehörige m bestimmt, so müssen wir die Gleichung p c a m nach m auflösen (mathematischer. Wir benötigen die Umkehrfunktion). Wir dividieren beide Seiten der Gleichungen durch c und nehmen dann auf beiden Seiten den Logarithmus. p Damit erhalten wir lg lg a m m lg a oder c 1 1 1 p m lg lg p lg c k lg(p) r . lg a c lg a lg a 1 1 und r lg c . lg a lg a Zusammenfassung: Es gibt Zahlen k und r, so dass die Helligkeit m sich mit der Formel m k lg(p) 1 aus der Strahlungsdichte des Sterns berechnen lässt. Die Zahlen k und r müssen dabei geeignet angepasst werden, siehe unten, Punkt 13) 13. Das ist ein Beispiel für das allgemeine Weber-Fechner-Gesetz. Es besagt, dass sich die subjektive Stärke von Sinneseindrücken logarithmisch zur objektiven Intensität des physikalischen Reizes verhält. Um die Größe eines Reizes zu bestimmen, sollte man also die physikalische Größe als aReiz schreiben können. Dieses biologische Empfinden hat den Vorteil, dass Reize mir großer Bandbreite verarbeitet werden können. Wenn sich die physikalische Größe etwa verfünffacht, so verdoppelt sich der Reiz nur - oder wenn sich die physikalische Grüße vertausendfacht, dann steigt ein anderer Reiz nur auf das 10fache. Dabei haben wir einfach zur Abkürzung festgelegt: k 14. Wie hängt nun die visuelle Helligkeit konkret mit der Strahlungsdichte zusammen? Wir wissen, wenn die Differenz der visuellen Helligkeiten 5 ist, so ist der Quotient der zugehörigen Strahlungsdichten 1/100. Also gilt: Wenn m1 um fünf Helligkeitsstufen größer ist als m2, so ist die Strahlungsdichte des Sterns 2 (der mit der kleineren Helligkeitszahl ist ja heller) 100 mal größer als die des Sterns 1, d.h. es gilt p1 / p2 = 1/100 . Also ergibt sich mit der Formel von 12) 579891726 W.Seyboldt Stand: 1.9.08 Arbeitsblatt Helligkeit - Astronomie Seite 4 Graf-Zeppelin-Gymnasium p 5 m1 m 2 k lg p1 r k lg p 2 r k lg p1 lg p1 k lg 1 p2 1 k lg k 2 100 Damit muss k = -2,5 sein. p E 15. Es gilt also m1 m2 2,5 lg 1 2,5 lg 1 wenn m1 und m2 die visuellen p2 E2 Helligkeit der Sterne 1 und 2 und E1 und E2 die von den Sternen abgestrahlte Energie ist. Bem.: Die Astonomen benutzen statt p meist E. Es gilt E = p * (bestrahlte Fläche) * Belichtungszeit. Also ist für jedes Fernrohr, jedes Auge p1 / p2 = E1 / E2. 16. Da man mit den CCDs eigentlich nur den Quotienten E1 / E2 bestimmen kann und nicht die absolute Größe von E, interessiert sich niemand für die Zahl r in der Formel von Punkt 12). Man vergleicht in der Praxis einfach die Energiemenge eines unbekannten Sterns mit dem eines bekannten auf der Aufnahme und addiert dann die mit der gerade abgeleiteten Formel erhaltene Differenz der Zahlen m zur bekannten Helligkeit des Referenzsterns. Lange Zeit hat man immer möglichst den Polarstern als Referenzstern genommen – inzwischen hat man aber festgestellt, dass dieser Stern seine Helligkeit immer wieder ändert (wenn auch nur minimal). Wir merken uns trotzdem, dass man seine Helligkeit von m = 2,12 mag als Bezugspunkt nehmen kann. 17. Aufgabe: Der Polarstern hat eine Helligkeit von mPolarstern = 2,02. Die Strahlungsdichte von ihm ist 14,86 mal so groß wie die vom dunkelsten Stern des kleinen Bären (η-UMi). Welche visuelle Helligkeit hat dieser Stern?, d.h. heißt, wie hell wäre er, wenn er in derselben Entfernung wäre wie der Polarstern? 18. Aufgabe: Der Polarstern hat eine Helligkeit von mPolarstern = 2,02 mag – der Stern Wega hat eine Helligkeit von mWega = 0,03 mag. Berechne (mit der Formel von Punkt 15), wie viel mal mehr Energie (pro Zeiteinheit s und pro Flächeneinheit) in Form von Licht die Wega zur Erde sendet als der Polarstern. 19. Aufgabe: Was ergibt sich, wenn wir die Sonne (mSonne = -26,8 mag) mit dem Polarstern vergleichen? 20. Aufgabe: Wie groß ist der visuelle Helligkeitsunterschied, wenn Stern 1 auf der Erde eine 10 mal (doppelt, 100 mal) so große Strahlungsdichte hat, wie Stern 2? 21. Aufgabe: Wie viel mal höher ist die Strahlungsdichte von Stern 1, wenn Stern 1 eine um 1 Einheit kleinere Helligkeitsstufe hat als Stern 2? 2 Absolute Helligkeit - Zusammenhang Helligkeit und Entfernung 22. Die visuelle Helligkeit m, die Strahlungsdichte auf der Erde, sagt nichts aus über die vom Stern abgestrahlte Leistung, über die pro Zeit abgestrahlte Energie. Die Helligkeit nimmt ja mit steigender Entfernung des Sterns von der Erde ab, siehe Punkte 6 und 7. 23. Die Energie, die der Stern abstrahlt, verteilt sich über eine Kugeloberfläche. Da die Kugeloberflache ( O 4r 2 ) bei Verdopplung des Radius auf das 4-fach steigt, fällt die Strahlungsdichte p, die Energie pro Zeit und pro Fläche, die auf der Erde ankommt auf 579891726 W.Seyboldt Stand: 1.9.08 Arbeitsblatt Helligkeit - Astronomie Seite 5 Graf-Zeppelin-Gymnasium ein Viertel, wenn sich der Abstand eines Sterns verdoppelt. Damit gilt für die visuelle 1 Helligkeit von zwei gleich hellen Sternen: m 2 m1 2,5 lg 1,505 , wenn Stern 2 4 doppelt so weit von der Erde entfernt ist, wie Stern 1. 24. Aufgabe: Was gilt für die visuelle Helligkeit von zwei gleich hellen Sternen, wenn der eine 3,4 mal (350 mal) so weit von uns entfernt ist wie der andere? 25. Um die wirkliche Helligkeit der Sterne vergleichen zu können, hat man die absolute Helligkeit M eingeführt, das ist die Helligkeit, die der Stern hätte, wenn er 10 pc von der Erde entfernt wäre. Wenn zwei Sterne dieselbe absolute Helligkeit haben, dann strahlen sie in gleichen Zeiten gleich viel Energie ab. 26. Was gilt für die Helligkeit m10pc, wenn wir einen Stern der Helligkeit m aus der Entfernung von r pc in eine Entfernung von 10 pc verschieben? (Zur Erinnerung: 1 pc = 3,26 Lj, die Entfernung, unter der der Erdbahnradius unter einem Sichtwinkel von 1’’ = 1/3600° erscheint) Bestimme zuerst das Verhältnis der Oberfläche einer Kugel mit Radius 10 pc zu einer mit 100 r pc. (Lösung: 2 ). r Da sich die Strahlungsdichte in der Entfernung von 10 pc im Vergleich zu der in einer Entfernung von r pc umgekehrt wie ihre jeweiligen Kugeloberflächen verhalten, gilt E rpc 100 2 damit für E10pc r Mit der Formel von Punkt 3 gilt dann E10pc E rpc 100 m10pc m rpc 2,5 lg 2,5 lg 2,5 lg 2 E rpc E10pc r 2,5 lg(100) lg(r 2 ) 2,5 2 2,5 2 lg(r) 5 5 lg(r) oder: m10pc m rpc 5 5 lg(r) (siehe auch Folie 5 von AstroF_Helligkeit.ppt) 27. Da die absolute Helligkeit M die visuelle Helligkeit m ist, die der Stern hätte, wenn man x ihn aus einer Entfernung von r pc = Lj in eine Entfernung von 10 pc bringt, gilt 3, 26 damit M m 5 5 lg(r) 28. Aufgabe: Berechne die fehlenden Werte der Tabelle von Folie 6 der PPP AstroF_Helligkeit.ppt 29. Aufgabe: Wie weit ist der Stern Rigel von der Erde entfernt, wenn er eine scheinbare Helligkeit von m = 0,12 mag und eine absolute Helligkeit von M = -6,78 Mag hat? 579891726 W.Seyboldt Stand: 1.9.08 Arbeitsblatt Helligkeit - Astronomie Seite 6 Graf-Zeppelin-Gymnasium 3 Lösungen der Aufgaben 2 r p Lösung von Aufgabe 9: Laut 8) gilt: A x 2 B Also ist (p von Rigel) / (p von Wega) pB rA 2 rWega 27,3 2 0, 00108 0,1% D.h. die Strahlungsdichte der Strahlung von Wega = rRigel 770 würde auf 0,1% seiner jetzigen Strahlungsdichte fallen, wenn Wega an die Position von Rigel vorschoben würde. Lösung von 17: Das Verhältnis der Strahlungsdichten ist = E Bär 1 also gilt E Polar 14,86 p E 1 mBär mPolar 2,5 lg Bär 2,5 lg Bär 2,5 lg 2,93 Also ist 14,86 pPolar E Polar mBär mPolar 2,93 2,02 2,93 4,95 mag Lösung von Aufgabe 18: Die Differenz der visuellen Helligkeiten ist mPolar - mWega = 1,99 E E 1,99 0, 796 . Damit ist Also gilt 1,99 2,5 lg Polar . Oder lg Polar E Wega E Wega 2,5 E Polar 100,796 0,16 16% . Damit sendet der Polarstern pro Sekunde nur 16% der Energie E Wega zur Erde wie Wega. Wega sendet dann 1/0,16 = 6,25 mal so viel Licht zur Erde wie der Polarstern. (Der Polarstern ist also mindestens 6, 25 2,5 mal weiter weg als Wega oder dunkler als Wega.) Lösung von Aufgabe 19: Die Sonne sendet 337 Milliarden mal mehr Energie zur Erde als der Polarstern.). Lösung von Aufgabe 20: Wenn E1 / E2 = 10 ist so ist m1 = m2 – 2,5 / wenn E1 / E2 = 2, so ist m1 = m2 – 0,753 / wenn E1 / E2 = 100 ist so ist m1 = m2 – 5) Lösung von Aufgabe 21: Ist m1 = m2-1, dann E1 / E2 = 2,512 1 2, 457 / bzw. 12, 72 Lösung von Aufgabe 24: m2 m1 2,5 lg 2 3, 4 579891726 W.Seyboldt Stand: 1.9.08