Astronomie: Koordinaten
Werbung

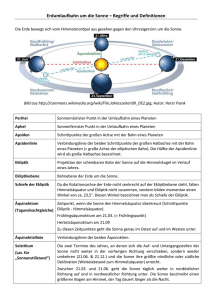
Arbeitsblatt Koordinatensysteme - Astronomie Seite 1 Graf-Zeppelin-Gymnasium Arbeitsblatt: Koordinatensysteme Inhaltsverzeichnis: Arbeitsblatt: Koordinatensysteme ................................................................................................... 1 1 Beobachtungsort Nordpol - Einführung ................................................................................... 2 2 Beobachtungsort Nordpol – Beobachtung mit CDC ................................................................ 4 3 Zusammenfassung Äquatorkoordinaten am Nordpol .............................................................. 5 4 Rotierende Äquatorkoordinaten an einem anderen Beobachtungsort ...................................... 8 5 Feststehende Äquatorkoordinaten .......................................................................................... 11 6 Sternzeit .................................................................................................................................. 11 7 Einen Stern mit Hilfe der Koordinaten RA und DE finden. .................................................. 15 8 Sternzeit und Umrechnungen der Koordinaten ...................................................................... 16 9 Analemma .............................................................................................................................. 18 10 Präzession der Erde .............................................................................................................. 19 Im Folgenden wollen wir uns die (rotierenden) Äquatorkoordinaten erarbeiten, mit denen jede Sternposition unabhängig vom Beobachtungsort und von der Beobachtungszeit beschrieben wird - sofern sich die Zeiten nur um wenige Jahre unterscheiden, siehe unten, Präzession der Erdachse. Diese Äquatorkoordinaten bestehen aus der Rektaszension RA = α (dem Winkel auf dem Himmelsäquator von Süden nach links, d.h. nach Osten, gedreht!) und der Deklination DE = δ (dem Drehwinkel vom Horizont nach oben in Richtung Zenit) – siehe Skizze unten 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 2 Graf-Zeppelin-Gymnasium 1 Beobachtungsort Nordpol - Einführung a) Wenn wir uns auf dem Nordpol befinden, ist der Zenit der Himmelnordpol (NCP North Celestial Pole in der unteren Skizze), der Punkt der Himmelskugel, zu dem die Erdachse zeigt, der Punkt, an dem wir den Polarstern sehen. Der Horizont ist der Himmelsäquator, die Linie, die man erhält, wenn man den Äquator an den Himmel projiziert. Erklärung der Skizze: NCP: North Celestial Pole (Himmelsnordpol, Position des Polarsterns) Celestial equator: Himmeläquator = der Schnittkreis, den die Äquatorebene der Erde mit dem Sternenhimmel bildet. Rektaszension α (right ascension) und Deklination δ (declination) (Widderpunkt, liegt inzwischen im Sternbild Fische) = Frühlingspunkt, Schnitt der Äquatorebene mit der Sonnenbahn = Stand der Sonne zu Beginn des Frühjahrs b) Der Punkt an dem die Sonne am Frühlingsanfang steht (etwa 21. 3. - genauer zu dem Zeitpunkt, an dem die Sonnenmitte am Horizont des Nordpols steht), nennt man Frühlingspunkt. ER wird mit dem Symbol des Widders bezeichnet. Stelle bei Stellarium den Nordpol ein, klicke die Atmosphäre weg, wähle als Uhrzeit den 20.3.12 um 6:14 (siehe http://de.wikipedia.org/wiki/Fr%C3%BChlingsanfang) und suche die Sonne (sie steht im Osten) Der Mittelpunkt der Sonne steht genau am Horizont. Sie steht im Führlingspunkt, leicht unterhalg von Pegasus. Gehen wir senkrecht hoch, so kommen wir etwa zu Caph in Kassipopeia. Wir zählen nun die Tage hoch und beobachten, wie die Sonne immer höher und die Steren sich nach rechts bewegen. Bemerkung: Der merkwürdige Sprung vom 24. auf den 25.3 kommt von der Einführung der Sommerzeit. Der Tag hat am letzten Sonntag im Jahr nur 23 Stunden, d.h. 6 Uhr ist eine Stunde früher! Die Sonne und die Sterne springen also um 15° nach links. Mitte Juni steht die Sonne oberhalb des Sternbilds Orion, Anfang August in den Zwillingen, Ende August im Löwen. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 3 Graf-Zeppelin-Gymnasium c) Wir führen nun neue Koordinaten ein: Rektaszension und Deklination. Am Nordpol der Erde stimmt die Deklination δ eines Sterns mit der Höhe des Sterns überein, d.h. mit der zweiten lokalen Horizontkoordinate. Die Rektaszension α ist im Prinzip dasselbe wie der Azimut, allerdings wird sie nach links (nicht nach rechts) größer und der Nullpunkt der Rektaszension ist nicht mehr Süden (wobei Süden am Nordpol eh nicht definierbar ist!), sondern ein Punkt auf dem Horizont des Nordpols. Dieser Punkt ist der Frühlingspunkt ♈, der Schnittpunkt der Sonnenbahn mit dem Himmelsäquator, der Punkt an dem die Sonne am Frühlingsanfang steht, dies ist meist der 20. März. Der Frühlingsanfang ist der Tag im Jahr, an dem der Mittelpunkt der Sonne am Nordpol genau auf dem Horizont steht. d) Genau genommen ist der Frühlingspunkt einer der beiden Punkte, an dem die Ekliptik (die Sonnenbahn) die Äquatorebene schneidet. Deshalb beginnt der Frühling nicht immer am gleichen Tag und deshalb kann man auch eine Uhrzeit für den Frühlingsbeginn angeben, siehe http://de.wikipedia.org/wiki/Frühlingsbeginn. Im Übrigen bewegt sich dieser Punkt im Lauf der Jahre langsam aufgrund der Präzession der Erdachse in die Richtung, in die sich die Erde dreht. In 25800 Jahren umrundet er einmal den Himmeläquator. Da der Frühlingspunkt das Jahr bestimmt, bedeutet dies, dass die die Sternbilder sich relativ zum Frühlingspunkt zurückbewegen – Der Frühlingspunkt wandert im Band der Tierkreisbilder nach vorne, also nimmt der Abstand des Steinbocks zum Frühlingspunkt laufend zu, d.h. die Sonne steht immer früher im Steinbock. Heute sind die Sterne im Vergleich zu vor 2150 Jahren etwa ein Zwölftel auf der Erdbahn zurück geblieben. Quelle. http://members.chello.at/planetensystem/st.htm e) Wir werden uns im Folgenden die Bewegung der Sterne am Nordpol nochmals mit Skychart veranschaulichen und sehen: Der Polarstern steht im Lauf eines Jahres immer (zumindest für einige Jahre) im Zenit, die Sterne bewegen sich innerhalb von 23h 54min und 4s einmal in stets gleicher Höhe um den Polarstern. Und: Kein Stern am Nordpol 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 4 Graf-Zeppelin-Gymnasium geht auf, keiner unter. Alle Sterne sind am Nordpol zirkumpolar, d.h. sie sind immer am Himmel zu sehen (falls es dunkel ist). 2 Beobachtungsort Nordpol – Beobachtung mit CDC a) Starte SkyChart, wähle als Sternwarte den Nordpol (etwa Icon am linken Rand oben, dann unter Favoriten wählen). Wähle die Zeit 20.3. um 12:30 (etwa Icon ). Blicke in den Zenit mit „Süden“ (dort wo es nach FN geht!) unten, so dass du den ganzen Himmel siehst: Klicke dazu zuerst auf das Icon und dann auf am recht Bildrand. Du kannst Dir vorstellen, du „lägest im Schnee“ und blickst nach oben in den Zenit. Der Polarstern steht direkt im Zenit, der „Süden“ (FN) ist dort, wo Deine Füße sind, der „Norden“ ist bei deinen Haaren. Schalte den Nachthimmel ein (Icon Himmelsfarbe wechseln ) Suche den großen Wagen, den Polarstern und Kassiopeia. Klicke notfalls nochmals auf das Icon S, so dass die Sonne „unten“ steht. Es ist Mittag sie steht also im Süden, besser dort wo für uns in FN Süden wäre. Das es Sommerhalbjahr ist, ist die Sonne am Nordpol übrigens den ganzen Tag zu sehen. b) Animiere mit ungefähr der Zeitdauer 2-5 min und beobachte einen Simulationstag lang den Himmel. Notiere Deine Beobachtungen im Heft. War Dir das beobachtete Verhalten schon bekannt, evtl. aus dem Erdkundeunterricht? (Kontrolle siehe i) – zeige mit der Maus auf Symbol i) bei der Kontrolle. c) Nochmals konkreter: In welche Richtung drehen sich die Sterne? Notiere Deine Beobachtung im Heft. (Kontrolle siehe ii) d) Wir animieren jetzt mit 23h 56 min, d.h. 1 Siderischen Tag. Was fällt Dir auf? Notiere Deine Beobachtungen im Heft. Kanntest Du das beobachtete Verhalten z.B. aus dem Erdkundeunterricht? (Kontrolle siehe iii) e) Wann wandert das Zentrum der Sonne vom grünen Bereich in den schwarzen, d.h. wann geht die Sonne auf? Wann geht sie unter. Notiere Deine Beobachtung im Heft. (Kontrolle siehe iv) f) Die Bahn, die die Sonne am Sternenhimmel (scheinbar) zurücklegt, nennt man Ekliptik. Arbeitsauftrag: Skizziere die Ekliptik und den nördlichen Sternenhimmel mit den wichtigsten Sternbildern im Heft. Wenn Du selbständig arbeiten möchtest, dir das zutraust, kannst Du die folgenden Textzeilen erst später lesen, die einen Vorschlag für eine Vorgehensweise enthalten. i. Vorschlag: Zeichne mit einem Zirkel einen großen Kreis in dein Heft, dies ist der bei CDC schwarz gezeichnete Mittelteil, d.h. der Teil des Himmels, der am Nordpol zu sehen ist. Wähle bei CdC den 20.3. morgens um 6 Uhr, blicke nach oben zum Pol, so dass der „Süden“ (das ist hier die Linie, die nach Friedrichshafen zeigt) unten ist (klicke dazu am linken Rand zuerst auf das Icon und dann auf . Die Sonne steht nun links. Lege das Blatt Papier quer und zeichne auf dem Kreisrand links die Sonne ein und dann Pegasus, Andromeda, Kassiopeia, den kleinen und großen Wagen (klicke notfalls bei CDC auf das Icon , so dass die Sternhilfslinien angezeigt werden). Der Polarstern steht im Mittelpunkt des Kreises. Oben am Kreis zeichnest Du Orion, Zwillinge, 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 5 Graf-Zeppelin-Gymnasium Fuhrmann, den kleinen Hund mit Prokyon. Rechts den Löwen, Jungfrau und Bärenhüter, links unten den Schwan, die Leier und den Adler. ii. Den Steinbock und den Wassermann zeichnest Du außerhalb des Kreises, ebenso die Waage (wenn Du auf rechts am Rand auf das Icon E klickst, dreht sich die Karte, so dass Du auch die Sterne im Süden und im Norden unterhalb des Horizontes findest, jetzt rechts bzw. links). iii. Zeichne den Frühlingspunkt ein - er ist der Punkt, an dem die Sonne am 20.3. steht. Dieser Punkt dreht sich innerhalb von 23 h 56 min einmal entgegengesetzt zum Uhrzeigersinn um den Pol. iv. Wenn man die Sonnenbahn, d.h. die Bahn, auf der sich die Sonne im Lauf eines Jahres (von der nur die sommerliche Hälfte am Nordpol zu sehen ist) zeichnen möchtest, so genügt es drei oder vier weitere Punkte einzuzeichnen und sie dann einfach „rund“ zu verbinden. Wie aber findet man die weiten Punkte? Erhöht man das Datum um zwei Monate, so stellt man fest, dass sich die Sterne um etwa 30° entgegengesetzt zum Uhrzeigersinn gedreht haben, die Sonne aber immer noch links steht, nur über dem Horizont. Man kann nun einfach das Zeichenblatt entsprechend drehen, so dass man die Position der Sonne übertragen kann. Eine andere Variante ist, die Simulation mit einem Sternentag einfach langsam laufen zu lassen und sie drei oder viermal anzuhalten. Jetzt bleiben die Sterne stehen und die Sonne wandert im Uhrzeigersinn. g) Am Nordpol sehen wir immer denselben Himmelsteil, wir nennen ihn den nördlichen Himmel. Stehen wir am Südpol sehen wir immer den südlichen Himmelsteil. Die Sterne gehen nicht auf und nicht unter, sie drehen sich einfach in Kreisen um den Zenit, den Himmelspol, dort wo der Polarstern steht. (Nur nebenbei: Wenn wir das Datum 2000 vor Christi einstellen, so zeigt die Polachse wegen der Präzession der Erdachse nicht mehr zum Polarstern, sondern auf einen Punkt, der etwa in der Mitte zwischen der Verbindungsgeraden Alkaid (Deichselspitze des großen Wagens) und Polarstern liegt.) 3 Zusammenfassung Äquatorkoordinaten am Nordpol a) Oben haben wir den Himmel am Nordpol als Karte in unser Heft gezeichnet. Darin haben wir die Bahn der Sonne markiert. In Wirklichkeit ist der Nordhimmel aber kein Kreis, sondern eine Halbkugel. Zeichne die Skizze ins Heft und schreibe den kursiven Text ab: 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 6 Graf-Zeppelin-Gymnasium Der oben gezeichnete Himmelshalbkreis mit der Sonnenbahn ist die „Karte“ der Himmelskugel. Die Stelle, an der die Sonne am Frühlingsanfang steht, heißt Frühlingspunkt, es ist der Schnittpunkt der Ekliptikebene mit der Äquatorebene. Z.B. begann am 20.3.10 um 18:32 der Frühling Wir sehen am Nordpol immer nur Sterne oberhalb des Himmelsäquators - von dieser Halbkugel haben wir die Karte gezeichnet. Die Sonne sehen wir am Nordpol nur, wenn sie auf der Nordhalbkugel steht. Die Sonne „läuft“ nicht in der Äquatorebene, sondern in einer Ebene, die um 23,5° gegen diese Ebene geneigt ist. Diese Bahn (oder Ebene) heißt Ekliptik. Die Ekliptik ist die Projektion der scheinbaren Bahn der Sonne auf die Himmelkugel. Der Himmeläquator ist die Projektion des Erdäquators an die Himmelskugel. Ekliptik und Himmelsäquator schneiden sich im Winkel von 23,44° (= 23° 26,4’). Dies ist die Neigung der Erdachse gegen die Bahn um die Sonne. In Wirklichkeit läuft die Erde um die Sonne. Die Ebene, in der die Erde um die Sonne läuft, entspricht der Ekliptik. Die Drehachse der Erde ist um 23,5° gegen diese Erdbahn geneigt. Deshalb ist der Himmelsäquator um 23,5° gegen die Ekliptik geneigt. Wenn wir uns am Nordpol befinden, ist die Sonne oberhalb des Himmelsäquators, wenn die Erde in den linken Positionen des Bildes oben steht. Die Sonne ist dann in den Sternzeichen Widder bis Jungfrau, also in den Sternbildern Fische bis Löwe. b) 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 7 Graf-Zeppelin-Gymnasium Das folgende Bild zeigt die Erdbahn von der gegenüberliegenden Seite: c) Die Höhe der Sterne am Nordpol (und am Südpol) ändert sich nie. Wir wählen jetzt als ausgezeichnete Richtung den Strahl vom Nordpol in Richtung des Frühlingspunktes geht. Dieser Strahl geht vom Polarstern ziemlich genau in Richtung des Sternes Caph von Kassiopeia, dann weiter durch Pegasus. Am Frühlingspunkt selbst steht aber kein besonderer Stern. Wähle bei CDC den 20.3. und überprüfe die Aussage. Die Sonne steht am Horizont und die Verbindungslinie Sonne Polarstern geht durch den Stern Caph. Du kannst das Äquatoriale Koordinatensystem einschalten, klicke auf das Icon . d) Den Winkel zwischen dem Frühlingspunkt und einer anderen Stelle auf dem „Äquator“ = „Himmelsäquator“ = „Horizont am Nordpol“ nennen wir Rektaszension RA = α (right ascension). Dieser Winkel wird allerdings nicht in der Richtung der Sternbewegung 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 8 Graf-Zeppelin-Gymnasium positiv gezählt (also nach rechts, wenn wir nach Süden schauen), sondern entgegengesetzt zur Bewegungsrichtung der Sterne, also nach links. D.h. ein Stern, der die Rektaszension 315° (oder 21h, es gilt ja 1 h =15°) hat, befindet sich 45° im Uhrzeigersinn weg vom Frühlingspunkt. Die Rektaszension wird meist in Stunden (Winkelstunden) angegeben. Es gilt: 24 Stunden entsprechen 360°, bzw. 1 h = 15°. Überprüfe dies beim Stern Deneb im Schwan indem Du mit dem rechten Mauszeiger auf den Stern Deneb klickst und „Identifikation nächstes Objekt“ wählst. Die Koordinaten RA und DE stehen unterhalb der ersten Leerzeile. Aufgrund der Präzessionsbewegung der Erdachse ändern sich die Koordinaten leicht - der Frühlinspunkt wandert ja. Deshalb sind zwei Koordinaten angegeben, relativ zum gegenwärtigen Frühlingspunkt und realtiv zum Frühlingspunkt im Jahr 2000. e) Die Höhe eines Sterns am Nordpol nennen wir Deklination DE = δ (declination). Er ist der Winkel, der angibt, wie weit der Stern über dem Himmelsäquator steht. f) Diese beiden Winkel RA = α und DE = δ, die (rotierenden) Äquatorkoordinaten (Äquatorsystem, äquatoriale Koordinaten, celestial coordinates), ändern sich im Lauf unseres Lebens nicht (genauer: nur ein klein wenig aufgrund der Präzession, die ja die Position des Frühlingspunktes ändert, siehe unten bei Präzession). Damit hat jeder Stern immer gleiche Koordinaten, zumindest unabhängig von der Tageszeit und vom Beobachtungsort. g) Am Nordpol ist der Horizont mit dem Himmelsäquator identisch, der Pol steht im Zenit. Man kann den Himmeläquator mit CDC einzeichnen, wenn man auf das Icon klickt. Vom Pol aus gehen zusätzlich radiale Linien zum Äquator. Der Radius, der dicht bei Caph im Sternbild Kassiopeia vorbei geht, ist die Linie, deren Punkt alle die Rektaszension RA = α = 0h haben. Der Abstand der Linien entspricht jeweils 3h, wobei der Winkel im Uhrzeigersinn wächst (wenn man in Richtung des Polarsterns schaut. h) Kontrolliere mit CdC, dass die Sonne zum Frühlingsbeginn am Frühlingspunkt steht. Stelle dazu die entsprechende Uhrzeit (20.3.10, 18:32, bzw. eine Uhrzeit, an der laut http://de.wikipedia.org/wiki/Frühlingsbeginn. der Frühling beginnt) ein und klicke mit der rechten Maustaste auf die Sonne. Die Rektaszension RA der Sonne sollte jetzt bis auf wenige Sekunden 0h sein (oder fast 24h), ebenso die Deklination DE . Ändere jetzt die Uhrzeit um eine Stunde. Welche Koordinaten hat die Sonne jetzt? i) Während sich die Sonne in einem Jahr auf der Sonnenbahn bewegt, dreht sich die Erde etwa 366-mal um die Achse (einmal mehr als es Tage im Jahr gibt). Deshalb wandert die Sonne am Nordpol scheinbar auf einer Spiralbahn in die Höhe und wieder zurück. j) Stelle die Ekliptik, die Bahn er Sonne am Himmel dar: Klicke auf >Linien >Ekliptik. Die Sonne wandert im Lauf eines halben Jahres entgegen der Bewegungsrichtung der Sterne (das nennt man rechtläufig) nach oben und dann wieder nach unten. Im restlichen halben Jahr ist sie am Nordpol unterhalb des Horizontes. 4 Rotierende Äquatorkoordinaten an einem anderen Beobachtungsort Im Folgenden wollen wir uns eine Vorstellung der Äquatorkoordinaten an einem beliebigen Beobachtungsort auf der Erde erarbeiten. a) Wenn wir nach Süden wandern, so wandert der Pol zum Nordpunkt des Horizontes, der Himmelsäquator wird zu einem Kreis auf der Himmelskugel, der im Süden über dem Horizont liegt. Im Norden liegt er unterhalb des Horizontes. b) Wähle bei CDC die Sternwarte FN, d.h. klicke auf und dann auf 579868513 . Klicke danach auf das Icon . Beachte die Linien des Äquatorsystems. W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 9 Graf-Zeppelin-Gymnasium c) Am Äquator geht der Himmelsäquator durch den Zenit, der Nordpol steht am Horizont. Wähle die Sternwarte Äquator (Icon ) und klicke danach wieder auf die Icons und . Wir sehen am Äquator im Lauf eines Jahres alle Sterne des Himmels, ja wenn die Sterne auch tagsüber zu sehen wären, dann würden wir innerhalb von 23h 56min alle Sterne sehen. d) Unter http://astro.unl.edu/classaction/animations/coordsmotion/celestialhorizon.html findet sich ein Programm mit dem man sich den Zusammenhang Horizont = Tangentialebene veranschaulichen kann. Stelle die gewünschte Breite ein (Friedrichshafen: 47,5° Breite = Latitude) und klicke dann auf „Switch“. Wähle danach eine andere Breite, näher beim Äquator. Ein Punkt auf dem Äquator hat die Breite 0. Das ‚Ursprüngliche Bild zeigt die Himmelskugel am Nordpol. Klickt man auf Switch, so wird die Horizontebene eines Beobachters der eingegeben Breite eingeblendet und dann so gedreht, dass der Beobachter nach oben zeigt. Du kannst die Kugel mit der Maus drehen. a) Unter http://astro.unl.edu/classaction/loader.html?filename=animations/coordsmotion/celhorco mp.swf&movieid=celhorcomp&width=900&height=710&version=6.0.0 gibt es ein Programm, mit dem man sich die Äquatorkoordinaten, bzw. die Erdrotation und die Sternbewegung veranschaulichen kann Im linken Bild schaut man von außen auf die Erde, die Polachse zeigt nach Norden. Im rechten Bild steht man auf der Erde. Der Standpunkt wird unten eingegeben: FN hat die Koordinaten Latitude (Breite) Nord 47.5° und der Longitude (Länge) Ost 9,5° (drehe die linke Kugel von Hand in günstige Position) Klicke zur groben Wahl in der Weltkarte unten links auf Süddeutschland. Starte durch Klick auf den Button „start animation“ die bewegte Animation Beachte, dass sich die Erdkugel im linken Bild in die andere Richtung dreht, wie die Sterne im rechten Bild. e) Weitere Hilfe zur Veranschaulichung: http://astro.unl.edu/classaction/loader.html?filename=animations/coordsmotion/radecdem o.swf&movieid=radecdemo&width=700&height=450&version=6.0.0 (Ra, De) f) Befinden wir uns auf der geographischen Breite b, so ist der höchste Punkt des Himmelsäquators ist im Süden in der Höhe (90°-b). Der Nordpol ist auf dem Meridian (dem Großkreis N-Zenit-S) in der Höhe b, d.h. (90°-b) vom Zenit entfernt, seine Zenitdistanz ist also (90°-b). Die Sonnenbahn ist nochmals um 23,5° geneigt. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 10 Graf-Zeppelin-Gymnasium g) Notiere im Heft: (Rotierende) Äquatorkoordinaten (α/ δ) : Die Rektaszension RA = α ist der Bogenwinkel auf dem Himmeläquator vom Frühlingspunkt in Richtung von Süd nach Ost, also nach links (wenn man nach Süden schaut). Die Rektaszension der Sonne vergrößert sich von Tag zu Tag um etwa 1° = 1/15h – die Sonne bleibt relativ zu den Sternen jeden Tag um etwa 1°= 4 min zurück. Zum Frühlingsanfang ist die Rektaszension der Sonne 0° = 0h. Zu Beginn des Sommers ist die Rektaszension der Sonne ungefähr 90° = 6h. Die Deklination DE = δ ist die Höhe des Sterns über der Äquatorlinie. Zeichne bitte folgende Abbildung in Dein Heft: h) Im Internet gibt es Programme, mit denen man sich die Äquatorkoordinaten veranschaulichen kann: http://astro.unl.edu/classaction/loader.html?filename=animations/coordsmotion/radecdem o.swf&movieid=radecdemo&width=700&height=450&version=6.0.0 Nutze dies aus, spiele ein wenig mit dem Applet auf dieser Seite. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 11 Graf-Zeppelin-Gymnasium 5 Feststehende Äquatorkoordinaten b) Unter dem Stundenwinkel t eines Sterns versteht man den Winkel auf dem Äquator zwischen dem Süden und Stundenkreis eines Sterns. Lese bitte http://de.wikipedia.org/wiki/Stundenwinkel . Zeichne bitte folgende Abbildung in Dein Heft: c) Im Folgenden benötigen wir vor allem den Stundenwinkel des Frühlingspunktes, der Sternzeit θ genannt wird, siehe unten. Notiere im Heft: Die Bezugsebene des ruhenden Äquatorialen Koordinatensystem (t / δ) = (Stundenwinkel / Deklination) ist wieder die Äquatorebene, nur dass die Koordinate auf dem Äquator nicht vom Frühlingspunkt, sondern vom Süden des Beobachters aus gemessen wird, allerdings nicht nach links, sondern nach rechts. Damit ändert sich der Stundenwinkel im Prinzip so wie der Azimut. 6 Sternzeit a) Der Stundenwinkel eines Sterns wächst mit der Rotation der Erde ständig. Er gibt uns an, wie viel Zeit seit der Kulmination eines Gestirns vergangen ist. Ein Stern kulminiert, wenn er im Süden, wenn er auf dem Meridian steht. Die Sternzeit gibt an, wie weit sich der Frühlingspunkt von seiner Kulmination aus nach Westen bewegt hat, d.h. die Sternzeit ist der Stundenwinkel des Frühlingspunktes. Ein Stern, der um den Winkel α links vom Frühlingspunkt steht, der also die Rektaszension α hat, steht zur Sternzeit θ um α weniger weit rechts als der Frühlingspunkt. Sein Stundenwinkel ist also um α kleiner also der Stundenwinkel des Frühlingspunktes = die Sternzeit θ Notiere und merke dir: Die Sternzeit ist der Stundenwinkel des Frühlingspunktes. Für den Stundenwinkel t eines beliebigen Sterns gilt Stundenwinkel = Sternzeit – Rektaszension kurz t=θ–α b) Im Internet gibt es ein Progrämmchen, mit dem man sich den gerade abgeleiteten Zusammenhang veranschaulichen kann. Es gilt: sidereal time = Sternzeit 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 12 Graf-Zeppelin-Gymnasium hour angle = Stundenwinkel latitude = Breite der Erde right ascension = Rektaszension declination = Deklination c) Wir überprüfen die Gleichung von a) mit Hilfe von CdC (auf den Stern mit der rechten Maustaste klicken und Identifikation nächstes Objekt wählen): i) Sonne am 23.3.09 um 12:44 (Die Sonne steht im Frühlingspunkt!) Der Stundenwinkel: t = …. (CDC, Genauigkeit in min) Die Sternzeit: Sz = ….(CDC, Genauigkeit in min) Die Rektaszension: α = … (CDC, Genauigkeit in min) Test: Sternzeit - Rektaszension ii) Caph Rechtes Ende des Kassiopeia-Sternbilds Der Stundenwinkel: t = …. (CDC, Genauigkeit in min) Die Sternzeit: Sz = ….(CDC, Genauigkeit in min) Die Rektaszension: α = … (CDC, Genauigkeit in min) Test: Sternzeit - Rektaszension iii) Beteigeuze im Orion Der Stundenwinkel: t = …. (CDC, Genauigkeit in min) Die Sternzeit: Sz = ….(CDC, Genauigkeit in min) Die Rektaszension: α = … (CDC, Genauigkeit in min) Test: Sternzeit – Rektaszension (Lösungen siehe Astro_Koordinaten.ppt) d) Da zur Bestimmung der Rektaszension eines Sterns der Frühlingspunkt benötigt wird, müssen wir ihn am Himmel finden können. Dies geht mit dem Sternzeitzeiger. Die Sternzeit θ eines Ortes (die man mit Hilfe des Sternzeitzeigers am Himmel ablesen kann) bestimmt die Position des Frühlingspunktes. (Am Nordpol ist die Sternzeit der Azimut a des Frühlingspunktes, da dort der Himmelsäquator und der Horizont zusammenfallen (bei CdC gilt Az=a+180°) e) Verbinde auf Deiner Skizze von 1i) oben den Polarstern mit Caph in der Kassiopeia und verlängere ihn. Diese Linie zeigt ziemlich genau zum Frühlingspunkt. Diese Strecke heißt Sternzeitzeiger (Sternstundenzeiger, Himmelszeiger, Himmelsuhrzeiger oder Ähnliches – allerdings sind die Namen nicht festgelegt, ich weiß auch nicht, welche sich durchsetzen.) f) Notiere im Heft und zeichne die folgende Skizze ab: Wenn wir den Polarstern in Gedanken mit Caph in Kassiopeia verbinden und verlängern, kommen wir zu α And, d.h. zum linken oberen Eck des Pegasusquadrats, und dann weiter zum Frühlingspunkt. Am Nordpol liegt der Frühlingspunkt am Horizont. An den anderen Orten ist auf dem Himmelsäquator. Es ist einer der beiden Schnittpunkte des Himmelsäquators mit der Ekliptik. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 13 Graf-Zeppelin-Gymnasium g) Dieser Sternzeitzeiger dreht sich mit den Sternen innerhalb von 23h 56 min einmal um den Polarstern. Wenn der Frühlingspunkt im Süden steht, dann zeigt der Sternzeitzeiger, wenn wir nach Norden blicken, nach oben. Eine viertel Erdumdrehung später zeigt der Sternzeitzeiger waagrecht nach links (nach Westen), er hat sich also um 90° entgegen dem Uhrzeigersinn gedreht. Der Frühlingspunkt liegt also im Westen, siehe auch 1d). h) Wir veranschaulichen uns dies sowohl am Nordpol als auch in Friedrichshafen. Wer möchte kann dies auch noch am Äquator und am Südpol tun (in allen Positionen ist die geographische Länge mit der in FN identisch, wenn wir in CdC die entsprechende Sternwarte wählen) i. Gehe in CdC zum Nordpol und wähle 20.3.2010, 12:30:56. Blicke nach Süden. Die Sonne steht jetzt im Süden am Horizont. Die Sternzeit ist damit θ = 0° = 0h. Der Sternzeitzeiger zeigt nach oben, wenn wir nach Norden blicken. ii. Animiere mit der Schrittweite von etwa 2 min. blicken wir nach Norden, so wandert der Sternzeitzeiger langsam nach links, er dreht sich also im Gegenuhrzeigersinn um den Polarstern. iii. Am 20.3.2010 um 18:29:55 steht der Frühlingspunkt im Westen, es ist also 6 iv. Wiederhole die obigen drei Punkte bei der Sternwarte Friedrichshafen. i) Notiere im Heft: Mit Hilfe des Sternzeitzeigers können wir also die Position des Frühlingspunktes bestimmen und die Sternzeit näherungsweise erkennen. Seine Position ist die Sternzeit θ. Blicken wir nach Norden, so stellen wir fest, dass sich der Sternzeitzeiger einmal in 23h 56 min einmal um den Polarstern dreht. Zeigt der Zeiger nach oben, so ist es 0 Uhr Sternzeit, der Frühlingspunkt steht im Norden. Der Zeiger dreht sich mit den Sternen, wenn wir nach Norden zeigen also in mathematisch positivem Sinn, also entgegen dem Uhrzeigersinn. Wenn er eine viertel Umdrehung gemacht hat, dann ist die Sternzeit 6 Uhr, d.h. der Frühlingspunkt liegt im Westen. Nach 11 Stunden und 58 min zeigt er zum Horizont, es ist also 12 Uhr Sternzeit, der Frühlingspunkt ist dann genau im Norden 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 14 Graf-Zeppelin-Gymnasium j) Die Faustformel für die Sternzeit bei uns lautet: Sternzeit = Uhrzeit in MEZ plus (MONAT * 2 + 4) Stunden plus (TAG * 4 + 20) Minuten z.B. 20.6.08 9:30: Schätzwert für θ = 9:30 + (6*2+4) h + (20*4+20) min = 9:30 +16h + 100 min = 25h:130min = 3:10. Trage diesen Wert unter SZ Formel ein. k) Aufgabe: Übertrage die folgende Tabelle ins Heft und fülle sie wie folgt aus (Die Zeiten sind alle in MEZ = UT+1, nicht in MESZ!, da CdC so eingestellt ist) 1) Schaue in CdC nach Norden und lese mit Hilfe des Sternzeitzeigers (= PolarsternCaph-Zeigers), dem Zeiger zum Frühlingspunkt, näherungsweise an den unten angegebenen Zeiten die Sternzeit θ ab. Trage diesen Wert unter „Schätzung SZ“ ein. 2) In der Spalte „SZ Formel“ trägst Du bitte das Ergebnis der Faustformel ein, die im nächsten Punkt, d.h. in j) (siehe auch Astro_Koordinaten.ppt, Folie 29) erklärt wird. 3) In der dritten Spalte „SZ CdC“ tragen wir den (wirklichen) Wert ein, den wir folgendermaßen erhalten: In CdC klickst Du mit der der rechten Maustaste auf einen Stern und wählst „Identifikation nächstes Objekt“. Dort findest Du die Sternzeit. Datum Schätzung SZ SZ Formel 20.6.09 9:30 1.3.09 22:00 16.3.09 22:00 10.9.09 22:30 (Lösungen siehe Astro_Koordinaten.ppt) SZ CdC l) Wem diese Faustformel nicht genau genug ist, der kann in Wikipedia unter Sternzeit eine genaue Formel nachlesen (und anwenden). Unter http://www.astronomia.de/index.htm?http://www.astronomia.de/zeit.htm oder http://www.schulmodell.de/astronomie/chemnitz/rechner.php findet man ein OnlineProgramm zum Berechnen der Sternzeit.(die Breite von FN ist 9,48°) Weitere Infos: siehe http://www.praxelius.de/astro/sternz.htm oder http://www.sternenhimmel.info/sternzeit.html 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 15 Graf-Zeppelin-Gymnasium 7 Einen Stern mit Hilfe der Koordinaten RA und DE finden. Übung: Wähle das Datum 15.12.12 und die Uhrzeit 23:00 Wir suchen den Stern mit den Koordinaten RA = 10h08 und DE = 11°58’. Wo finden wir ihn am Himmel von Fn am 15.12,12 um 23 Uhr? Vorgehen: a) Besorge Dir die Sternzeit von FN am 15.12.12 um 23:00 Erinnerung: Die Sternzeit ist der Stundenwinkel des Frühlingspunktes. Die findest ihn entweder mit Hilfe des Frühlingspunktes oder mit der Näherungsformel Sternzeit = MEZ + (MONAT mal 2 plus 4) Stunden plus (TAG mal 4 plus 20) Minuten Variante 1: Die Sternzeit kannst Du damit bestimmen, dass Du nach Norden schaust, den großen Wagen suchst, zum Polarstern gehst und dann den Zeiger Polarstern-Caph betrachtest. Er bewegt sich in 24 Sternstunden (= 23 Sonnenstunden und 56 min) einmal um den Polarstern. Steht er oben ist es 0 Uhr Sternzeit, steht er unten, ist es 12 Uhr Sternzeit, links: 6 Uhr, rechts: 18 Uhr. 30° sind 2 Stunden, 45° drei Stunden. Hier gilt: Sternzeit etwa 4 Uhr Variante 2: Faustformel: Sternzeit = Uhrzeit in MEZ plus (MONAT * 2 plus 4) Stunden plus (TAG * 4 plus 20) Minuten (siehe oben 6j) Hier also: 23h+0min + (12*2+4) h + (15*4+20) min = 23h+28h + 0 min + 80 min = 4h 20 min = 4h20min Variante 3. Wir können die Sternzeit auch bei CDC ablesen: 4h18m (rM auf beliebigen Stern >Identifikation nächstes Objekt >im 3. Abschnitt unter Fn steht die Sternzeit) Variante 4: Starte in PoProgs\Astro\AstroTools das Excel-File AstroDaten_FN.xls und gib in den Zeilen 13 und 14 das Datum und die Uhrzeit ein, so findest Du in Zeile 21 die Sternzeit von FN, hier 4:17:48 b) Stundenwinkel berechnen: Wenn es so viel Uhr Sternzeit ist, wie die RA sagt (d.h. hier um 10h08 Sternzeit), steht der Stern im Zenit. Bis dahin fehlen noch etwa 6 Stunden. Damit ist der Stern 6 Stunden vor der Kulmination. Wenn wir nach Süden blicken ist er also etwa 90° links von der Blickrichtung, also ziemlich genau im Osten. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 16 Graf-Zeppelin-Gymnasium Wer möchte kann auch sagen: Der Stundenwinkel ist t = Sternzeit – RA = 4:12 -10:08 = -6:04. (Merke: Der Stundenwinkel zählt nach rechts positiv!) c) Die Deklination des Sterns De=11,58° gibt an, wie viel Grad er oberhalb des Himmelsäquator ist. Der Himmeläquator ist im Osten und Westen am Horizont, im Süden in der Höhe 90°-Breite FN = 90°-47,5° = 42,5°. Hier steht der Stern also etwa 12 ° über dem Himmelsäquator im Osten. Da es von der Ebene des Himmelsäquator aus senkrecht nach oben geht, d.h. also leicht nach links an dieser Stelle, ist er links von Osten zu finden. d) Kontrolle: Blicke also nach Osten. Stelle den FOV (mit der Stern etwas links von der Mitte zu finden sein. Skala) auf 24°. Dann sollte e) Die genauen Werte der lokalen Horizontkoordinaten, erhältst du bei CDC: Azimut Az = 83°35’, d.h. a=180-Az = 96°25’ // Höhe h = 10°24’ (siehe auch nächsten Abschnitt) 8 Sternzeit und Umrechnungen der Koordinaten In diesem Teil wollen wir uns überlegen, wie man aus den Äquatorkoordinaten, dem Beobachtungsort und der Beobachtungszeit, genauer der Sternzeit, den Azimut und die Höhe eines Sterns berechnen kann. d) Am Nordpol gilt: Der Himmelsäquator ist hier mit dem Horizont identisch. Wenn wir die Sternzeit θ, den Azimut des Frühlingspunktes am Nordpol kennen, kennen wir auch den Azimut a des Sterns am Nordpol: a = θ – α = Sternzeit – RA i. Beispiel: Gehe mit CdC an den Nordpol. Wähle die Uhrzeit 20.3.2010, 19:29:55. Blicke nach Süden. Dies Sonne steht jetzt im Westen am Horizont (also rechts). Die Sternzeit ist damit θ = 90° = 6h. ii. Wenn wir nun in CdC mit der rechten Maustaste auf den hellen Atair rechts oben klicken und „Identifikation nächstes Objekt“ wählen, finden wir: Sternzeit 6h:00. Die Rektaszension RA ist 19h:51. Damit ist der Azimut a = 6:00h – 19:51h = – 51 360 207,5 152,5 . Da der Azimut 13h:51 = 10h:09 oder a 13 h 60 24h in CdC von Norden, statt von Süden aus gerechnet wird, finden wir dort bei CDC AZ = 152,5°+180° = 332,5° e) Das was am Nordpol der Azimut ist, ist an anderen Orten der Winkel, den der Frühlingspunkt auf dem Himmelsäquator mit dem Süden des Äquators bildet. Dieser Winkel heißt Stundenwinkel t des Stern. f) Wenn wir helle Sterne am Himmel suchen, müssen wir normalerweise die Äquatorkoordinaten nicht umrechnen. Wir können dann einfach mit dem Sternzeitzeiger den Frühlingspunkt suchen, den Äquator abschätzen (etwa Kopf Richtung Polarstern, Arme ausbreiten, die Ebene die sie bilden, ist der Äquator) und vom Frühlings aus die Rektaszension nach links gehen, die Deklination nach oben. Dort steht der Stern dann. g) Wenn man die Sterne mit einem Teleskop in Deutscher Montierung betrachtet (siehe etwa AB_Teleskopfuehrerschein.doc), so zeigt die Achse der Montierung in Richtung des Pols, die Drehrichtung des Tubus ist mit der Äquatorebene identisch. Man braucht also nur die Sternzeit, die Stellung des Frühlingspunktes, den man mit dem Sternzeitzeiger findet, um dann durch Drehen des Tubus und Nicken den Stern zu finden. Allerdings müssen wir beachten, dass der Frühlingspunkt sich nach rechts wegdreht – und damit natürlich die Sterne ebenfalls, d.h. ein Fernrohr, das eine stärkere Vergrößerung hat, also 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 17 Graf-Zeppelin-Gymnasium nur einen kleinen Himmelsausschnitt zeigt, muss regelmäßig nachbewegt werden, aber das lernen wir beim Teleskopführerschein. h) Wir können aber (wenn auch mit etwas Aufwand, mit dem Taschenrechner, mit sin und cos) die rotierenden Äquatorkoordinaten (α, δ) in zwei Schritten in die Horizontkoordinaten (a, h) umrechnen: Mit Hilfe der Sternzeit, wandeln wir die die Koordinaten (α, δ) in die ruhenden Äquatorkoordinaten (t / δ) um. und dann diese in die Horizontkoordinaten i) Schritt 1: Wandle (α, δ) = (Ra/De) in (t / δ) um. Dies ist einfach, wenn Du die Sternzeit kennst (siehe oben): t = θ – α = Sternzeit – RA j) Schritt 2: Dieser Schritt ist mathematisch etwas anspruchsvoller: sh sin(h) sin(Breite) sin(De) cos(Breite) cos(De) cos(t) cos(De) sin(t) sa sin(a) cos(h) Da h zwischen -90° Und 90° ist, ist h=asin(h) eindeutig. a kann alle Werte zwischen -180° und 180° annehmen. Also gibt es zwei mögliche Lösungen: a1=asin(sa) und a2=180-a1 – je nachdem, ob der Stern in der südlichen oder nördlichen Hälfte des Himmels ist. (siehe http://de.wikipedia.org/wiki/Nautisches_Dreieck oder http://www.greiergreiner.at/hc/sph_dreieck.htm ) Anmerkung zu Schritt 2: Neugierige, die genauer wissen wollen, wie man zum Sternzeitpunkt θ die Sternkoordinaten (α / δ) = (Rektaszension / Deklination) in die Horizontkoordinaten (a,h) umrechnet, finden bei http://www.greiergreiner.at/hc/sph_dreieck.htm die nötigen (nicht ganz einfachen) Infos. Weitere Infos und Ableitungen siehe: http://de.wikibooks.org/wiki/Astronomische_Berechnungen_f%C3%BCr_Amateu re/_Positionsastronomie/_Koordinatentransformationen, hier finden sich auch Beispiele. Eine generelle Einführung in die sphärische Trigonometrie findet man unter dem Link http://andreas.forstner-burgau.de/Facharbeit.pdf oder wenn man eine relative praktische Einführung sucht: http://www.ottmarlabonde.de/L1/Astr05.html und die folgenden (und evtl. vorigen) Seiten. k) Wer will kann die Koordinaten damit direkt mit dem GTR (oder mit SpeedCrunch) berechnen: Allerdings ist dies nicht ganz einfach. Mit Ra =10h09 und De = 11°54’ uns der Sternzeit Sz = θ = 4:18 ergibt sich De = δ = Deklination, hier 11:54 = 11+54/60 = 11,9° Sz = θ hier 4:18 = (4+18/60)*15° = 64,5° t = Sz – Ra = Stundenwinkel, hier 64,5°-(10+9/60)*15°= -87,75° Breite von FN = 47,5° Es ergibt sich mit den beiden Gleichungen oben (GTR auf DEG stellen) sh = 0,1780 oder Höhe h = asin(..) = 10,25°= 9° und 0,25*60min = 10:15 sa = -0,9936 oder Azimut a1 = asin(..) = -83,52 oder a2=180-a1=263,5 =360-263.5 = 96,5. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 18 Graf-Zeppelin-Gymnasium 9 Analemma a) Gehe bei CdC zur Sternwarte FN und schaue nach Süden. Stelle das azimutale Koordinatensystem ein, das Horizontsystem. Wähle den 20.3.2010 und bestimme die Uhrzeit des Sonnenhöchststandes. Schalte das Äquatoriale Koordinatengitter ein (>Linie >Äqu…) und animiere mit 1 Tag. Die Sterne drehen sich nun gegen den Uhrzeigersinn. Die Sonne aber bleibt fast stehen, sie bewegt sich rauf und runter. b) Im Frühling steht die Sonne auf dem Himmeläquator, im Frühlingspunkt. Notiere im Heft, wie man den Frühlingspunkt definiert (siehe oben). Wie hoch steht die Sonne, wenn der Beobachtungsort die geographische Breite b hat (siehe oben, etwa 2f)? Wie hoch steht die Sonne also in FN zum Frühlings- und zum Herbstanfang? Notiere dies im Heft. (Die Breite von FN ist 47,5°) c) Im Sommer steht d) Notiere in Deinem Heft, was Du über die Bewegung der Sonne sagen kannst. Die Bahn auf der sich die Sonne bewegt, heißt Analemma. Recherchiere im Internet (evtl. bei Wikipedia) hierzu, siehe auch http://www.perseus.gr/Astro-Solar-Analemma.htm Skizziere diese Analemmakurve im Heft. Notiere, warum die Analemmabewegung der Sonne im Altertum unbekannt war(siehe Wikipedia). e) Merke: Blicken wir an irgendeiner Stelle auf der Nordhalbkugel immer zum Polarstern, so dreht sich der Himmel um diese Stelle. Dies nutzen wir bei der Sternbeobachtung mit der deutschen Montierung aus. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 19 Graf-Zeppelin-Gymnasium 10 Präzession der Erde a) Notiere im Heft: Alle Sterne haben in dem rotierenden Äquatorialen Koordinatensystem (α / δ) = (Rektaszension / Deklination) Koordinaten, die sich im Lauf eines Menschenlebens nur unmerklich ändern. Merke aber: Diese Koordinaten ändern sich im Lauf der Jahrzehnte leicht, da sich aufgrund der Präzession der Erde sowohl der Himmelsäquator als auch der Frühlingspunkt verschieben. Die Erdachse zeigt nur alle 25 700 Jahre auf den Polarstern.) b) Die Präzession bewirkt, dass der Frühlingspunkt jedes Jahr etwas der Sonnenbewegung entgegen wandert. Dadurch ist die Zeit, die die Sonne benötigt, um wieder an den Frühlingspunkt zu kommen gut 20 min (und 23s) kürzer als die Zeit für einen Umlauf. c) Notiere im Heft: Die Zeit für einen Umlauf heißt siderisches Jahr, die Zeit, die die Sonne benötigt, um an den Frühlingspunkt zurück zu kommen heißt tropische Jahr. Dauer des siderischen Jahres: 365, 256 Tage (genauer: 31558149,54 Sekunden oder 365 Sonnentagen, 6 Stunden, 9 Minuten und 9,54 Sekunden oder 366 siderischen Tagen, 6 Stunden, 9 Minuten und 9,78 Sekunden. (siehe http://de.wikipedia.org/wiki/Siderisches_Jahr) Dauer des tropischen Jahres: 365,2422 Tage (genauer 365,24219052 Tage = 365 Tage, 5 Stunden, 48 Minuten, 45,261 Sekunden, siehe http://de.wikipedia.org/wiki/Tropisches_Jahr ) Ein Tag gesteht dabei aus 24*3600=86400 Sekunden, wobei die Sekunde die Zeiteinheit im SI-Einheitensystem ist. d) Die Ursache der Präzession der Äquatorwulst, den die Erde aufgrund ihrer Rotation bekommt. Die Sonne übt nun ein Drehmoment auf die Erde aus, was zur Folge hat, dass die Drehachse im Raum rotiert. Die Neigung der Drehachse gegen die Eklipse ist dabei konstant 23,5°. Der Präzessionskegel hat also einen Öffnungswinkel von 47°. Das hat zur Folge, dass der Frühlingspunkt innerhalb von 25 800 Jahren einmal um die Sonne wandert. Dadurch ändern sich die Äquatorkoordinaten pro Jahr um 0,014°=50,4’’. Bereits Hipparchos hat diesen Effekt vor 2000 Jahren beschrieben. Wahrscheinlich haben die Babylonier diesen Effekt bereits 170 Jahre früher festgestellt. e) In den letzten 2100 Jahren ist der Frühlingspunkt dadurch um 23 2100 20 min 713, 4h 29, 71d nach vorne gewandert. So dass die inzwischen 60 rund einen Monat „zu spät“ in den Sternbildern steht. Damit hinkt die Sonne den Sternzeichen um rund einen Monat hinterher. 579868513 W.Seyboldt Stand: 31.1.2 Arbeitsblatt Koordinatensysteme - Astronomie Seite 20 Graf-Zeppelin-Gymnasium i Merke (Hefteintrag) Die Sterne wandern im Gegenuhrzeigersinn um den Polarstern. Sie gehen nicht auf und nicht unter. Für eine Umdrehung benötigen sie 23 h und 56 min. Dasselbe gilt näherungsweise für die Sonne. Sie steht 24 Stunden lang am Himmel. Wenn man allerdings genauer hinschaut oder mehrer Tage beobachtet, erkennt man, dass sie jeden Tag etwa ein Grad im Vergleich zu den Sternen zurückbleibt und langsam an Höhe gewinnt, bis es Sommer ist. Dann verliert sie wieder an Höhe. ii Merke (Hefteintrag) Wenn wir in Richtung des Polarstern, des Himmelsnordpols schauen, so drehen sich die Sterne umgekehrt wie die Uhr, also mathematisch positiv. iii Merke (Hefteintrag) Die Sterne stehen nun scheinbar fest. Die Sonne wandert nun im Uhrzeigersinn um den Polarstern. Ebenso der Mond und die Planeten (allerdings wandern diese mitunter auch in die andere Richtung). Die sonnennahen Planeten wandern schnell, die sonnenfernen langsam. Die Sonne schraubt sich hoch und wieder herunter. Sie ist ein halbes Jahr am Himmel zu sehen (im Frühling und im Sommer), dann ist sie untergegangen (im Herbst und im Winter). iv Merke (Hefteintrag) Der Mittelpunkt der Sonne geht etwa am 20. oder 21.3. auf und am 22. oder 23.9. unter. 579868513 W.Seyboldt Stand: 31.1.2