Das Zählprinzip

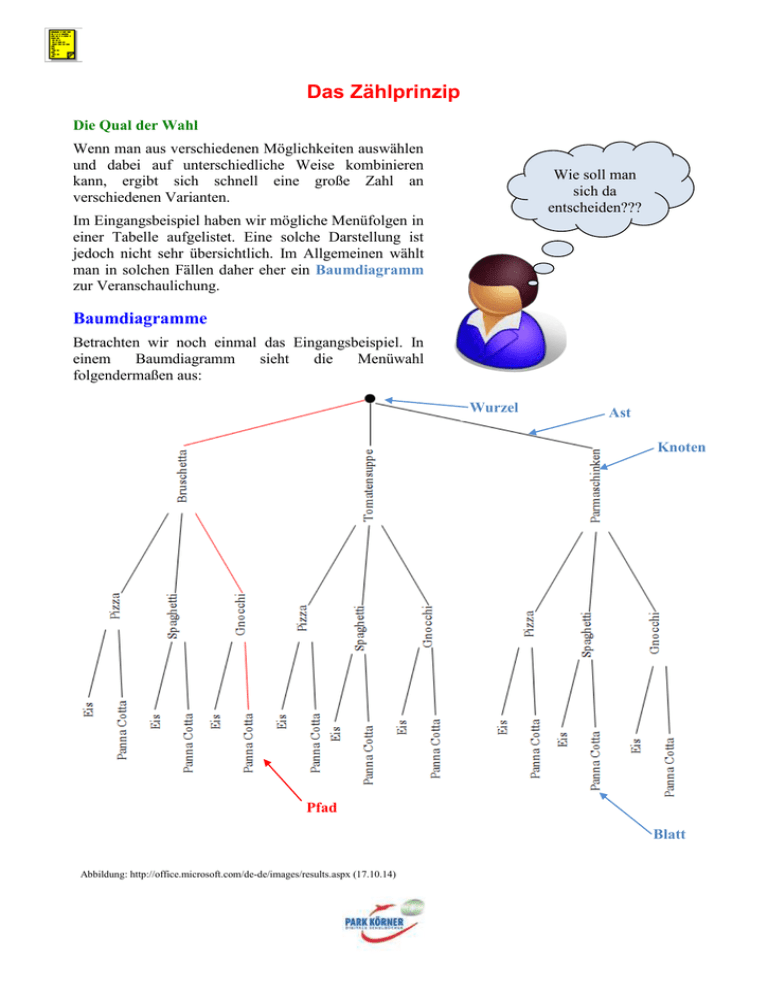
Das Zählprinzip
Die Qual der Wahl
Wenn man aus verschiedenen Möglichkeiten auswählen
und dabei auf unterschiedliche Weise kombinieren
kann, ergibt sich schnell eine große Zahl an
verschiedenen Varianten.
Wie soll man
sich da
entscheiden???
Im Eingangsbeispiel haben wir mögliche Menüfolgen in
einer Tabelle aufgelistet. Eine solche Darstellung ist
jedoch nicht sehr übersichtlich. Im Allgemeinen wählt
man in solchen Fällen daher eher ein Baumdiagramm
zur Veranschaulichung.
Baumdiagramme
Betrachten wir noch einmal das Eingangsbeispiel. In
einem
Baumdiagramm
sieht
die
Menüwahl
folgendermaßen aus:
Wurzel
Ast
Knoten
Pfad
Blatt
Abbildung: http://office.microsoft.com/de-de/images/results.aspx (17.10.14)
Jedes Baumdiagramm besteht aus den folgenden Bestandteilen:
Knoten: die Verzweigungspunkte des Baums
Wurzel: der Startknoten des Baums
Ast: die Verbindung zwischen zwei Knoten
Blatt: Endknoten des Baums
An jedem Knoten muss eine Entscheidung getroffen werden, welcher Ast gewählt wird. Ein Weg
von der Wurzel bis zum Blatt wird Pfad genannt. Jeder Pfad stellt eine Auswahlmöglichkeit dar, im
obigen Beispiel also eine mögliche Menüfolge. Die Anzahl der Blätter eines Baums zeigt die Zahl
der Wahlmöglichkeiten.
Zählprinzip
Für das Beispiel ergaben sich 18 verschiedene mögliche Menüfolgen. Rechnerisch ergibt sich die
Anzahl an möglichen Zusammenstellungen als Produkt aus der Zahl der Wahlmöglichkeiten auf
jeder Stufe des Baums.
Merke:
Hat man auf der ersten Stufe n1 Wahlmöglichkeiten, auf der zweiten Stufe n2 Wahlmöglichkeiten,
auf der dritten Stufe n3 Wahlmöglichkeiten, ..., dann ist die Gesamtzahl der Wahlmöglichkeiten
gleich n1 ∙ n2 ∙ n3 ... Das nennt man auch das Zählprinzip.
Im Beispiel:
3 Vorspeisen
3
3 Hauptspeisen
∙
3
2 Desserts
∙
2
= 18
Eingeschränkte Wahlmöglichkeiten
Das bisherige Beispiel geht davon aus, dass die Auswahl aus den Vorspeisen, Hauptspeisen und
Desserts völlig unabhängig voneinander erfolgt.
Marie findet jedoch, dass bestimmte Menüfolgen überhaupt nicht passen. Bruschetta und Pizza
passen zum Beispiel nicht in ein Essen, denn beides ist doch letztlich ein Teig mit Belag. Das ist zu
wenig Abwechslung. Auch Tomatensuppe und Spaghetti Bolognese passen nicht zusammen, das
sind zu viele Tomaten auf einmal! Und Parmaschinken mit Melone mag sie ohnehin nicht.
Wie viele Wahlmöglichkeiten hat also Marie in diesem Szenario?
Betrachten wir den zugehörigen Baum, dann ergeben sich nun folgende Wahlmöglichkeiten:
Marie hat damit 2 ∙ 2 ∙ 2 = 8 Wahlmöglichkeiten.
Beachte:
Wenn man die Anzahl der Wahlmöglichkeiten feststellen möchte, muss man immer überlegen, ob
eine Auswahl auf einer Stufe Einfluss auf die Wahlmöglichkeiten der nächsten Stufe hat.
Fakultät
Betrachten wir noch ein anderes Beispiel:
Ina hat 5 Spielsteine mit den Nummern 1 – 5:
1
2
3
4
5
Wie viele fünfstellige Zahlen kann sie daraus bilden?
Schauen wir uns an, welche Auswahl Ina jeweils hat.
Beim ersten Mal kann sie aus 5 Spielsteinen wählen. Sie hat also 5 Möglichkeiten für die erste
Ziffer der neuen Zahl. Für die zweite Ziffer kann sie aber nur noch aus 4 Steinen wählen (ein Stein
wurde ja bereits verwendet und steht nicht mehr zur Verfügung). Für die dritte Ziffer hat sie
folglich noch eine Auswahl aus 3 Steinen, für die vierte Ziffer aus zwei Steinen und für die letzte
Ziffer bleibt dann nur noch ein Stein übrig.
Ina hat also 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 120 Möglichkeiten, eine Zahl zu bilden.
Das Produkt 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 schreibt man auch als 5! (sprich „5 Fakultät“).
Merke:
Die Fakultät einer Zahl n, geschrieben n!, bezeichnet das Produkt aller natürlichen Zahlen kleiner
oder gleich n.
Beispiele:
1! = 1
2! = 2 ∙ 1
3! = 3 ∙ 2 ∙ 1
usw.