Zu Blatt 1:

Formelsammlung
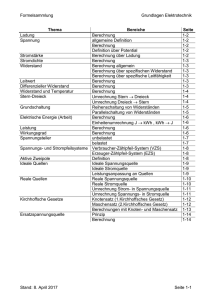
Thema
Komplexe Zahlen
Bedienungsanleitung für TR
Rechnen mit komplexen Zahlen
Grundzweipole komplex dargestellt
Komplexe Widerstände
Komplexe Leistung
Grundschaltungen komplex
Resonanz
Dämpfung
Komplexe Übertragungsfunktion
Frequenznormierung (Bode-Diagr.)
Stand: 8. April 2017
Elektrotechnik
Bereiche
Definition
Normalform
trigonometrische Form
Eulersche Form
Versorform
Sharp EL546R
Casio fx-991WA
Gleichheit von komplexen Zahlen
Konjugiert komplexe Zahlen
Addition und Subtraktion
Multiplikation und Division
Definition von j
Multiplikation komplex mit konjugiert komplex
Inversion einer komplexen Zahl
Widerstand komplex
Spule komplex
Kondensator komplex
Zeigerdiagramm
Berechnung
Zeigerdiagramm
Berechnung
Reihenschaltung komplexer Widerstände
Parallelschaltung komplexer Widerstände
Umwandlung Reihen- in Parallelschaltung
Umwandlung Parallel- in Reihenschaltung
Definition
Reihenresonanz
Parallelresonanz
Definition
Dämpfungsmaß
Übertragungsfunktion allgemein
Amplituden-Frequenzgang allgemein
Phase-Frequenzgang allgemein
RC-Tiefpaß
RC-Hochpaß
RL-Tiefpaß
RL-Hochpaß
Definition und Normierung
Normierter Tiefpaß
Normierter Hochpaß
Bode-Diagramme Tiefpaß
Bode-Diagramme Hochpaß
Seite
4-2
4-2
4-2
4-2
4-2
4-3
4-3
4-4
4-4
4-4
4-5
4-5
4-5
4-5
4-6
4-6
4-6
4-7
4-7
4-7
4-7
4-8
4-8
4-8
4-9
4-9
4-9
4-10
4-11
4-11
4-12
4-12
4-12
4-13
4-14
4-15
4-16
4-17
4-17
4-17
4-18
4-19
Seite 4-1
Formelsammlung
Elektrotechnik
Komplexe Zahlen und deren Darstellung:
c  a  j b
c = c komplex
a = Realanteil von c ( auch Re {c} )
b = Imaginäranteil von c ( auch Im {c} )
Darstellungsformen:
1. Normalform (algebraische Schreibweise):
c  a  j b
2. Polarform ( trigonometrische Schreibweise ):
c  a 2  b2
|c| = Betrag (Länge) von c komplex
c  c  cos  j  sin  
a  c  cos
b  c  sin 
3. Eulersche Form ( Exponentialschreibweise ):
Nach Euler gilt: e j  cos  j  sin 
 c  c  e j
4. Versorform:
c  c 
(  sprich: versor phi )
Stand: 8. April 2017
Seite 4-2
Formelsammlung
Elektrotechnik
Umrechnung komplexer Zahlen mit dem Taschenrechner:
Taschenrechner Sharp EL546R:
Mit 2ndF + Math + 1 den Taschenrechner in den Modus für komplexe Zahlen bringen.
Mit Math + 1 wird die Darstellung in der Versorform eingestellt. (r0-Anzeige im Display)
Mit Math + 2 wird die Darstellung in der Normalform eingestellt. (xy-Anzeige im Display)
Mit 2ndF + Exp wird zwischen der Anzeige des Realanteils und des Imaginäranteils von c
bzw. zwischen der Anzeige des Betrages und  von c hin und her gewechselt.
Mit ab/c wird das j-Zeichen dargestellt. Mit D°M’S wird das Versor-Zeichen dargestellt.
Umrechnung Normalform  Versorform:
- Taschenrechner auf Versorform einstellen ( Math + 1 )
- Komplexe Zahl in der Normalform eingeben und mit = betätigen (z.B. 3 + ab/c 2 = )
- Es wird der Betrag von c angezeigt
- Für  2ndF + Exp betätigen
Umrechnung Versorform  Normalform:
- Taschenrechner auf Normalform einstellen ( Math + 1 )
- Komplexe Zahl in der Versorform eingeben und mit = betätigen (z.B. 3 D°M’S 2 2 = )
- Es wird der Realanteil von c angezeigt
- Für den Imaginäranteil 2ndF + Exp betätigen
Taschenrechner Casio fx 991 WA:
Mit Mode + 2 den Taschenrechner in den Modus für komplexe Zahlen bringen.
!!! Die Darstellung erfolgt immer in der Normalform !!! Keine Umstellung auf die
Versorform im komplexen Modus möglich.
Mit ENG wird das j-Zeichen dargestellt.
Betrag einer komplexen Zahl (z.B. 3 + j4) berechnen:
Shift ) ( 3 + 4 ENG ) = eingeben.
Winkel einer komplexen Zahl (z.B. 3 + j4) berechnen:
Shift ( ( 3 + 4 ENG ) = eingeben.
Umrechnungen zwischen der Versorform und der Normalform müssen über den
Umweg der Berechnung von Polarkoordinaten (Versorform) und der kartesischen
Koordinaten (Normalform) getätigt werden:
Mit Mode + 1 den Taschenrechner in den normalen Modus schalten.
Umrechnung kartesich (Normalform)  polar (Versorform) (z.B. 3 + j4):
- Pol( 3 , 4 ) = eingeben und es wird der Betrag = Länge angezeigt.
- Der Winkel wird mit RCL tan angezeigt.
- Mit RCL cos wird der Betrag angezeigt.
Umrechnung polar (Versorform)  kartesich (Normalform) (z.B. 365 ):
- Shift Pol( 3 , 65 ) = eingeben und es wird der Realanteil = x-Wert angezeigt.
- Der Imaginäranteil = y-Wert wird mit RCL tan angezeigt.
- Mit RCL cos wird der Realanteil angezeigt.
Stand: 8. April 2017
Seite 4-3
Formelsammlung
Elektrotechnik
Gleichheit von komplexen Zahlen:
Zwei komplexe Zahlen sind gleich, wenn ihre Realanteile und ihre Imaginäranteile gleich
sind.
c  a  j b
 c und d sind gleich, wenn a=e und b=f ist.
d e j f
Konjugiert komplexe Zahlen:
Die konjugiert komplexe Zahl wird gebildet, indem man
die komplexe Zahl an der reellen Achse spiegelt.
c = komplexe Zahl
c* = konjugiert komplexe Zahl
In der Normalform:
c  a  j  b  c*  a  j  b
In der trigonometrischen Form:
c  c  cos  j  sin    c*  c  cos  j  sin  
In der Eulerschen Form:
c  c  e j  c*  c  e  j
In der Versorform:
c  c   c*  c   
Addition oder Subtraktion von komplexen Zahlen:
Zur Addition oder Subtraktion von komplexen Zahlen müssen diese in der Normalform
vorliegen !!!
Regel:
Zwei komplexe Zahlen werden addiert bzw. subtrahiert, indem man ihre Realanteile und
ihre Imaginäranteile addiert bzw. subtrahiert.
z1  a  j  b
z 1  z 2  a  c   j  b  d 

z2  c  j  d
z 1  z 2  a  c   j  b  d 
Stand: 8. April 2017
Seite 4-4
Formelsammlung
Elektrotechnik
Multiplikation oder Division von komplexen Zahlen:
Zur Multiplikation oder Division von komplexen Zahlen müssen dies in der
Exponentialform (Eulerform) oder in der Versorform vorliegen !!!
Regel:
- Zwei komplexe Zahlen werden multipliziert, indem man ihre Realanteile multipliziert und
ihre Imaginäranteile addiert.
- Zwei komplexe Zahlen werden dividiert, indem man ihre Realanteile dividiert und ihre
Imaginäranteile subtrahiert.
z1  z1  e
z 1  z 2  z 1  z 2  e j  1 2 
j  1
z2  z2 e
 z1
z 1  e j  1
z1


 e j  1 2 
j  2
z2 z2  e
z2
j  2
z 1  z 2  z 1  z 2 1   2 
z 1  z 1  1
 z1
z1

1   2 
z2 z2
z 2  z 2  2
Definition der Zahl j:
j 2  1
j  1
j3   j
j4 1
j5  j
Multiplikation einer komplexen Zahl mit ihrer konjugiert komplexen Zahl:
Die Multiplikation einer komplexen Zahl mit ihrer konjugiert komplexen Zahl ergibt das
Quadrat des Betrages der komplexen Zahl.
z1  z1*  z1
2
Es entsteht ein rein reelles Ergebnis !!
Inversion einer komplexen Zahl:
Inversion über die Euler- oder Versorform:
z1  z1  e j 
1
1
1
1
1

 e  j


 e  j 
j 
z1 z1
z1 z1  e
z1
Inversion über Normalform und konjugiert komplexer Erweiterung:
a  j  b  a  j  b  a  j  b
1
1


z a  j  b  a  j  b 
a2  b2
a 2  b2
a2  b2
1
a
b
 2
 j 2

2
z a b
a  b2
z  a  j b 
Stand: 8. April 2017
Seite 4-5
Formelsammlung
Elektrotechnik
Vereinbarungen für die Elektrotechnik:
U = komplexe Spannung
U* = konjugiert komplexe Spannung
|U| = U = Betrag der Spannung ( Effektivwert )
φU = Nullphasenwinkel der Spannung
I = komplexer Strom
I* = konjugiert komplexer Strom
|I| = I = Betrag des Stromes ( Effektivwert )
φI = Nullphasenwinkel des Stromes
Grundzweipole in komplexer Darstellung:
Scheinwiderstand Z (Impendanz)
Widerst.
Scheinleitwert Y
Normal
Exponential
Versor
Normal
Exponential
Versor
R
R  e j 0
R0
G
G  e j 0
G0
jL
L  e j 90
L90
1
 e  j 90
L
1
  90
L
jX L
X L  e j 90
X L 90
 jBL
BL  e  j 90
BL   90
1
1
j
jC
C
1
 e  j 90
C
1
  90
C
j C
C  e j 90
C90
 jX C
X C  e  j 90
X C   90
jBC
BC  e j 90
BC 90
1
jL
j
1
L
Spule
Kondens.
  2   f
R = Widerstand in Ω
G = Leitwert in S
L = Induktivität in H
XL = induktiver Blindwiderstand in Ω
BL = induktiver Blindleitwert in Ω
C = Kapazität in F
XC = kapazitiver Blindwiderstand in Ω
BC = kapazitiver Blindleitwert in Ω
1
ω = Kreisfrequenz in
s
f = Frequenz in Hz
Stand: 8. April 2017
Seite 4-6
Formelsammlung
Elektrotechnik
Komplexe Widerstände:
Z
U
I
I
Z
U  e jU
I  e j I
mit   U   I
 Z
U
Z
U  I Z
U
 e j  Z  Z  e j
I
Z  Z  Z  Z  cos  j  sin  
 Z  R  jX
Z = komplexer Widerstand in Ω
U = komplexe Spannung in V
I = komplexer Strom in A
φ = Winkel in °
φU = Spannungs-Nullphasenwinkel in °
φI = Strom-Nullphasenwinkel in °
U = Spannung in V (Betrag von U)
I = Strom in A (Betrag von I)
R = Wirkwiderstand in Ω
X = Scheinwiderstand in Ω
Komplexe Leistung:
S  P  jQ
S  S  e j
S U  I *
cos  
S  Z I
U2
S
Z*
2
P
S
S  S  cos  j  sin  
sin  
Q
S
Die komplexe Leistung errechnet sich aus dem Produkt der komplexen Spannung und des
konjugiert komplexen Stromes.
S = komplexe Leistung
P = Wirkleistung in W
Q = Blindleistung in var
cosφ = Leistungsfaktor
sinφ = Blindfaktor
U = komplexe Spannung
I* = konjugiert komplexer Strom
U = Spannung in V (Betrag von U)
I = Strom in A (Betrag von I)
Z = komplexer Widerstand in Ω
Z* = konjugiert komplexer Widerstand in Ω
Stand: 8. April 2017
Seite 4-7
Formelsammlung
Elektrotechnik
Reihenschaltung komplexer Widerstände:
Z 1  R1  j  X 1
Z g  Z1  Z 2
Z 2  R2  j  X 2
Z g  R1  R2   j   X 1  X 2 
U  U 1 U 2 U1  I  Z1
U2  I  Z2
Zg = komplexer Gesamtscheinwiderstand in Ω
Z1 , Z2 = komplexe Teilscheinwiderstände in Ω
R1, R2 = Teilwirkwiderstände in Ω
X1, X2 = Teilblindwiderstände in Ω
U = komplexe Gesamtspannung in V
I = komplexer Strom in A
Parallelschaltung komplexer Widerstände:
Y
1
Z
G
1
R
B
1
X
Y g  Y1 Y 2 Y 3
Y 1  G1  j  B1
Y 2  G2  j  B2
Y 3  G3  j  B3
Y g  G1  G2  G3   j  B1  B2  B3 
I  I1  I 2  I 3
I1 
U
 U Y 1
Z1
I2 
U
 U Y 2
Z2
I3 
U
 U Y 3
Z3
Y = komplexer Gesamtscheinleitwert in S
Y1, Y2, Y3 = komplexe Teilscheinleitwerte in S
G1, G2, G3 = komplexe Teilwirkleitwerte in S
B1, B2, B3 = komplexe Teilblindleitwerte in S
U = komplexe Gesamtspannung in V
I = komplexer Strom in A
Umwandlung komplexe Reihenschaltung in komplexe Parallelschaltung:
Für die Umwandlung gilt:
Z r  Z p und  r   p und f r  f p
Verfahren der Umwandlung:
- Zg der Reihenschaltung berechnen
und in Versorform umwandeln
1
- Yg von Zg berechnen ( Y g 
) und
Zg
in Normalform umwandeln. Man erhält
die Teil-Leitwerte (G und B).
- Aus den Teil-Leitwerten die Werte der Bauteile berechnen.
Stand: 8. April 2017
Seite 4-8
Formelsammlung
Elektrotechnik
Umwandlung komplexe Parallelschaltung in komplexe Reihenschaltung:
Für die Umwandlung gilt:
Z p  Z r und  p   r und f p  f r
Verfahren der Umwandlung:
- Yg der Parallelschaltung berechnen
und in Versorform umwandeln
1
- Zg von Yg berechnen ( Z g 
) und
Yg
in Normalform umwandeln. Man erhält
die Teil-Widerstände (R und X).
- Aus den Teil-Widerständen die Werte der Bauteile berechnen.
Resonanz:
Von Resonanz wird gesprochen, wenn der imaginäre Anteil des Scheinwiderstandes Z
(Blindwiderstand jX bzw. der Blindleitwert jB) eines Netzwerkes 0 ist.  φ = 0° !!
Die Frequenz, bei der dieser Zustand zutrifft, nennt man Resonanzfrequenz f r oder f0 bzw.
Resonanzkreisfrequenz ωr oder ω0 . Bei Resonanz ist der Scheinwiderstand Z bzw.
der Scheinleitwert Y des Netzwerkes rein reell !!
Reihenresonanz:
fr 
L
1
2   L  C
1
2    f r 2  C
1
LC
r 
L
1
r  C
2
C
1
2    f r 2  L
C
1
r  L
2
Bei Resonanz heben sich UL und UC gegenseitig auf, da sie im Betrag gleich groß und um
180° phasenverschoben sind. Allerdings kann die Spannung an den Bauteilen höher
als die Gesamtspannung U sein (Spannungsüberhöhung)!!
U L UC r  L
1



U
U
R
r  C  R
L
U L  R UC  R

U r U r
C
U L  UC 
r  L U
R

U
r  C  R
U
U

U L r  R UC r  R
fr = Resonanzfrequenz in Hz ; ωr = Resonanzkreisfrequenz in Hz
R = Widerstand in Ω ; L = Induktivität in H ; C = Kapazität in F
U = UR = Spannung am Widerstand in V (Betrag von U = UR)
UL = Spannung an der Spule in V (Betrag von UL)
UC = Spannung am Kondensator in V (Betrag von UC)
U L UC

= Spannungsüberhöhung (Faktor !!)
U
U
Stand: 8. April 2017
Seite 4-9
Formelsammlung
Elektrotechnik
Parallelresonanz:
fr 
1
2   L  C
1
LC
r 
L
1
2    f r 2  C
L
1
r  C
C
1
2    f r 2  L
C
1
r  L
2
2
Bei Resonanz heben sich IL und IC gegenseitig auf, da sie im Betrag gleich groß und um
180° phasenverschoben sind. Allerdings kann der Strom durch die Bauteile höher als
der Gesamtstrom I sein (Stromüberhöhung)!!
I L IC
R


 r  C  R
I
I r  L
L
I R
I R

I L r IC r
I L  IC 
C
IL
I r  R

RI
 r  C  R  I
r  L
IC
I r  R
fr = Resonanzfrequenz in Hz
ωr = Resonanzkreisfrequenz in Hz
R = Widerstand in Ω
L = Induktivität in H
C = Kapazität in F
I = IR = Strom durch Widerstand in V (Betrag von IR)
IL = Strom durch die Spule in V (Betrag von IL)
IC = Strom durch den Kondensator in V (Betrag von IC)
I L IC

= Stromüberhöhung (Faktor !!)
I
I
Stand: 8. April 2017
Seite 4-10
Formelsammlung
Elektrotechnik
Dämpfung:
D
Pe
Pa
Pa 
Pe
D
Pe  D  Pa
D = Dämpfung (Ohne Einheit !!)
Pe = Eingangsleistung in W
Pa = Ausgangsleisung in W
Dämpfungsmaß:
P
a  10  lg e
Pa
Pe  Pa  10
a
10
Pa 
Pe
10
a
10
 Pe  10

a
10
Bei Anpassung (Re = Ra) gilt:
U
a  20  lg e
Ua
a  20  lg
Ie
Ia
U e  U a  10
a
20
Ua 
Ue
10
I e  I a  10
a
20
Ia 
Ie
10
a
20
a
20
 I e  10
 U e  10


a
20
a
20
a = Dämpfungsmaß in dB
Pe = Eingangsleistung in W
Pa = Ausgangsleistung in W
Re = Eingangswiderstand in Ω
Ra = Ausgangswiderstand in Ω
Ue = Eingangsspannung in V
Ua = Ausgangsspannung in V
Ie = Eingangsstrom in A
Ia = Ausgangsstrom in A
Wenn Pa  0,707  Pe entspricht das einer Dämpfung von -3 dB
Das gesamte Dämpfungsmaß ist die Summer der Einzeldämpfungsmaße:
a g  a12  a23  a34
Stand: 8. April 2017
Seite 4-11
Formelsammlung
Elektrotechnik
Komplexe Übertragungsfunktion allgemein:
F  j   
Ua
Ue
Ue 
Ua
F  j  
U a  F  j    U e
F(jω) = komplexe Übertragungsfunktion (Ohne Einheit !!)
Ua = komplexe Ausgangsspannung in V
Ue = komplexe Eingangsspannung in V
Amplituden-Frequenzgang allgemein:
F  j   
Ua
Ue

Ua
Ue
Ue 
Ua
F  j  
U a  F  j    U e
|F(jω)| = Betrag der komplexe Übertragungsfunktion (Ohne Einheit !!)
|Ua| = Ua Betrag der komplexen Ausgangsspannung = Effektivwert der Ausgangsspg. in V
|Ue| = Ue Betrag der komplexen Eingangsspannung = Effektivwert der Eingangsspg. in V
Phasen-Frequenzgang allgemein:
 ImF ( j   

 ReF ( j   
  j     arctan 
φ(jω) = Phasenwinkel der komplexen Übertragungsfunktion
Im{F(jω)} = Imaginäranteil der komplexen Übertragungsfunktion
Re{F(jω)} = Realanteil der komplexen Übertragungsfunktion
Stand: 8. April 2017
Seite 4-12
Formelsammlung
Elektrotechnik
Komplexe Übertragungsfunktion für RC-Tiefpaß:
1
F  j   
1
j   C

1
1 j   R  C
R
j   C
F  j   
1
  R C
 j
2
2
1    R  C 
1    R  C 
Amplituden-Frequenzgang:
Der Amplituden-Frequenzgang ist der Betrag der Übertragungsfunktion.
F  j   
1
1    R  C 
2

1
F  j    dB  20  lg 
 1    R  C 2





für ω  0  |F(jω)|  1  |Ua| = |Ue|
für ω    |F(jω)|  0  |Ua|  0
Phasen-Frequenzgang:
Der Phasen-Frequenzgang ist die Phasendifferenz zwischen Ausgangsspannung und
Eingangsspannung.
  j      arctan   R  C    tan 1   R  C 
für ω = 0  φ(jω) = 0  Ua hat gleiche Phasenlage wie Ue
für ω    φ(jω) = -90°  Ua eilt Ue um 90° nach
Grenzfrequenz:
Bei Grenzfrequenz fg bzw. ωg ist der Wert des Amplituden-Frequenzganges (also der
1
Betrag der Übertragungsfunktion) gleich 0,707 
. Das entspricht –3dB.
2
1
1
1
1
g 
R
C
 fg 
R C
2   R  C
2   f g  C
2   R  f g
Phasenwinkel bei Grenzfrequenz:
  j   g   45  Ua eilt Ue um 45° nach
Stand: 8. April 2017
Seite 4-13
Formelsammlung
Elektrotechnik
Komplexe Übertragungsfunktion für RC-Hochpaß:
F  j   
R
R
1
j   C

j   R  C
1 j   R  C

  R  C 2
  R C
F  j   
 j
2
2
1    R  C 
1    R  C 
Amplituden-Frequenzgang:
Der Amplituden-Frequenzgang ist der Betrag der Übertragungsfunktion.
F  j   
  RC
1    R  C 
2

  RC
F  j    dB  20  lg 
 1    R  C 2





für ω  0  |F(jω)|  0  |Ua|  0
für ω    |F(jω)|  1  |Ua| = |Ue|
Phasen-Frequenzgang:
Der Phasen-Frequenzgang ist die Phasendifferenz zwischen Ausgangsspannung und
Eingangsspannung.
1
1



1 
  tan 

  R C 
  R C 
  j     arctan 
für ω = 0  φ(jω) = +90°  Ua eilt Ue um 90° vor
für ω    φ(jω) = 0°  Ua hat gleiche Phasenlage wie Ue
Grenzfrequenz:
Bei Grenzfrequenz fg bzw. ωg ist der Wert des Amplituden-Frequenzganges (also der
1
Betrag der Übertragungsfunktion) gleich 0,707 
. Das entspricht –3dB.
2
1
1
1
1
g 
R
C
 fg 
R C
2   R  C
2   f g  C
2   R  f g
Phasenwinkel bei Grenzfrequenz:
  j   g   45  Ua eilt Ue um 45° vor
Stand: 8. April 2017
Seite 4-14
Formelsammlung
Elektrotechnik
Komplexe Übertragungsfunktion für RL-Tiefpaß:
F  j   
R

R  j   L
1
1 j  
L
R
L
1
R
F  j   
 j
2
2
L
L


1    
1    
R
R



F  j   
R2
R    L 
2
2
 j
 RL
2
R    L 
2
Amplituden-Frequenzgang:
Der Amplituden-Frequenzgang ist der Betrag der Übertragungsfunktion.
F  j   
1
L

1    
R

2
F  j   
R
R 2    L 
2

R
F  j    dB  20  lg 
 R 2    L 2





für ω  0  |F(jω)|  1  |Ua| = |Ue|
für ω    |F(jω)|  0  |Ua|  0
Phasen-Frequenzgang:
Der Phasen-Frequenzgang ist die Phasendifferenz zwischen Ausgangsspannung und
Eingangsspannung.


L
R


L
R
  j      arctan       tan 1    
für ω = 0  φ(jω) = 0  Ua hat gleiche Phasenlage wie Ue
für ω    φ(jω) = -90°  Ua eilt Ue um 90° nach
Grenzfrequenz:
Bei Grenzfrequenz fg bzw. ωg ist der Wert des Amplituden-Frequenzganges (also der
1
Betrag der Übertragungsfunktion) gleich 0,707 
. Das entspricht –3dB.
2
R
R
R
R  f g  2   L
g 
L
 fg 
L
2   L
2   f g
Phasenwinkel bei Grenzfrequenz:
  j   g   45  Ua eilt Ue um 45° nach
Stand: 8. April 2017
Seite 4-15
Formelsammlung
Elektrotechnik
Komplexe Übertragungsfunktion für RL-Hochpaß:
F  j   
j   L

R  j   L
1
1 j 
R
L
R
1
L
F  j   
 j
2
2
 R 
 R 
1 
1




  L 
  L 
F  j   
  L 2  j    R  L
2
2
R 2    L 
R 2    L 
Amplituden-Frequenzgang:
Der Amplituden-Frequenzgang ist der Betrag der Übertragungsfunktion.
F  j   
1
 R 
1 

  L 
2
F  j   
L
R 2    L 
2

L
F  j    dB  20  lg 
 R 2    L 2





für ω  0  |F(jω)|  0  |Ua|  0
für ω    |F(jω)|  1  |Ua| = |Ue|
Phasen-Frequenzgang:
Der Phasen-Frequenzgang ist die Phasendifferenz zwischen Ausgangsspannung und
Eingangsspannung.
R 
 R 
1 
  tan 

  L 
  L 
  j     arctan 
für ω = 0  φ(jω) = +90°  Ua eilt Ue um 90° vor
für ω    φ(jω) = 0°  Ua hat gleiche Phasenlage wie Ue
Grenzfrequenz:
Bei Grenzfrequenz fg bzw. ωg ist der Wert des Amplituden-Frequenzganges (also der
1
Betrag der Übertragungsfunktion) gleich 0,707 
. Das entspricht –3dB.
2
R
R
R
R  f g  2   L
g 
L
 fg 
L
2   L
2   f g
Phasenwinkel bei Grenzfrequenz:
  j   g   45  Ua eilt Ue um 45° vor
Stand: 8. April 2017
Seite 4-16
Formelsammlung
Elektrotechnik
Frequenznormierte Darstellung der Übertragungsfunktionen (Bode-Diagramm):
Durch die Frequenznormierung erreicht man, das die Darstellung aller Tief- oder
Hochpässe gleich ist und in Abhängigkeit der Grenzfrequenz erfolgt.
Normierung:

f
fg
fg 
f

f    fg


g
g 


    g
Ω = normierte Frequenz (Ohne Einheit)
f = Frequenz in Hz
fg = Grenzfrequenz in Hz
1
ω = Kreisfrequenz in
s
1
ωg = Grenzkreisfrequenz in
s
Tiefpass:
Normierter Amplituden-Frequenzgang:
F  j   

1
F  j   dB  20  lg 
2
 1 
1
1 2
f



fg g
F  j  
2
1




 F  j   d B 



10



f


   10 
fg g
1
Normierter Phasen-Frequenzgang:
  j     arctan    tan 1 
Hochpass:
Normierter Amplituden-Frequenzgang:
F  j   
 
F  j   dB  20  lg 
2
 1 

1 
2
F  j  
f



2
fg g
1  F  j  
2




f



fg g
F  j   dB
10 10
 F  j  dB 
1 - 10 10 




Normierter Phasen-Frequenzgang:
1
1  1 
  tan  


  j     arctan 
Stand: 8. April 2017
Seite 4-17
Formelsammlung
Elektrotechnik
Bode-Diagramme für Tiefpass:
Normierter Amplituden-Frequenzgang:
1
0,9
0,8
0,7
0,6
F  j  
0,5
0,4
0,3
0,2
0,1
0
0,01
0,1
1
10
Ω
100
1000
Normierter Amplituden-Frequenzgang in dB:
0,01
0,1
1
Ω
10
100
1000
0
-10
-20
F  j   dB
-30
-40
-50
-60
-70
Normierter Phasen-Frequenzgang:
0,01
0,1
1
Ω
10
100
1000
0
-10
-20
-30
  j  
-40
-50
-60
-70
-80
-90
Stand: 8. April 2017
Seite 4-18
Formelsammlung
Elektrotechnik
Bode-Diagramme für Hochpass:
Normierter Amplituden-Frequenzgang:
1
0,9
0,8
0,7
0,6
F  j  
0,5
0,4
0,3
0,2
0,1
0
0,001
0,01
0,1
1
Ω
10
100
Normierter Amplituden-Frequenzgang in dB:
0,001
0,01
0,1
Ω
1
10
100
0
-10
-20
F  j   dB
-30
-40
-50
-60
-70
Normierter Phasen-Frequenzgang:
90
80
70
60
50
40
  j   30
20
10
0
0,001
Stand: 8. April 2017
0,01
0,1
Ω
1
10
100
Seite 4-19