Fachhochschule München – Fachbereich 06 – Feinwerktechnik

Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
4. Versuch
Aktives Tiefpaßfilter 1. und 2. Ordnung
Durchführung Seite H - 9
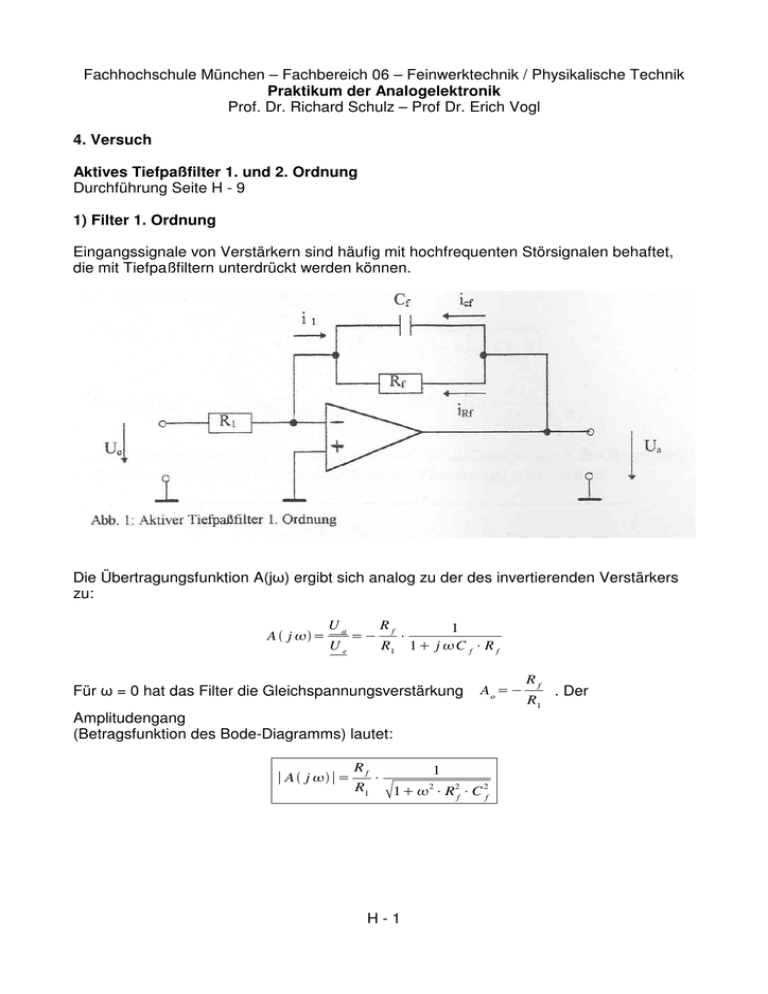
1) Filter 1. Ordnung
Eingangssignale von Verstärkern sind häufig mit hochfrequenten Störsignalen behaftet,
die mit Tiefpaßfiltern unterdrückt werden können.
Die Übertragungsfunktion A(j ) ergibt sich analog zu der des invertierenden Verstärkers
zu:
A j
Für
Ua
Rf
Ue
R1
1
j C f Rf
1
= 0 hat das Filter die Gleichspannungsverstärkung
Ao
Amplitudengang
(Betragsfunktion des Bode-Diagramms) lautet:
A j
Rf
R1
1
1
H-1
2
R2f C 2f
Rf
R1
. Der
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Die obere Grenzfrequenz ( go bzw.
VerstärkungsabfalI auf den Wert:
fgo) des
Filters ist
gegeben
durch den
Ao
A fgo
2
A o = Betrag der Übertragungsfunktion bei f =0
A fgo = Betrag der Übertragungsfunktion bei f = fgo
Es gilt also:
Rf
A
go
Ao
R1
Rf
2
2
R1
1
1
2
go
C 2f R 2f
;
Daraus folgt:
1
go
C f Rf
und
f go
2
1
C f Rf
und somit eine Abnahme der Verstärkung von -20 db/Dekade oder 6 db/Oktave für f>>fgo.
Der Phasenverlauf der Übertragungsfunktion (Phasengang) ergibt sich zu:
arctan
C f Rf
acrtan
1
H-2
C f Rf
180 °
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Man erhält für f = 0 eine Phasenverschiebung von -180°, die für ansteigende Frequenzen
bis auf -270° zunimmt. auf dem Oszilloskop können zunächst natürlich + 180° von -180°
nicht unterschieden werden. Erst die weiteren Phasenmessungen bei höheren
Frequenzen ergeben dann eine eindeutige Aussage.
Die Funktion der Schaltung kann man in einfacher Weise verstehen, wenn man sie als
einen invertierenden Verstärker betrachtet, bei dem der Widerstand Rn durch die
Parallelschaltung von Rf und Cf ersetzt wurde. Der Gesamtwiderstand dieser
Parallelschaltung wird nun mit steigender Frequenz immer kleiner, da der kapazitive
Widerstand des Kondersators abnimmt. Damit geht die Verstärkung ebenfalls zurück und
man erhält das gewünschte Tiefpaßverhalten.
Legt man an den Eingang des Tiefpasses ein nichtsinusförmiges Signal an (z.B.: eine
Rechteckspannung), so kann man mit Hilfe der Übertragungsfunktion nicht direkt die
Antwortfunktion {Ua(t)} berechnen, da diese ja nur für sinusförmige Eingangsspannungen
abgeleitet wurde.
Es bieten sich hier grundsätzlich zwei Lösungsmöglichkeiten an:
1) Man zerlegt die nichtsinusförmige periodische Eingangsspannung in eine Reihe von
sinusförmigen Spannungen (FOURIER-ZERLEGUNG) und berechnet für jede dieser
Spannungen die Antwortfunktion. Die Addition aller Antwortfunktionen liefert dann das
gewünschte Ergebnis.
2) Man stellt die Differentialgleichung des Systems auf und versucht diese zu lösen. Man
erhält damit direkt Ua(t). Bei komplizierten Netzwerken ist es jedoch oft schwierig die
Lösungen der zugehörigen Differentialgleichung zu finden.
Diese zweite Lösungsmöglichkeit wollen wir im Folgenden näher betrachten.
Als Eingangsspannung wollen wir eine sich von Null auf Ue sprunghaft ändernde
Spannung wählen.
H-3
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Es gilt:
i1
Mit
i1
ief
Ue
R1
iRF
;
0 (Knotenpunktgleichung)
ief
dU a
Cf
dt
iRf
;
Ua
Rf
eingesetzt erhält man:
Ue
Cf
R1
dU a
Ua
dt
Rf
0
Diese Differentialgleichung hat folgende Lösung:
t
Ua t
mit U o
Ue Rf
R1
;
C f Rf
Uo
1
1
go
e
1
2
f go
ist gerade die Zeit bei der die Ausgangsspannung Ua(t) auf 63 % des Endwertes
angestiegen ist und wird als Zeitkonstante bezeichnet.
Für f >> fg o oder T (Periodendauer) << kann der Strom iCr im Vergleich zum kapazitiven
Strom iCf vernachlässigt werden, da der kapazitive Widerstand Xc jetzt klein gegenüber
dem Ohm'schen Widerstand Rf ist. Die Differentialgleichung vereinfacht sich jetzt mit iRf =
0 zu:
Ue
R1
Cf
dU a
dt
0
Diese Differentialgleichung kann aber jetzt für "beliebige" Eingangsspannungen Ue(t)
gelöst werden.
H-4
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Die Lösung lautet jetzt:
1
C f R1
Ua t
U e t dt
Uao
Ua o ist dabei der Startwert der Spannung bei t = 0.
Legt man am Eingang eine rechteckförmige Spannung Ue mit T << an, so erhält man am
Ausgang:
Ua t
1
R1 C f
t
U e dt .mit
0
0
t
T
und Uao = 0
4
Die maximale Ausgangsspannung erhält man erstmals für
Sie hat den Wert:
U a max
t
T
.
4
1
T
Ue
R1 C r
4
2) Filter 2. Ordnung
Ein Tiefpaßfilter 2. Ordnung kann im einfachsten Fall aus zwei in Reihe geschalteten
Tiefpässen 1. Ordnung aufgebaut werden.
H-5
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Die Übertragungsfunktion des Gesamtfilters erhält man durch Produktbildung der
Übertragungsfunktionen der Einzelfilter. Dies ist immer der Fall, wenn man die einzelnen
Stufen als entkoppelt betrachten kann. Bei aktiven Filterstufen trifft das praktisch immer
zu, da hier der Ausgangswiderstand einer Filterstufe in der Regel wesentlich kleiner ist als
der Eingangswiderstand der nächstfolgenden Stufe und somit keine Beeinflussung des
Ausgangssignales der Filterstufe erfolgt.
Die Übertragungsfunktion lautet damit:
A j
A1 j
Rf
A2 j
oder:
R1
2
A j
Rf
R
2
1
1
j
C f Rf
1
2
1
1
j
C f Rf
2
Die Grenzfrequenz jeder Einzelstufe beträgt:
f go
2
1
Rf C f
Jede Stufe dämpft bei fgo um -3 db. Die Gesamtdämpfung ist also:
2 (-3 dB) = -6dB
Als Grenzfrequenz wird jedoch die Frequenz betrachtet, bei der insgesamt ein Abfall des
H-6
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Betrages der Übertragungsfunktion von -3 dB vorhanden ist.
3 dB
(Siehe dazu Abb. 8.)
R 2f
A j
1
2
Go
A j0
R
2
1
1
2
.
1
1
j
Go
C f Rf
2
R 2f
R1
Dabei bedeuten
A (j
Go
= Grenzfrequenz des Gesamtfilters.
) = Betrag der Übertragungsfunktion bei der Grenzfrequenz des Gesamtfilters
Go
A o = A (j 0) = Betrag der Übergangsfunktion bei
=0
Nach dem Einsetzen von:
1
go
Rf C f
(Grenzfrequenz der Einzelstufe)
erhält man nach Auflösung der Gleichung:
Go
2
1
go
Die Grenzfrequenz des Gesamtfilters ist also kleiner als die der einzelnen Filterstufen.
Der Abfall der Übertragungsfunktion für f >> fGo erfolgt jetzt mit 2 * 20 dB/Dekade oder
2 * 6 dB/Oktave. Die Übertragungsfunktion hat ein Nennerpolynom 2. Ordnung mit rellen
negativen Lösungen für j . Ein derartiges Filter wird als sogenanntes „kritisches Filter"
H-7
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
bezeichnet, da man als Antwort (Ausgangsspannung) auf eine sich sprungförmig
ändernde Eingangsspannung gerade noch kein Überschwingen über den stationären
Endwert erhält. (Siehe Abb. 10.)
Hat ein Tiefpaßfilter 2. Ordnung im Nennerpolynom komplexe Lösungen für j mit
negativem Realteil, so ist die Übertragungsfunktion etwas verschieden von der bisher
betrachteten (siehe Abb. 9). Die Übertragungsfunktion läßt sich jetzt nach verschiedenen
Gesichtspunkten optimieren.
Man unterscheidet folgende Filtertypen:
a) BUTTERWORTH-FILTER
Der Betrag der Übergangsfunktion verläuft im Durchlaßbereich möglichst lange horizontal
und knickt erst kurz vor
Go scharf ab. Die Sprungantwort zeigt beträchtliches
Überschwingen (Abb. 9).
b) TSCHEBYSCHEFF -FILTER
Im Durchlaßbereich besitzt der Betrag der Übertragungsfunktion eine Welligkeit
konstanter Amplitude, oberhalb der Grenzfrequenz fällt sie noch stärker ab als beim
Butterworth-Filter (Abb. 9). Die Sprungantwort zeigt sehr großes Überschwingen.
c) BESSEL-FILTER
Im Durchlaßbereich ist dieses Filter auf eine möglichst konstante Gruppenlaufzeit
optimiert. (Siehe dazu Versuch 6; Allpaß.) Dieses entspricht einem optimalen
Übertragungsverhalten für Signale die nicht sinusförmig sind. (z.B.: Rechtecks- oder
Dreiecksspannungen.) Oberhalb der Grenzfrequenz knickt die Übertragungsfunktion nicht
so stark wie bei den beiden anderen Filtertypen ab (Abb. 9).
Für die genannten Filtertypen ist eine schaltungstechnische Realisierung beispielsweise in
|1| näher erläutert. Die Reihenschaltung von 2 Filtern 1. Ordnung ergibt immer nur ein
sogenanntes "kritisches" Filter.
H-8
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Kurve 1: Tiefpaß mit kritischer Dämpfung. Kurve 2: Bessel-Tiefpaß. Kurve 3: ButterworthTiefpaß. Kurve 4: Tschebyscheff-Tiefpaß mit 3 dB Welligkeit .
Kurve 1: Tiefpaß mit kritischer Dämpfung. Kurve 2: Bessel-Tiefpaß. Kurve 3: ButterworthTiefpaß. Kurve 4: Tschebyscheff-Tiefpaß mit 0,5 dB Welligkeit. Kurve 5: TschebyscheffTiefpaß mit 3 dB Welligkeit.
3. Versuchsdurchiührung
3.1 Zunächst wird der Operationsverstärker nach Abb. 11 beschaltet.
R1 = Rf= 10 k
Die Gleichspannungsverstärkung lAI wird damit
Rf
R1
1
.
Für Cf keine Elektrolytkondensatoren verwenden, da deren Leckströme eine Fehlerquelle
darstellen!
H-9
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Wählen Sie jetzt eine Grenzfrequenz von fg 0 = 10 000 Hz durch Dimensionierung von Cf
und messen Sie die Amplituden von Ausgangsspannung Ua und Eingangsspannung Ue
von 10 Hz bis 100 KHz (Zweikanal-Oszillograph mißt sie gleichzeitig!) Dabei kann auch
der Phasenunterschied zwischen Ua und Ue bei jedem Meßpunkt aus dem Abstand zweier
gleichartiger Nulldurchgänge bestimmt werden. Die Meßwerte sind anschließend in ein
Bodediagramm einzutragen. Bestimmen Sie fg o aus dem Diagramm! Ebenso wird die
Dämpfung pro Dekade graphisch bestimmt. (mit Ue = 1 V Amplitude.)
3.2 Als nächstes ist ein Filter 2. Ordnung durch Hintereinanderschalten von 2 gleichen
Filtern 1. Ordnung (nach Abb. 7) aufzubauen. Dann sind alle Messungen wie bei 3.1 nach
Abb. 11 zu wiederholen und in die graphische Darstellung einzutragen. Auch fg 0 und die
Dämpfung pro Dekade sind neu zu bestimmen.
3.3 Der dritte Versuch dient der Verwendung als Integrator. Der Versuch wird an einem
Filter 1. Ordnung durchgefuhrt.
So kann eine Rechteckspannung (Generator) in eine Dreiecksspannung umgeformt
werden (1. Integration) und eine Dreiecksspannung in eine nahezu sinusfömlige
Ausgangsspannung (aneinandergereihte Parabelbögen (2. Integration)).
Man verwende als Eingangsspannung das Rechteck-Signal des Generators mit 1,5 V
Amplitude. Betrachten Sie das Ausgangssignal zunächst bei 1 KHz und dann bei 10 KHz.
(Nach der 1. Integration).
Welches C müssen Sie wählen, wenn Sie bei 10 KHz eine annehmbare Dreieckspannung
erhalten wollen? (C = 10 * Cf oder C = 0,1 * Cf?)
H - 10
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Ersetzen Sie jetzt Cf durch den neuen Wert und messen Sie Ue und Ua und fuhren Sie
rechnerisch den Nachweis der folgenden Integration durch:
Ua
1
R1 C f
U e dt
Uao
Anhang zur PC – Simulation
Um die Gleichwertigkeit der Betrachtung des Übertragungsverhaltens eines Tiefpasses im
Ua(t) und im Frequenzraum Ue( )
Ua( ) nachzuprüfen, kann man wie
Zeitraum Ue(t)
folgt vorgehen. Es ist allerdings zu beachten, daß sich die Ausgangsspannung Ua(t) aus
der Lösung der entsprechenden Differentialgleichung des Übertragungsgliedes mit der
Eingangsspannung Ue(t) berechnet und die Ausgangsspannung Ua( ) aus der
Multiplikation der Eingangsspannung Ue( ) mit der Übertragungsfunktion Aj( ).
Ist die Eingangsspannung Ue(t) nicht sinusförmig so kann sie nach Fourier als eine
unendliche Reihe von sinusförmigen Spannungen dargestellt werden. Im weiteren soll
dies an einer rechteckförmigen Eingangsspannung gezeigt werden.
Für eine rechteckförmige Eingangsspannung wie sie nachfolgend dargestellt ist erhält
man folgende Reihe:
Die
einzelnen
sinusförmigen
Eingangsspannungen
werden
nun
mit
der
Übertragungsfunktion Aj( ) multipliziert und ergeben entsprechende sinusförmige
Ausgangsspannungen. Die Summe dieser Ausgangsspannungen ergibt jetzt die
Übertragung einer nichtsinusförmigen Eingangsspannung (im vorliegenden Beispiel eine
Rechteckspannung). In der Praxis muss die unendliche Reihe je nach
Genauigkeitsanforderung natürlich nach dem n-ten Glied abgebrochen werden.
Versuch:
H - 11
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Das genannte Verfahren kann Mithilfe einer Computersimulation anschaulich dargestellt
werden. Dazu muss das Programm "versuch 4.vi" unter "Lab View" aufgerufen werden.
Man erhält wie auf der folgenden Seite dargestellt eine grafische Bedien- und
Anzeigenoberfläche.
Zunächst muss das Programm durch Anklicken (linke Maustaste) des entsprechende
Icons (am Bildrand oben links) gestartet werden. Links sieht man jetzt die Darstellung
einer Rechteckspannung die aus der Grundwelle und den ersten 5 Oberwellen
zusammengesetzt ist.
Jede
dieser
sinusförmigen
Spannungen
wird
jetzt
mit
der
normierten
Übertragungsfunktion A(j ) multipliziert und ergibt eine Ausgangsspannung mit
geänderter Amplitude und Phase.
Die Summe dieser sinusförmigen Ausgangsspannungen ergibt die Ausgangsspannung
des Tiefpasses. Mit der Definition der normierten Frequenz = / o ( o=Grenzfrequenz)
Erhält man für
<<1 proportionales Übertragungsverhalten und für
>>1 die Integration
der Eingangsspannung. Für
~ 1 erhält man eine Mischung aus beiden Grenzfällen.
Mit der Schaltfläche „Frequ. Einstellung" kann mit der linken Maustaste jetzt die normierte
Frequenz
im Bereich von 0,01 bis 10 eingestellt werden. Dabei kann die Änderung der
Amplitude der sinusförmigen Ausgangsspannungen, sowie deren Summe als Funktion
von . Beobachtet werden.
Mit der Schaltfläche „Periodenzahl Einstellung" können eine oder mehrere Perioden der
Ein- und Ausgangsspannung dargestellt werden.
H - 12
Fachhochschule München – Fachbereich 06 – Feinwerktechnik / Physikalische Technik
Praktikum der Analogelektronik
Prof. Dr. Richard Schulz – Prof Dr. Erich Vogl
Bildschirmdarstellung des „Lab View“ Programms:
H - 13