Der Kreis - barth

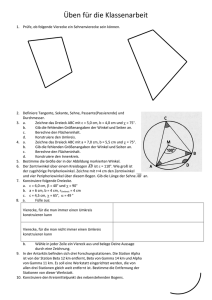
Der Kreis
1.Definition des Kreises und seiner Winkel
2. Lagebeziehungen von Kreis und Gerade
3. Tangentenkonstruktionen
4. Umkreis und Inkreis eines Dreiecks
5. Umkreis bei Vierecken
6. Peripheriewinkelsatz und Zentri – Peripheriewinkelsatz
7. Satz des Thales
8. Umkehrung des Satz des Thales
9. Anwendungen
1. Definition des Kreises und seiner Winkel
Definition:
Eine geometrische Figur, bei der alle Punkte P den gleichen Abstand r zu einem festen
Punkt M besitzen, nennt man Kreis.
M Mittelpunkt des Kreises
r Radius des Kreises
Konstruktion eines Kreises mit dem Radius r=4 cm mit dynageo
d Durchmesser (Verbindungsstrecke zweier Kreispunkte durch den Mittelpunkt
Kreisbogen, Zentriwinkel
M
A
98 °
Zentriwinkel AMB
Kreisausschnitt
Kreisbogen AB
2. Besondere Linien am Kreis
Passante, Sekante, Sehne, Tangente
B
Tangente
Durchmesser
Sekante
Sehne
Passante
Uebung:
3. Konstruktion einer Tangente an einen Kreis
Konstruktion einer Tangente an den Kreis
m
B
A
t
Konstruktionsbeschreibung einfuegen
4. Umkreis und Inkreis am Dreieck
Umkreis
Inkreis
Ein Kreis, der durch die drei Eckpunkte
des Dreiecks geht, heisst Umkreis.
Der Kreis, der die Seiten eines Dreiecks
beruehrt, nennt man Inkreis.
Jedes Dreieck besitzt einen Umkreis.
Der Schnittpunkt der Mittelsenkrechten
ist der Mittelpunkt des Umkreises.
Jedes Dreieck besitzt einen Inkreis. Der
Mittelpunkt des Inkreises ist
Schnittpunkt der Winkelhalbierenden.
Konstruktionen einfuegen mit Konstruktionsbeschreibungen
5. Umkreis bei Vierecken
Definitition:
Ein Viereck, dessen Eckpunkte auf einem Kreis liegen, nennt man Sehnenviereck.
Satz:
In jedem Sehnenviereck sind gegenueberliegende Winkel zusammen 180 Grad gross.
Beweis des Satzes: (siehe Mitschriften)
6. Zentri – Peripheriewinkelsatz
Definition:
Ein Winkel, dessen Scheitelpunkt auf dem Kreis liegt und dessen Schenkel durch die
Kreispunkte A, B gehen, nennt man Peripheriewinkel ueber dem Bogen AB.
Satz:
Wenn zwei Peripheriewinkel ueber dem gleichen Bogen liegen, dann sind die Winkel
gleich gross.
B
34 °
A
34 °
Satz:
Der Zentriwinkel ueber einem Bogen ist doppelt so gross wie jeder Peripheriewinkel
ueber demselben Bogen.
60 °
120 °
Anwenden der Saetze
- Konstruktion von Sehnen
1. Gegeben ist ein Kreis mit dem Radius 2,5 cm. Konstruiere eine Sehne AB, zu
der der Peripheriewinkel ueber dem Bogen AB von 70 Grad gehoert.
2. Zeichne einen Kreis mit r= 3cm. Konstruiere eine Sehne AB des Kreises, so
dass fuer den Peripheriewinkel  ueber dem Bogen AB gilt:
=80 Grad
3. Zeichne eine Strecke AB der angegebenen Laenge. Konstruiere dann einen
Kreis mit AB als Sehne so, dass die Peripheriewinkel ueber dem Bogen AB die
Groesse  besitzen.
-
Sehwinkel
Die Wandtafel ist 4 m lang. Ermittle durch Konstruktion alle Punkte, von denen
aus man die Tafel unter einem Sehwinkel von 30 Grad sieht.
Weitere Uebungen
4. Konstruiere zum Dreieck A(2;3) B(7:4) und C(5;-2) den Umkreis und den Inkreis.
5. Konstruiere zum Kreis mit dem Mittelpunkt M(-10;1) und dem Radius 5 durch den
Punkt (-6;4) die Tangente.
6. Gegeben ist ein Kreis mit dem Mittelpunkt M (0;7) und dem Radius 5.
Der Punkt A hat die Koordinaten (0;2),  ist 70 Grad, die Sehne AB hat die Laenge 3cm,
 ist 80 Grad.
Konstruiere das Sehnenviereck.