1. SA

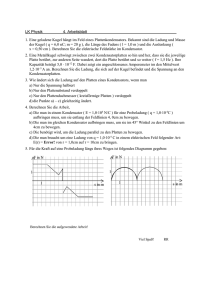
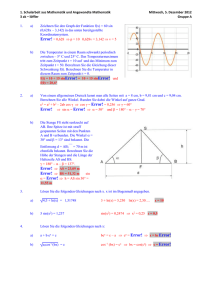
1. Schularbeit aus Mathematik und angewandter Mathematik
2 ck – hiebaum
1.
Vereinfachen Sie so weit wie möglich und stellen Sie die Resultate gegebenenfalls als Wurzeln und ohne
negativen Exponenten dar:
a)
b)
c)
2.
a)
b)
c)
3.
4.
Montag, 23. November 2015
Gruppe A
a)
3;x5 ⋅
6;x5 =
Error! =
4;x
3;x2 =
x5
Error!
12;x5
NR Error! + Error! = Error! =
NR: 2 + Error! = Error!
NR:
Error!
Error! = Error!
Das Volumen eines Zylinders ist V = r2 π h. r ist der Radius, h seine Höhe, V das Volumen des Zylinders.
Berechnen Sie um welchen Prozentsatz sich das Volumen ändert, wenn man den Radius um 30 % größer
und die Höhe um 30 % kleiner macht.
Faktor für V = 1,32 ⋅ 0,7 = 1,183
Das Volumen wird um 18,3 % größer.
Drei Größen A, B und C haben den Zusammenhang C = A2 B3. Stellen Sie die Formel nach der
Variablen A um.
K5 = a 2 m
Error! = A2 ⇒ A = Error!
a0
K= 5
Zwei der in der Tabelle angegebenen Formeln entsprechen der Formel
;m
K = Error!.
K = a0,4 m–0,2
X
Kreuzen Sie die zutreffenden Formeln an:
K=
X
Lösen Sie das System über ℝ:
2
–1
5;a m
7x + 3y = 50
7x + 3y = 50
38x = –304 ⇒ x = 8 und y = –2
K = a0,4 m0,2
2y = 8x – 68
–8x +2y = –68
b)
Lösen Sie das System:
2x + 3y = 12
und x – y = 1
grafisch:
c)
Geben Sie den Wert des Parameters a an, für den
das System:
a x + 7 y = 50
20 x + 70 y = 500
unendlich viele Lösungen hat.
a=2
a)
Eine Boutiquebesitzerin kauft 80 Stk. des Modells A und 25 Stk. von Modell B und zahlt dafür € 12.150,-.
Bei der nächsten Bestellung kauft sie nur 30 Stk. von Modell A und 20 Stk. von Modell B. Sie handelt
aber den Preis von A um 20 % und den Preis von B um 10 % herunter und zahlt dann € 4.380,--. Erstellen
Sie ein Gleichungssystem für die Berechnung der Preise der beiden Modelle und berechnen Sie die
ursprünglichen und die reduzierten Preise.
80 a + 25 b = 12 150
80a + 25b = 12 150
a = 130 (104)
30 a 0,8 + 20 b 0,9 = 4 380
24a + 18b = 4 380
b = 70 (63)
Ein Güterzug verlässt den Ort Achenkirchen um 8:30 und fährt mit einer Geschwindigkeit von 60 km/h.
Um 10:00 fährt der Personenzug mit 100 km/h in die gleiche Richtung. Zum Glück ist die Strecke
zweigleisig. Stellen Sie die Bewegungsgleichungen der beiden Züge auf. Benutzen Sie das
Koordinatensystem: s = 0 ist Achenkirchen, Bewegung in positiver s-Richtung, t ist die Uhrzeit in
Stunden.
Berechnen Sie, wann (Uhrzeit) und wo (Entfernung von Achenkirchen) der Personenzug den Güterzug
überholt.
sg = 60(t – 8,5)
s = 60t – 510
sp = 100(t – 10)
s = 100t – 1000 ⇒ s = 225 ∧ t = 12,25
b)
Der Personenzug überholt den Güterzug um 12:15 225 km von Achenkirchen entfernt.
1. Schularbeit aus Mathematik und angewandter Mathematik
2 ck – hiebaum
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
Montag, 23. November 2015
Gruppe B
1.
2.
Vereinfachen Sie so weit wie möglich und stellen Sie die Resultate gegebenenfalls als Wurzeln und ohne
negativen Exponenten dar:
a)
4;x5 ⋅ 8;x5 =
8;x15
NR Error! + Error! = Error!
b)
Error! =
Error!
NR: 4 + Error! = Error!
c)
a)
b)
c)
3.
a)
b)
c)
4.
a)
b)
5;x 3;x2 =
15;x5
NR: Error! = Error!
Das Volumen eines Zylinders ist V = r2 π h. r ist der Radius, h seine Höhe, V das Volumen des Zylinders.
Berechnen Sie um welchen Prozentsatz sich das Volumen ändert, wenn man den Radius um 50 % größer
und die Höhe um 50 % kleiner macht.
Faktor für V = 1,52 ⋅ 0,5 = 1,125
Das Volumen wird um 12,5 % größer.
Drei Größen A, B und C haben den Zusammenhang C = A3 B2. Stellen Sie die Formel nach der
Variablen A um.
K5 = a 2 m
Error! = A3 ⇒ A = Error!
a0
Zwei der in der Tabelle angegebenen Formeln entsprechen der Formel
K= 5
;m
K = Error!.
K = a0,4 m–0,2
x
Kreuzen Sie die zutreffenden Formeln an:
K=
x
2
–1
5;a m
Lösen Sie das System über ℝ:
K
= a0,4 m0,2
7x + 3y = 50
7x + 3y = 50
38x = –304 ⇒ x = 7 und y =
–2
2y = 8x – 68
–8x +2y = –68
Lösen Sie das System:
2x + 3y = 12
und x – y = 1
grafisch:
Geben Sie den Wert des Parameters a an, für den
das System:
a x + 7 y = 50
20 x + 70 y = 500
unendlich viele Lösungen hat.
a=2
Eine Boutiquebesitzerin kauft 80 Stk. des Modells A und 20 Stk. von Modell B und zahlt dafür € 10.800,-.
Bei der nächsten Bestellung kauft sie nur 30 Stk. von Modell A und 20 Stk. von Modell B. Sie handelt
aber den Preis von A um 20 % und den Preis von B um 10 % herunter und zahlt dann € 3.960,--. Erstellen
Sie ein Gleichungssystem für die Berechnung der Preise der beiden Modelle und berechnen Sie die
ursprünglichen und die reduzierten Preise.
80 a + 20 b = 10 800
80a + 25b = 12 150
a = 120 (96)
30 a 0,8 + 20 b 0,9 = 3 960
24a + 18b = 3 960
b = 60 (54)
Ein Güterzug verlässt den Ort Achenkirchen um 9:30 und fährt mit einer Geschwindigkeit von 60 km/h.
Um 10:00 fährt der Personenzug mit 100 km/h in die gleiche Richtung. Zum Glück ist die Strecke
zweigleisig. Stellen Sie die Bewegungsgleichungen der beiden Züge auf. Benutzen Sie das
Koordinatensystem: s = 0 ist Achenkirchen, Bewegung in positiver s-Richtung, t ist die Uhrzeit in
Stunden.
Berechnen Sie, wann (Uhrzeit) und wo (Entfernung von Achenkirchen) der Personenzug den Güterzug
überholt.
sg = 60(t – 9,5)
s = 60t – 570
sp = 100(t – 10)
s = 100t – 1000 ⇒ s = 75 ∧ t = 10,75
Der Personenzug überholt den Güterzug u
m 10:45 75 km von Achenkirchen entfernt.
1. Schularbeit aus Mathematik und angewandter Mathematik
2 ck – hiebaum
Montag, 23. November 2015
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
Vereinfachen Sie so weit wie möglich und stellen Sie die Resultate gegebenenfalls als Wurzeln und ohne
negativen Exponenten dar:
a)
3;x5 ⋅
b)
Error! =
c)
2.
4;x
6;x5 =
3;x2 =
a)
Das Volumen eines Zylinders ist V = r2 π h. r ist der Radius, h seine Höhe, V das Volumen des Zylinders.
Berechnen Sie um welchen Prozentsatz sich das Volumen ändert, wenn man den Radius um 30 % größer
und die Höhe um 30 % kleiner macht.
b)
Drei Größen A, B und C haben den Zusammenhang C = A2 B3.
Stellen Sie die Formel nach der Variablen A um.
c)
Zwei der in der Tabelle angegebenen Formeln entsprechen der Formel
K = Error!.
Kreuzen Sie die zutreffenden Formeln an:
K5 = a 2 m
a0
K= 5
;m
K = a0,4 m–0,2
K=
5;a2 m–1
K = a0,4 m0,2
A
3.
4.
a)
Lösen Sie das System über ℝ:
7x + 3y = 50
2y = 8x – 68
b)
Lösen Sie das System:
2x + 3y = 12
und x – y = 1
grafisch:
c)
Geben Sie den Wert des Parameters a an, für den das
System:
a x + 7 y = 50
20 x + 70 y = 500
unendlich viele Lösungen hat.
a)
Eine Boutiquebesitzerin kauft 80 Stk. des Modells A und 25 Stk. von Modell B und zahlt dafür € 12.150,-.
Bei der nächsten Bestellung kauft sie nur 30 Stk. von Modell A und 20 Stk. von Modell B. Sie handelt
aber den Preis von A um 20 % und den Preis von B um 10 % herunter und zahlt dann € 4.380,--. Erstellen
Sie ein Gleichungssystem für die Berechnung der Preise der beiden Modelle und berechnen Sie die
ursprünglichen und die reduzierten Preise.
b)
Ein Güterzug verlässt den Ort Achenkirchen um 8:30 und fährt mit einer Geschwindigkeit von 60 km/h.
Um 10:00 fährt der Personenzug mit 100 km/h in die gleiche Richtung. Zum Glück ist die Strecke
zweigleisig. Stellen Sie die Bewegungsgleichungen der beiden Züge auf. Benutzen Sie das
Koordinatensystem: s = 0 ist Achenkirchen, Bewegung in positiver s-Richtung, t ist die Uhrzeit in
Stunden.
Berechnen Sie, wann (Uhrzeit) und wo (Entfernung von Achenkirchen) der Personenzug den Güterzug
überholt.
1. Schularbeit aus Mathematik und angewandter Mathematik
2 ck – hiebaum
Montag, 23. November 2015
Gruppe B
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
Vereinfachen Sie so weit wie möglich und stellen Sie die Resultate gegebenenfalls als Wurzeln und ohne
negativen Exponenten dar:
a)
4;x5 ⋅ 8;x5 =
b)
c)
2.
Error! =
5;x
3;x2 =
a)
Das Volumen eines Zylinders ist V = r2 π h. r ist der Radius, h seine Höhe, V das Volumen des Zylinders.
Berechnen Sie um welchen Prozentsatz sich das Volumen ändert, wenn man den Radius um 50 % größer
und die Höhe um 50 % kleiner macht.
b)
Drei Größen A, B und C haben den Zusammenhang C = A3 B2. Stellen Sie die Formel nach der
Variablen A um.
c)
Zwei der in der Tabelle angegebenen Formeln entsprechen der Formel
K = Error!.
Kreuzen Sie die zutreffenden Formeln an:
K5 = a 2 m
a0
K= 5
;m
0,4
K = a m–0,2
K=
5;a2 m–1
K = a0,4 m0,2
B
3.
4.
a)
Lösen Sie das System über ℝ:
7x + 3y = 50
2y = 8x – 68
b)
Lösen Sie das System:
2x + 3y = 12
und x – y = 1
grafisch:
c)
Geben Sie den Wert des Parameters a an, für den das System:
a x + 7 y = 50
20 x + 70 y = 500
unendlich viele Lösungen hat.
a)
Eine Boutiquebesitzerin kauft 80 Stk. des Modells A und 20 Stk. von Modell B und zahlt dafür € 10.800,-.
Bei der nächsten Bestellung kauft sie nur 30 Stk. von Modell A und 20 Stk. von Modell B. Sie handelt
aber den Preis von A um 20 % und den Preis von B um 10 % herunter und zahlt dann € 3.960,--. Erstellen
Sie ein Gleichungssystem für die Berechnung der Preise der beiden Modelle und berechnen Sie die
ursprünglichen und die reduzierten Preise.
b)
Ein Güterzug verlässt den Ort Achenkirchen um 9:30 und fährt mit einer Geschwindigkeit von 60 km/h.
Um 10:00 fährt der Personenzug mit 100 km/h in die gleiche Richtung. Zum Glück ist die Strecke
zweigleisig. Stellen Sie die Bewegungsgleichungen der beiden Züge auf. Benutzen Sie das
Koordinatensystem: s = 0 ist Achenkirchen, Bewegung in positiver s-Richtung, t ist die Uhrzeit in
Stunden.
Berechnen Sie, wann (Uhrzeit) und wo (Entfernung von Achenkirchen) der Personenzug den Güterzug
überholt.