3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997

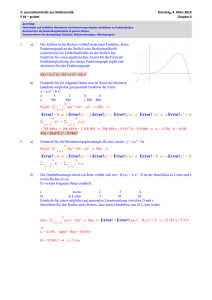
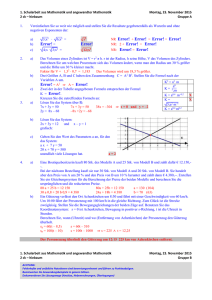
3. Lernzielkontrolle aus Mathematik
5 ck – hiebaum
Dienstag, 18. Februar 2014
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
a)
Der Zufluss in ein Becken verläuft nach einer Funktion,
deren Funktionsgraph wie in der Grafik verläuft:
Ermitteln Sie einen algebraischen Ansatz für die Form der
Funktionsgleichung, der diesen Funktionsgraph ergibt.
f(x) = a x (x – k)2 = a x3 + b x2 + c x
b)
Ermitteln Sie für folgende Daten eine im Sinne der
kleinsten Quadrate möglichst gut passende Funktion der
Form:
y = a x3 + b x
x
2
4
6
y
900
1.200 800
4
F(a,b) =  ;
; (axi3 + bx – yi)2  Min 
i=1
Error! = 0  a Error!ti6 + b Error!xi4 =
4
Error!yi xi3 ∧ Error! = 0  a Error!xi4 + b
4
;
; xi2 =  ;
; yi xi
i=1
i=1
50 816 a + 1 568 b = 256 800 ∧ 1 568 a + 56 b = 11 400  a = –9,03 b = 456,35
P(t) = 456 t – 9,03 t3
2.
a)
Kreuzen Sie den Wahrheitsgehalt der folgenden Aussagen an:
wahr
Bei der Methode der kleinsten Quadrate werden die Abweichungen der y-Werte
(gerechnet – tatsächlich) quadriert, damit das Vorzeichen der Differenz immer positiv
ist
Alle partiellen Ableitungen der Funktion F(a, b, …) =  (Y – y)2 müssen gleich Null
sein, weil möglichst viele Differenzen Y – y gleich Null sein müssen
Für die optimalen Parameter a, b, … der Funktion F(a, b, …) = (Y – y)2 sind alle
partiellen Ableitungen gleich 0
b)
falsch
x
x
x
Ermitteln Sie mit Hilfe der Methode der kleinsten Quadrate eine möglichst gut passende Funktion der
Form R(s) = Error! aus folgenden Daten. Berechnen Sie insbesondere den Faktor k.
s
5
10
15
R
1.000
2.000
10.000
3
F(a) =  ;
; (a si3 – Ri)2  Min  Error! = Error!2 (a si3 – Ri) si3 = 0  12 406 250 a = 35
i=1
875 000 
s3;0
a = 2,892 k = 0,35 daher R(s) =
35
A
3.
4.
a)
Eine Firma ermittelt für ein Produkt den Zusammenhang zwischen Werbeaufwand w und abgesetzter
Menge q:
w
in 100 000 EUR 2
2,5
3
4
q
in 1 000 Stk.
30
50
55
58
Ermitteln Sie eine möglichst gut passende Funktion der Form q(w) = aw2 + bw
392,06 a + 114,63 b = 1 855,5 ∧ 114,63 a + 35,25 b = 582  q(w) = 22,74 w – 1,92 w2
b)
Die Funktion für die Situation in 3.a) laute: q(w) = 20 w – 2 w2. Einheiten wie in 3.a)
Berechnen Sie, ab welchem Werbeaufwand in Euro die abgesetzte Menge wieder sinken würde. Geben
Sie ein vernünftiges Intervall (in Euro) für die Validität (Gültigkeit) des Modells an. Berechnen Sie den
Grenznutzen eines Werbe-Euros (also die Zunahme des Absatzes in Stk. pro eingesetztem Euro) bei
einem schon erreichten Absatz von 48 000 Stk..
Error! = 20 – 4w = 0  w = 5 also w ∈ [0 / 5] 48 = 20w – 2w2  w = 4 als relevante Lösung
Error!(4) = 16
= Error!pc/EUR = 0,04 Stk. pro EUR
Ab einem Werbeaufwand von EUR 500 000,-- würden in diesem Modell die Absätze wieder sinken. Für
ein valides Modell sollte also w ≤ 5 sein. Grundsätzlich sollten Berechnungen nicht aus dem Bereich von
EUR 200 000,-- bis EUR 400.000 herausfallen, weil man dann extrapolieren würde.
Um bei einem Absatz von 48 000 Stk. einen Mehrabsatz von 40 Stk. zu erzielen, ist ein Mehraufwand
von EUR 1.000,-- notwendig.
a)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten
Abfluss.
Skizzieren Sie den Funktionsverlauf unter
Berücksichtigung der Nullstellen.
Berechnen Sie den maximalen Zufluss.
Error!= 6 (3t2 – 60t + 200) = 0 
t1 = 4,226 und t2 = 15,774
z(4,226) = 2 309,4
Der maximale Zufluss beträgt 2 309,4 ME/d.
b)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Berechnen Sie eine Gleichung für die Gesamtmenge M im Becken, wenn M(0) = 1 000 ME war.
Berechnen Sie, ob das Becken leer wird. Wenn ja, berechnen Sie den Zeitpunkt, wenn nein, berechnen
Sie die Restmenge zum Zeitpunkt t = 20.
Zusatz (3 Punkte): Begründen Sie, warum man diesen Wert auch ohne Rechnung ermitteln kann.
M(t) = Error! = 1,5 t4 – 60 t3 + 1 200 t2 + C mit M(0) = 1 000 = C
M(t) hat keine Nullstellen, M(20) = 1 000 ME
Das Becken wird nicht leer, die Restmenge ist genau so groß wie die Anfangsmenge (1 000 ME),
weil in den ersten 10 Tagen so viel Wasser zuläuft, wie in den letzten 10 Tage abläuft (die Flächen
unterhalb des Funktionsgraphen von z(t) zwischen 0 und 10 und zwischen 10 und 20 sind gleich
groß.
3. Lernzielkontrolle aus Mathematik
5 ck – hiebaum
Dienstag, 18. Februar 2014
Gruppe B
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
a)
Der Zufluss in ein Becken verläuft nach einer Funktion,
deren Funktionsgraph wie in der Grafik verläuft:
Ermitteln Sie einen algebraischen Ansatz für die Form der
Funktionsgleichung, der diesen Funktionsgraph ergibt.
f(x) = a x (x – k)2 = a x3 + b x2 + c x
b)
Ermitteln Sie für folgende Daten eine im Sinne der kleinsten Quadrate möglichst gut passende Funktion der Form:
y = a x3 + b x
x
2
4
6
y
9.000 12.000
8.000
4
F(a,b) =  ;
; (axi3 + bx – yi)2  Min 
i=1
Error! = 0  a Error!ti6 + b Error!xi4 =
4
Error!yi xi3 ∧ Error! = 0  a Error!xi4 + b
4
;
; xi2 =  ;
; yi xi
i=1
i=1
50 816 a + 1 568 b = 2 568 000 ∧ 1 568 a + 56 b = 114 000  a = –90,3 b = 4 563,5
P(t) = 4 564 t – 90,3 t3
2.
a)
Kreuzen Sie den Wahrheitsgehalt der folgenden Aussagen an:
wahr
Bei der Methode der kleinsten Quadrate werden die Abweichungen der y-Werte
(gerechnet – tatsächlich) quadriert, weil sonst die partiellen Ableitungen der Funktion
F(a, b, …) nicht Null würden.
Alle partiellen Ableitungen der Funktion F(a, b, …) =  (Y – y)2 müssen gleich Null
sein, weil man ein Minimum der Funktion F(a, b, …) sucht.
Für die optimalen Parameter a, b, … der Funktion F(a, b, …) = (Y – y)2 sind alle
partiellen Ableitungen positiv
b)
falsch
x
x
x
Ermitteln Sie mit Hilfe der Methode der kleinsten Quadrate eine möglichst gut passende Funktion der
Form R(s) = Error! aus folgenden Daten. Berechnen Sie insbesondere den Faktor k.
s
5
10
15
R
100
200
1.000
3
F(a) =  ;
; (a si3 – Ri)2  Min  Error! = Error!2 (a si3 – Ri) si3 = 0  12 406 250 a = 3
i=1
587 500 
s3;3
a = 0,2892 k = 3,5 daher R(s) =
5
B
3.
4.
a)
Eine Firma ermittelt für ein Produkt den Zusammenhang zwischen Werbeaufwand w und abgesetzter
Menge q:
w
in 100 000 EUR 2
2,5
3
4
q
in 1 000 Stk.
30
50
55
58
Ermitteln Sie eine möglichst gut passende Funktion der Form q(w) = aw2 + bw
392,06 a + 114,63 b = 1 855,5 ∧ 114,63 a + 35,25 b = 582  q(w) = 22,74 w – 1,92 w2
b)
Die Funktion für die Situation in 3.a) laute: q(w) = 20 w – w2. Einheiten wie in 3.a)
Berechnen Sie, ab welchem Werbeaufwand in Euro die abgesetzte Menge wieder sinken würde. Geben
Sie ein vernünftiges Intervall (in Euro) für die Validität (Gültigkeit) des Modells an. Berechnen Sie den
Grenznutzen eines Werbe-Euros (also die Zunahme des Absatzes in Stk. pro eingesetztem Euro) bei
einem schon erreichten Absatz von 84 000 Stk..
Error! = 20 – 2w = 0  w = 10 also w ∈ [0 / 10] 84 = 20w – w2  w = 6 als relevante Lösung
Error!(6) = 8
= Error!pc/EUR = 0,0133 Stk. pro EUR
Ab einem Werbeaufwand von EUR 1 000 000,-- würden in diesem Modell die Absätze wieder sinken.
Für ein valides Modell sollte also w ≤ 10 sein. Grundsätzlich sollten Berechnungen nicht aus dem
Bereich von EUR 200 000,-- bis EUR 400.000 herausfallen, weil man dann extrapolieren würde.
Um bei einem Absatz von 84 000 Stk. einen Mehrabsatz von 13,3 Stk. zu erzielen, ist ein Mehraufwand
von EUR 1.000,-- notwendig.
a)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten
Abfluss.
Skizzieren Sie den Funktionsverlauf unter
Berücksichtigung der Nullstellen.
Berechnen Sie den maximalen Zufluss.
Error!= 6 (3t2 – 60t + 200) = 0 
t1 = 4,226 und t2 = 15,774
z(4,226) = 2 309,4
Der maximale Zufluss beträgt 2 309,4 ME/d.
b)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Berechnen Sie eine Gleichung für die Gesamtmenge M im Becken, wenn M(0) = 1 000 ME war.
Berechnen Sie, ob das Becken leer wird. Wenn ja, berechnen Sie den Zeitpunkt, wenn nein, berechnen
Sie die Restmenge zum Zeitpunkt t = 20.
Zusatz (3 Punkte): Begründen Sie, warum man diesen Wert auch ohne Rechnung ermitteln kann.
M(t) = Error! = 1,5 t4 – 60 t3 + 1 200 t2 + C mit M(0) = 1 000 = C
M(t) hat keine Nullstellen, M(20) = 1 000 ME
Das Becken wird nicht leer, die Restmenge ist genau so groß wie die Anfangsmenge (1 000 ME),
weil in den ersten 10 Tagen so viel Wasser zuläuft, wie in den letzten 10 Tage abläuft (die Flächen
unterhalb des Funktionsgraphen von z(t) zwischen 0 und 10 und zwischen 10 und 20 sind gleich
groß.
3. Lernzielkontrolle aus Mathematik
5 ck – hiebaum
Dienstag, 18. Februar 2014
Gruppe A
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
2.
a)
Der Zufluss in ein Becken verläuft nach einer Funktion,
deren Funktionsgraph wie in der Grafik verläuft:
Ermitteln Sie einen algebraischen Ansatz für die Form der
Funktionsgleichung, der diesen Funktionsgraph ergibt.
b)
Ermitteln Sie für folgende Daten eine im Sinne der kleinsten Quadrate möglichst gut passende Funktion der Form:
y = a x3 + b x
x
2
4
6
y
900
1.200 800
a)
Kreuzen Sie den Wahrheitsgehalt der folgenden Aussagen an:
wahr
falsch
Bei der Methode der kleinsten Quadrate werden die Abweichungen der y-Werte
(gerechnet – tatsächlich) quadriert, damit das Vorzeichen der Differenz immer positiv
ist
Alle partiellen Ableitungen der Funktion F(a, b, …) =  (Y – y)2 müssen gleich Null sein,
weil möglichst viele Differenzen Y – y gleich Null sein müssen
Für die optimalen Parameter a, b, … der Funktion F(a, b, …) = (Y – y)2 sind alle
partiellen Ableitungen gleich 0
3.
4.
b)
Ermitteln Sie mit Hilfe der Methode der kleinsten Quadrate eine möglichst gut passende Funktion der
Form R(s) = Error! aus folgenden Daten. Berechnen Sie insbesondere den Faktor k.
s
5
10
15
R
1.000
2.000
10.000
a)
Eine Firma ermittelt für ein Produkt den Zusammenhang zwischen Werbeaufwand w und abgesetzter
Menge q:
w
in 100 000 EUR 2
2,5
3
4
q
in 1 000 Stk.
30
50
55
58
Ermitteln Sie eine möglichst gut passende Funktion der Form q(w) = aw2 + bw
b)
Die Funktion für die Situation in 3.a) laute: q(w) = 20 w – 2 w2. Einheiten wie in 3.a)
Berechnen Sie, ab welchem Werbeaufwand in Euro die abgesetzte Menge wieder sinken würde. Geben
Sie ein vernünftiges Intervall (in Euro) für die Validität (Gültigkeit) des Modells an. Berechnen Sie den
Grenznutzen eines Werbe-Euros (also die Zunahme des Absatzes in Stk. pro eingesetztem Euro) bei
einem schon erreichten Absatz von 48 000 Stk..
a)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Skizzieren Sie den Funktionsverlauf unter Berücksichtigung der Nullstellen.
Berechnen Sie den maximalen Zufluss.
b)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Berechnen Sie eine Gleichung für die Gesamtmenge M im Becken, wenn M(0) = 1 000 ME war.
Berechnen Sie, ob das Becken leer wird. Wenn ja, berechnen Sie den Zeitpunkt, wenn nein, berechnen
Sie die Restmenge zum Zeitpunkt t = 20.
Zusatz (3 Punkte): Begründen Sie, warum man diesen Wert auch ohne Rechnung ermitteln kann.
3. Lernzielkontrolle aus Mathematik
5 ck – hiebaum
Dienstag, 18. Februar 2014
Gruppe B
ACHTUNG:
Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen.
Beantworten Sie Anwendungsbeispiele in ganzen Sätzen.
Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen)
1.
2.
a)
Der Zufluss in ein Becken verläuft nach einer Funktion,
deren Funktionsgraph wie in der Grafik verläuft:
Ermitteln Sie einen algebraischen Ansatz für die Form der
Funktionsgleichung, der diesen Funktionsgraph ergibt.
b)
Ermitteln Sie für folgende Daten eine im Sinne der kleinsten Quadrate möglichst gut passende Funktion der Form:
y = a x3 + b x
x
2
4
6
y
9.000 12.000
8.000
a)
Kreuzen Sie den Wahrheitsgehalt der folgenden Aussagen an:
wahr
falsch
Bei der Methode der kleinsten Quadrate werden die Abweichungen der y-Werte
(gerechnet – tatsächlich) quadriert, weil sonst die partiellen Ableitungen der Funktion
F(a, b, …) nicht Null würden.
Alle partiellen Ableitungen der Funktion F(a, b, …) =  (Y – y)2 müssen gleich Null sein,
weil man ein Minimum der Funktion F(a, b, …) sucht.
Für die optimalen Parameter a, b, … der Funktion F(a, b, …) = (Y – y)2 sind alle
partiellen Ableitungen positiv
3.
4.
b)
Ermitteln Sie mit Hilfe der Methode der kleinsten Quadrate eine möglichst gut passende Funktion der
Form R(s) = Error! aus folgenden Daten. Berechnen Sie insbesondere den Faktor k.
s
5
10
15
R
100
200
1.000
a)
Eine Firma ermittelt für ein Produkt den Zusammenhang zwischen Werbeaufwand w und abgesetzter
Menge q:
w
in 100 000 EUR 2
2,5
3
4
q
in 1 000 Stk.
30
50
55
58
Ermitteln Sie eine möglichst gut passende Funktion der Form q(w) = aw2 + bw
b)
Die Funktion für die Situation in 3.a) laute: q(w) = 20 w – w2. Einheiten wie in 3.a)
Berechnen Sie, ab welchem Werbeaufwand in Euro die abgesetzte Menge wieder sinken würde. Geben
Sie ein vernünftiges Intervall (in Euro) für die Validität (Gültigkeit) des Modells an. Berechnen Sie den
Grenznutzen eines Werbe-Euros (also die Zunahme des Absatzes in Stk. pro eingesetztem Euro) bei
einem schon erreichten Absatz von 84 000 Stk..
a)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Skizzieren Sie den Funktionsverlauf unter Berücksichtigung der Nullstellen.
Berechnen Sie den maximalen Zufluss.
b)
Der Zu- und Abfluss in bzw. aus einem Staubecken erfolgt mit z(t) = 6 t (10 – t) (20 – t) für 0 ≤ t ≤ 20.
t in Tagen, z in ME/d. Negative Werte von z bedeuten Abfluss.
Berechnen Sie eine Gleichung für die Gesamtmenge M im Becken, wenn M(0) = 1 000 ME war.
Berechnen Sie, ob das Becken leer wird. Wenn ja, berechnen Sie den Zeitpunkt, wenn nein, berechnen
Sie die Restmenge zum Zeitpunkt t = 20.
Zusatz (3 Punkte): Begründen Sie, warum man diesen Wert auch ohne Rechnung ermitteln kann.