1. SA

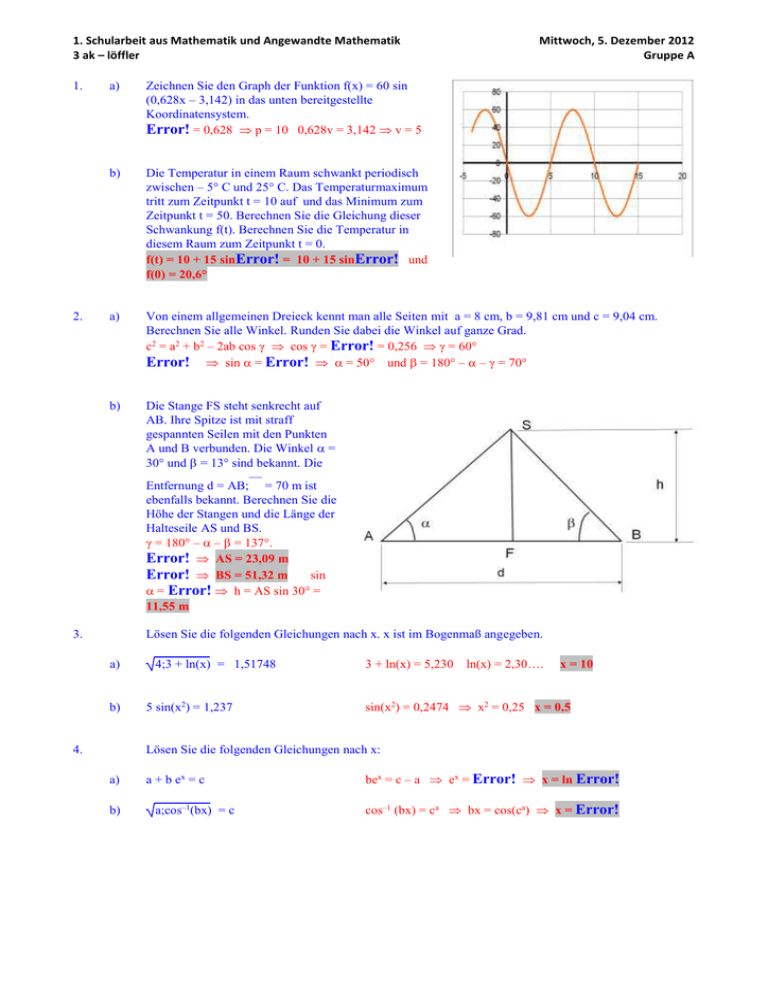
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 ak – löffler
1.
2.
Mittwoch, 5. Dezember 2012
Gruppe A
a)
Zeichnen Sie den Graph der Funktion f(x) = 60 sin
(0,628x – 3,142) in das unten bereitgestellte
Koordinatensystem.
Error! = 0,628  p = 10 0,628v = 3,142  v = 5
b)
Die Temperatur in einem Raum schwankt periodisch
zwischen – 5° C und 25° C. Das Temperaturmaximum
tritt zum Zeitpunkt t = 10 auf und das Minimum zum
Zeitpunkt t = 50. Berechnen Sie die Gleichung dieser
Schwankung f(t). Berechnen Sie die Temperatur in
diesem Raum zum Zeitpunkt t = 0.
f(t) = 10 + 15 sinError! = 10 + 15 sinError! und
f(0) = 20,6°
a)
Von einem allgemeinen Dreieck kennt man alle Seiten mit a = 8 cm, b = 9,81 cm und c = 9,04 cm.
Berechnen Sie alle Winkel. Runden Sie dabei die Winkel auf ganze Grad.
c2 = a2 + b2 – 2ab cos γ  cos γ = Error! = 0,256  γ = 60°
Error!  sin  = Error!   = 50° und  = 180° –  – γ = 70°
b)
Die Stange FS steht senkrecht auf
AB. Ihre Spitze ist mit straff
gespannten Seilen mit den Punkten
A und B verbunden. Die Winkel  =
30° und  = 13° sind bekannt. Die
––
Entfernung d = AB; = 70 m ist
ebenfalls bekannt. Berechnen Sie die
Höhe der Stangen und die Länge der
Halteseile AS und BS.
γ = 180° –  –  = 137°.
Error!  AS = 23,09 m
Error!  BS = 51,32 m sin
 = Error!  h = AS sin 30° =
11,55 m
3.
Lösen Sie die folgenden Gleichungen nach x. x ist im Bogenmaß angegeben.
a)
b)
4.
4;3 + ln(x) = 1,51748
5 sin(x2) = 1,237
3 + ln(x) = 5,230
ln(x) = 2,30….
x = 10
sin(x2) = 0,2474  x2 = 0,25 x = 0,5
Lösen Sie die folgenden Gleichungen nach x:
a)
b)
a + b ex = c
a;cos–1(bx) = c
bex = c – a  ex = Error!  x = ln Error!
cos–1 (bx) = ca  bx = cos(ca)  x = Error!
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 ak – löffler
1.
2.
Mittwoch, 5. Dezember 2012
Gruppe B
a)
Zeichnen Sie den Graph der Funktion f(x) = 60 sin
(0,628x – 3,142) in das unten bereitgestellte
Koordinatensystem.
Error! = 0,628  p = 10 0,628v = 3,142  v = 5
b)
Die Temperatur in einem Raum schwankt periodisch
zwischen – 5° C und 15° C. Das Temperaturmaximum
tritt zum Zeitpunkt t = 30 auf und das Minimum zum
Zeitpunkt t = 70. Berechnen Sie die Gleichung dieser
Schwankung f(t). Berechnen Sie die Temperatur in
diesem Raum zum Zeitpunkt t = 0.
f(t) = 5 + 10 sinError! und f(0) = –2,1°
a)
Von einem allgemeinen Dreieck kennt man alle Seiten mit a = 8 cm, b = 9,1 cm und c = 5,94 cm.
Berechnen Sie alle Winkel. Runden Sie dabei die Winkel auf ganze Grad.
c2 = a2 + b2 – 2ab cos γ  cos γ = Error!  γ = 40°
Error!  sin  = Error!   = 60° und  = 180° –  – γ = 80°
b)
Die Stange FS steht senkrecht auf
AB. Ihre Spitze ist mit straff
gespannten Seilen mit den Punkten
A und B verbunden. Die Winkel  =
30° und  = 15° sind bekannt. Die
––
Entfernung d = AB; = 70 m ist
ebenfalls bekannt. Berechnen Sie die
Höhe der Stangen und die Länge der
Halteseile AS und BS.
γ = 180° –  –  = 135°.
Error!  AS = 25,62 m
Error!  BS = 49,50 m sin
 = Error!  h = AS sin 30° =
12,81 m
3.
Lösen Sie die folgenden Gleichungen nach x. x ist im Bogenmaß angegeben.
a)
b)
4.
4;3 + ln(x) = 1,5648
5 sin(x2) = 2,353
3 + ln(x) = 5,995
ln(x) = 2,98….
x = 20
sin(x2) = 0,4706  x2 = 0,49  x = 0,7
Lösen Sie die folgenden Gleichungen nach x:
a)
b)
b ex – a = c
a;b cos–1(x) = c
bex = c + a  ex = Error!  x = ln Error!
b cos–1 (x) = ca  cos–1(x) = Error!  x = cos
Error!
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 ak – löffler
1.
2.
Mittwoch, 5. Dezember 2012
Gruppe A
a)
Zeichnen Sie den Graph der Funktion f(x) = 60 sin (0,628x – 3,142) in das unten
bereitgestellte Koordinatensystem.
b)
Die Temperatur in einem Raum schwankt periodisch zwischen – 5° C und 25° C.
Das Temperaturmaximum tritt zum Zeitpunkt t = 10 auf und das Minimum zum
Zeitpunkt t = 50.
Berechnen Sie die Gleichung dieser Schwankung f(t).
Berechnen Sie die Temperatur in diesem Raum zum Zeitpunkt t = 0.
a)
Von einem allgemeinen Dreieck kennt man alle Seiten mit
a = 8 cm, b = 9,81 cm und c = 9,04 cm.
Berechnen Sie alle Winkel. Runden Sie dabei die Winkel auf ganze Grad.
b)
Die Stange FS steht senkrecht
auf AB. Ihre Spitze ist mit
straff gespannten Seilen mit
den Punkten A und B
verbunden. Die Winkel  =
30° und  = 13° sind bekannt.
––
Die Entfernung d = AB; =
70 m ist ebenfalls bekannt.
Berechnen Sie die Höhe der
Stange und die Länge der
Halteseile AS und BS.
3.
Lösen Sie die folgenden Gleichungen nach x. x ist im Bogenmaß angegeben.
a)
b)
4.
4;3 + ln(x) = 1,51748
5 sin(x2) = 1,237
Lösen Sie die folgenden Gleichungen nach x:
a)
b)
a + b ex = c
a;cos–1(bx) = c
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 ak – löffler
1.
2.
Mittwoch, 5. Dezember 2012
Gruppe B
a)
Zeichnen Sie den Graph der Funktion f(x) = 60 sin (0,628x – 3,142) in das unten
bereitgestellte Koordinatensystem.
b)
Die Temperatur in einem Raum schwankt periodisch zwischen – 5° C und 15° C.
Das Temperaturmaximum tritt zum Zeitpunkt t = 30 auf und das Minimum zum
Zeitpunkt t = 70.
Berechnen Sie die Gleichung dieser Schwankung f(t).
Berechnen Sie die Temperatur in diesem Raum zum Zeitpunkt t = 0.
a)
Von einem allgemeinen Dreieck kennt man alle Seiten mit
a = 8 cm, b = 9,1 cm und c = 5,94 cm.
Berechnen Sie alle Winkel. Runden Sie dabei die Winkel auf ganze Grad.
b)
Die Stange FS steht senkrecht
auf AB. Ihre Spitze ist mit
straff gespannten Seilen mit
den Punkten A und B
verbunden. Die Winkel  =
30° und  = 15° sind bekannt.
––
Die Entfernung d = AB; =
70 m ist ebenfalls bekannt.
Berechnen Sie die Höhe der
Stangen und die Länge der
Halteseile AS und BS.
3.
Lösen Sie die folgenden Gleichungen nach x. x ist im Bogenmaß angegeben.
a)
b)
4.
4;3 + ln(x) = 1,5648
5 sin(x2) = 2,353
Lösen Sie die folgenden Gleichungen nach x:
a)
b)
b ex – a = c
a;b cos–1(x) = c