Selbstkontrolle Kapitel 2a Name: Konstruiere den Thaleskreis über
Werbung
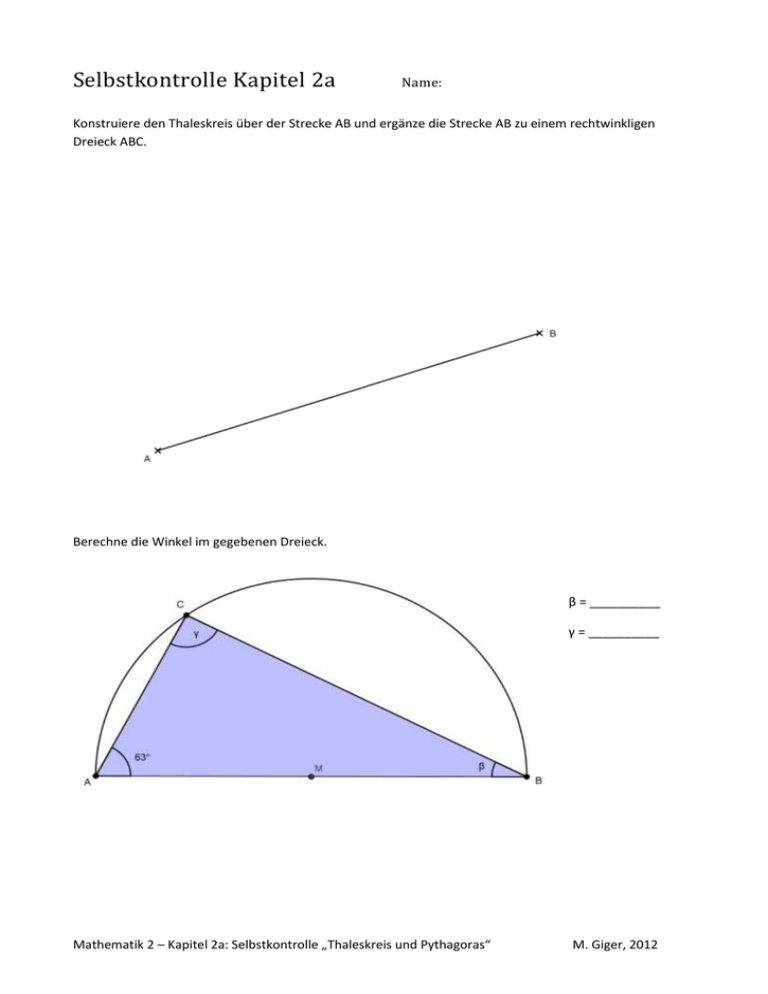
Selbstkontrolle Kapitel 2a Name: Konstruiere den Thaleskreis über der Strecke AB und ergänze die Strecke AB zu einem rechtwinkligen Dreieck ABC. Berechne die Winkel im gegebenen Dreieck. β = __________ γ = __________ Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Berechne die Winkel in den (Teil-)Dreiecken. β = __________ γ = __________ δ = __________ ε = __________ Berechne die Winkel in der gegeben Figur. α = __________ β = __________ γ = __________ δ = __________ Notiere den Satz des Pythagoras und forme ihn um. π 2 = ππ + ππ π2 = ππ − ππ π = √ππ + ππ π = √ππ − ππ Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Berechne die Längen der Diagonalen in der gegebenen Figur (alle Angaben in cm). Runde auf 2 Stellen nach dem Komma. Strecke AF: ______________________________ Strecke BI: _____________________________ Strecke AH: _____________________________ Strecke CE: _____________________________ Strecke AI: ______________________________ Strecke DI: _____________________________ Strecke BD: _____________________________ Strecke EG: _____________________________ Gegeben ist ein rechtwinkliges Dreieck mit den Seiten c = 18 m und b = 14.4 m. Gesucht ist die Kathete a. π = √ππ − ππ = √(ππ π)π + (ππ. π π)π = ππ. ππ Die Kathete a ist ____________________ lang. Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Gegeben ist ein rechtwinkliges Dreieck mit den Katheten a = 6 m und b = 3.2 m. Gesucht ist die Dreieckshöhe hc. Notiere alle verwendeten Formeln und Rechnungsschritte. Die Höhe des Dreiecks können wir mit Hilfe der Formel für die Dreiecksfläche berechnen: π΄= π ⋅ β π ⋅ π π ⋅ βπ = = 2 2 2 Durch Umformung erhalten wir: βπ = 2⋅π΄ 2⋅π΄ π⋅π = = π π π Wir können nun schrittweise rechnen: π = √π2 + π 2 = √(6π)2 + (3.2π)2 = 6.8π βπ = π ⋅ π 6π3.2π = = 2.824π π 6.8π Oder wir setzen c direkt in die umgeformte Flächenformel ein: βπ = π⋅π π⋅π 6π ⋅ 3.2π = = = 2.824π π √π2 + π 2 √(6π)2 + (3.2π)2 Die Höhe hc beträgt ____________________. Ergänze die Tabelle zum rechtwinkligen Dreieck (rechter Winkel bei γ, q = AH, p = HB). Rechne exakt. Seite a Seite b Seite c Strecke p Strecke q Höhe h Umfang U Fläche A 100 75 125 80 45 60 300 3750 128 96 160 102.4 57.6 76.8 384 6144 0.3 0.4 0.5 0.18 0.32 0.24 1.2 0.06 73.5 98 122.5 44.1 78.4 58.8 294 3601.5 48 64 80 28.8 51.2 38.4 192 1536 Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Selbstkontrolle Kapitel 2a Lösungsschlüssel Konstruiere den Thaleskreis über der Strecke AB und ergänze die Strecke AB zu einem rechtwinkligen Dreieck ABC. Berechne die Winkel im gegebenen Dreieck. β = 27° γ = 90° Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Berechne die Winkel in den (Teil-)Dreiecken. β = 29° γ = 90° δ = 29° ε = 61° Berechne die Winkel in der gegeben Figur. α = 68° β = 90° γ = 112° δ = 90° Notiere den Satz des Pythagoras und forme ihn um. π 2 = ππ + ππ π2 = ππ − ππ π = √ππ + ππ π = √ππ − ππ Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Berechne die Längen der Diagonalen in der gegebenen Figur (alle Angaben in cm). Runde auf 2 Stellen nach dem Komma. Strecke AF: 12.37 cm Strecke BI: 8.94 cm Strecke AH: 11.31 cm Strecke CE: 5 cm Strecke AI: 14.42 cm Strecke DI: 13 cm Strecke BD: 8.54 cm Strecke EG: 9.43 cm Gegeben ist ein rechtwinkliges Dreieck mit den Seiten c = 18 m und b = 14.4 m. Gesucht ist die Kathete a. π = √ππ − ππ = √(ππ π)π − (ππ. π π)π = ππ. π π Die Kathete a ist 10.8 m lang. Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012 Gegeben ist ein rechtwinkliges Dreieck mit den Katheten a = 6 m und b = 3.2 m. Gesucht ist die Dreieckshöhe hc. Notiere alle verwendeten Formeln und Rechnungsschritte. Die Höhe des Dreiecks können wir mit Hilfe der Formel für die Dreiecksfläche berechnen: π΄= π ⋅ β π ⋅ π π ⋅ βπ = = 2 2 2 Durch Umformung erhalten wir: βπ = 2⋅π΄ 2⋅π΄ π⋅π = = π π π Wir können nun schrittweise rechnen: π = √π2 + π 2 = √(6 π)2 + (3.2 π)2 = 6.8 π βπ = π ⋅ π 6 π β 3.2 π = = 2.824 π π 6.8 π Oder wir setzen c direkt in die umgeformte Flächenformel ein: βπ = π⋅π π⋅π 6 π ⋅ 3.2 π = = = 2.824 π π √π2 + π 2 √(6 π)2 + (3.2 π)2 Die Höhe hc beträgt 2.824 m. Ergänze die Tabelle zum rechtwinkligen Dreieck (rechter Winkel bei γ, q = AH, p = HB). Rechne exakt. Seite a Seite b Seite c Strecke p Strecke q Höhe h Umfang U Fläche A 100 75 125 80 45 60 300 3750 128 96 160 102.4 57.6 76.8 384 6144 0.3 0.4 0.5 0.18 0.32 0.24 1.2 0.06 73.5 98 122.5 44.1 78.4 58.8 294 3601.5 48 64 80 28.8 51.2 38.4 192 1536 Mathematik 2 – Kapitel 2a: Selbstkontrolle „Thaleskreis und Pythagoras“ M. Giger, 2012
