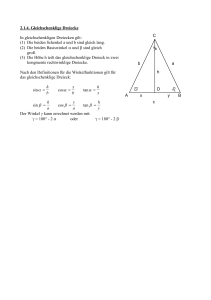
Gleichschenklige Dreiecke mit gegebenem A,P

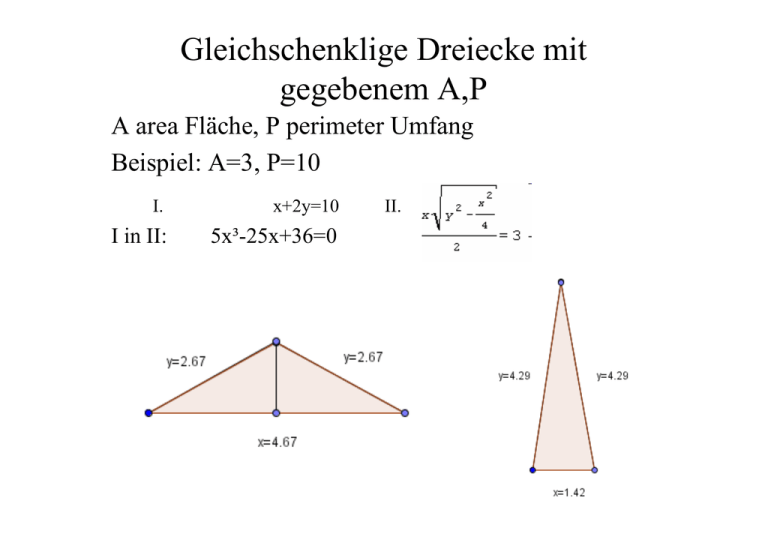
Gleichschenklige Dreiecke mit
gegebenem A,P
A area Fläche, P perimeter Umfang
Beispiel: A=3, P=10
I.
x+2y=10
I in II:
5x³-25x+36=0
II.
Lemma 1
Sei x die Basis eines gleichschenkligen
Dreiecks mit gegebener Fläche A und
gegebenem Umfang P, dann gilt:
2Px³-P²x²+16A²=0
(1)
Satz 2
Es gibt genau dann zwei verschiedene gleichschenklige Dreiecke mit Umfang P und Fläche
A,wenn
Es gibt genau ein gleichschenkliges Dreieck dann
und nur dann, wenn
Dieses Dreieck ist
gleichseitig.
Für die Scheitelwinkel Φ1 < Φ2 der beiden gleichschenkligen Dreiecke gilt stets Φ1 ≤ π/3 ≤ Φ2 .
f(x)=2Px³-P²x²+16A²
Graph von f für P=10 und A=3
Isoperimetrische Ungleichung für Dreiecke:
Es gilt stets:
P² ≥ 12√ 3 A
Corollar 3
Zu jedem nicht gleichseitigem Dreieck mit Fläche
A und Umfang P gibt es genau zwei gleichschenklige Dreiecke mit derselben Fläche und
demselben Umfang.
Newtons Parametrisierung
Ziel: x,y,z nur durch A, P und Φ (Winkel zwischen y und z)
darstellen
X>0
y.z existieren
+
>0
0
Satz 4
Es gibt genau dann ein Dreieck der Fläche A
mit Umfang P, Seiten x(Φ), y(Φ), z(Φ) wie
oben beschreiben, wenn die Bedingungen
s(Φ) > 0 und h(Φ) ≥ 0 erfüllt sind.
Das Dreieck ist genau dann gleichschenklig mit
Scheitelwinkel Φ, wenn h(Φ)=0.
Φ
Satz 5
In jedem nicht gleichseitigen Dreieck der Fläche A und Umfang
P erfüllt jeder Winkel Φ die Ungleichung Φ1 ≤ Φ ≤ Φ2, wobei
Φ1< π/3 < Φ2 die Scheitelwinkel der beiden gleichschenkligen
Dreiecke mit Fläche A und Umfang P bezeichnen.
Genauer:
wobei x1< P/3 < x2 die Basen der gleichschenkligen
Dreiecke sind.
Die Formel für den Scheitelwinkel folgt aus
x²=2y²-2y²cos(Φ) (Kosinussatz) und y=(P-x)/2
Bleibt zz:
Φ1 ≤ Φ ≤ Φ2
s(Φ) > 0 und h(Φ) ≥ 0
Heronsche Kurve
Geg: Dreieck mit A, P und
I.
II.
III.
8rPx³+4(r²-3r+1)P²x²-4(1-r)²P³x+(1-r)²P4+16(1+r)²A²=0
(2)
Ersetzt man x=P-y-x und
in (2) folgt:
P4-4P³(y+z)+4P²(y²+3yz+z²)-8Pyz(y+z)+16A²=0
z
y
Satz 6
In jedem nicht gleichseitigen Dreieck der Fläche A
und Umfang P erfüllt das Seitenverhältnis r von zwei
Seiten die Ungleichung r1 ≤ r ≤ r2 , r1<1< r2 und
r1r2=1, wobei r1und r2 die positiven NST von
32P4A²(2r6-3r4-3r²+2)-P8r²(r-1)²+6912A4r²(r+1)²=0 (3)‫‏‬
sind.