M echanik
Werbung

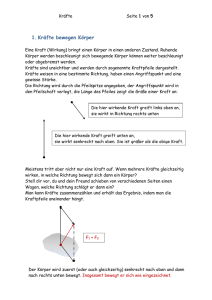
Mechanik E i n l e i t u n g Begriff Mechanik: Hebel, Wellrad (Lenkrad), Rolle, Flaschenzug, Schiefe Ebene, Rad. Vorteil dieser Maschinen: Arbeitserleichterung. Mit wenig Kraft kann man große Lasten bewegen oder große Kräfte erzeugen. Nachteil: Man muss längere Wege in Kauf nehmen. die Griechen bezeichneten diese einfachen Maschinen mit (Mechanä) übersetzt „kluger Einfall“. Das ist der Ursprung des Begriffs Mechanik. Kräfte Der Begriff Kraft stammt aus dem Indogermanischen „Grep“ und bedeutet „sich Krümmen“. Mit dem Krümmen der Muskeln kann ich Dinge, die ich vorhabe, umsetzen. Ich kann mit den Muskeln Wirkungen erzielen z.B.: Objekte verschieben; Ein Bild malen; Einen Stuhl werfen Beobachtet man solche Wirkungen, auch wenn sie nicht durch Muskelspiele hervorgerufen werden, dann sagt man „es ist eine Kraft am Werke“. 2 . K r a f t u n d R ü c k k r a f t Ich drücke mit der Hand gegen den Tisch, der Tisch drückt gleich stark zurück. Je fester ich drücke, desto fester drückt der Tisch zurück. Schleudert man aus einem Boot Steine in eine Richtung, dann setzt sich das Boot langsam in die Gegenrichtung in Bewegung. Kraftentstehung Bei der Kraftentstehung sind immer zwei Körper beteiligt. Übt ein Körper eine Kraft auf einen zweiten Körper aus, so wirkt der zweite Körper mit einer Rückkraft auf den ersten Körper zurück. Die beiden Kräfte sind gleich groß und wirken in entgegengesetzt Richtungen. Versuch 1 a. Wir führten Wasser durch einen Gummischlauch, an dessen Ende ein T-Röhrchen war. Das T-Röhrchen hatte an einem Ende einen Stopfen, so dass das Wasser an der einen Seite austrat, und das Rohr in die entgegengesetzte Richtung geknickt wurde. b. Als wir 1a wiederholten und den Stopfen im T-Röhrchen entfernten, verbog sich der Schlauch nicht. Versuch 2 Wir füllten Wasser in die Dose, welches durch die Röhrchen austrat und die Dose in Drehung versetzte. Versuch 3 Theresia und Marvin sitzen auf einer Schulbank. Thomas versucht die Bank wegzuschieben. Er drückt mit den Händen gegen die Schulbank und sucht sich Halt mit den Beinen am Boden (drückt gegen den Boden). Es gelingt ihm, die Bank wegzuschieben. Versuch 4 a. Wie Versuch 3, jedoch steht Thomas diesmal auf einem Skateboard. Beim Wegdrücken der Bank rollt das Skateboard nach hinten weg. b. Maximilian versucht auf einem Skateboard einen „unbelasteten“ Tisch wegzuschieben. Er schiebt den Tisch weg und rollt hinterher. Der Vorgang wiederholt sich. Versuch 5 Daniel und Merlin stellen sich auf Skateboards gegenüber und halten jeweils die Enden eines Seils in der Hand. Beide Ziehen am Seil. Sie rollen aufeinander zu. Versuch 6 a. In der Mitte steht Merlin auf einem Roller, rechts und links Daniel und H. auf zwei Skateboards. Merlin stößt die Herren auf den Skateboards gleichzeitig nach rechts und links gleich stark weg. Beide rollen weg und der Roller in der Mitte bleibt stehen. b. Die beiden rechts und links stoßen Merlin in der Mitte gleich stark an. Beide rollen weg und der Roller in der Mitte bleibt stehen. Zu Versuch 3 und 4: Kraft und Rückkraftpaare Die Länge der Kraftpfeile charakterisiert die Größe der Kraft. Kraft auf den Tisch: blaue Kraftpfeile Kraft auf den schiebenden: rote Kraftpfeile Kraft auf den Boden: grüne Kraftpfeile Wenn ich wissen will, was mit dem Schiebenden passiert, betrachte ich nur die Kräfte, die auf den Schiebenden wirken (rote Kraftpfeile). Die Bewegung ist immer in Richtung des größeren Pfeils (größere Kraft entsprechend beim Tisch). Versuch 5b Person 1 Person 2 Seil Person 2 zeiht Kraft auf Person 1: -> Seil bleibt in Ruhe Kraft auf Person 2: -> Kraft auf das Seil: -> zu Versuch 1 Wasser nach rechts -> T-Rohr nach links <- 3 . R u h e n d e K ö r p e r : K r a f t u n d G e g e n k r a f t 1. Mannschaft 2. Mannschaft Gegenkraft 2. Mannschaft Wand Weittragendes Prinzip: An einem ruhenden Körper muss zu jeder offensichtlich einwirkenden Kraft noch eine Gegenkraft auftreten, die entgegengesetzt und gleich große ist. F1 50 kp positiv F2 50kp negativ Ich ziehe am Tisch nach links. Bleibt der Tisch in Ruhe, dann bedeutet dies, dass der nach links wirkenden Kraft eine gleich große Kraft nach rechts entgegenwirkt (Gegenkraft). F 1 + F 2 = 50 kp + (- 50 kp) = 0 Versuch 7 Gewicht Latte Wir stellen ein Gewicht auf die Latte, welche sich daraufhin nach unten durchbog. Deutung: Fg Ich stelle das Gewicht auf die Latte. Die Schwerkraft biegt die Latte durch. Die Durchbiegung kommt zur Ruhe. Da die Latte in Ruhe ist, muss eine gleich große Kraft wie die Gewichtskraft nach oben wirken. Ff Fg Wir nehmen das Gewicht weg. Ff Die Formkraft lässt die Latte zurückspringen. Versuch 8 Wir hängten an eine Feder unterschiedliche Gewichte und maßen die Ausdehnung der Feder. Masse Gewichtskraft Ausdehnung 0,00 g 0,00 g 0 50,00 g 50,00 g 8,8 100,00 g 100,00 g 17,6 50,00 g 50,00 g 26,4 200,00 g 200,00 g 35,3 250,00 g 250,00 g 44,2 300,00 g 300,00 g 53,1 D = Gewichtskraft/Ausdehnung 50p/8,8 = 5,7 p/cm 100p/17,6 = 5,7 p/cm D ist die Federkonstante D=5,7 bedenkt, dass pro 5,7p die Feder um 1 cm ausgedehnt wird. Hook‘ sche Gesetz: Bei einer Feder verdoppelt sich bei doppelter Last die Ausdehnung, bei dreifacher Last ist die Ausdehnung dreimal so groß usw. Mit Hilfe des Hook‘ schen Gesetzes lässt sich die Kraftmessung auf eine Längenmessung reduzieren. Darauf beruhen die Federwaagen. 4 . K r a f t f o r t l e i t u n g Das Gemeinsame von Versuch 9 Zieht an einem Ende des Seils eine Kraft von n kp und wird das Seil festgehalten (z.B. durch eine Hand oder eine Gegengewicht) so dass es in Ruhe bleibt, dann erfährt jeder Punkt des Seils eine Spannungskraft von n kp. n kp n kp P n kp n kp Seile sind in der Lage eine Kraft an einen Anderen Ort fort zu leiten, ohne dass die Stärke der Kraft verändert wird. Über Rollen und ähnliches lässt sich aber die Richtung der Kraft verändern. Die Kraft wirkt immer in Richtung des Seiles. Das Gleiche gilt für Stangen und Balken. 5 . K r ä f t e g l e i c h g e w i c h t b e i m e h r e r e n K r ä f t e n 3 gleich große Kräfte greifen an einem Körper an. Wie müssen die Kräfte verteilt werden, damit der Körper in Ruhe bleibt? Wir vermuten 120° 120° 120° Versuch 10: 127° 143° 1kg 1kg 4kg 3kg 1kg 5kg Beim Loslassen verschiebt sich das System so lange, bis sich zwischen den Seile jeweils ein Winkel von 120° eingestellt hat. das System ist jetzt in Ruhe, die Kräfte gleichen sich aus. Das gleiche geschieht bei Versuch b mit anderen Gewischten, es stellt sich ein anderes Winkelverhältnis ein. 3 Kräfte zogen am Seildreipunkt. Das Seilsystem bewegt sich solange, bis die Kräfte sich ausgeglichen hat. Das Seilsystem kam zur Ruhe unter den oben gezeigten Bedingungen (siehe Lageplan zu 10a und 10b). Wir zeichnen zu Versuch 10a und b jeweils einen Kräfteplan. Wir zeichnen die wirkenden Kräfte als Pfeile maßstabs - und winkelgetreu ein. 120° 120° 120° 90° 127° 143° Kräfteaddition für ein System im Kräftegleichgewicht Hängen wir die Kraftpfeile aneinander, indem wir die Kraftpfeile parallel so verschieben, dass die Kraftpfeile im gleichen Sinne umlaufen (Einbahnverkehr), dann kehrt man zum Anfang zurück. Für den Fall des Gleichgewichts entsteht ein geschlossenes Kräftedreieck. Beispiel 1: Welche Winkel stellen sich ein? 2kg 2kg 86° 137° 137° 3kg Beispiel 2: Welche Kräfte wirken auf das Seil? Lageplan: 120° 2kg Kräfteplan: Ri t ch tu ng sk ra ft af kr s ng tu 60° 60° 4 cm ch Ri = 2 kp Beispiel 3: Dachkran Ric htu ng d er Kr aft au fB alk en 2 30° Richtung der Kraft auf Balken 1 Kr aft a uf 100 kp Ba lke n2 Kraft von/auf Balken 1 Das Kräftedreieck muss geschlossen sein. 6 . D i e R e s u l t i e r e n d e K r a f t d e r K r ä f t e a d d it i o n Beispiel A: Zwei Hafenschiffen schleppen einen Hochseetanker. Das eine Zieht mit 30 Tonnen (t), das andere mit 20 Tonnen Zugkraft. Der Winkel zwischen den Trossen (Seilen) beträgt 55°. Wie viel Tonnen gemeinsamer Zugkraft wird am Tanker wirksam und in welche Richtung wird er gezogen? Lageplan: 30t 55° 20t Kräfteplan: Maßstab 1cm ≙ 5t 6 cm = 20t 55° 20t FR = 45,5 t 9,9 cm 4 cm = 20t Die resultierende Kraft F R gibt die wirkende Kraft auf den Tanker an. Die resultierende Kraft der Kräftevereinigung (Kräfteaddition). Regel: Jeder Kraftanteil wird mit seinem Fuß an den Kopf des vorigen parallelverschoben hingelegt. Die resultierende (wirkende) Kraft ist dann der Kraftpfeil vom Fuß des ersten zum Kopf des letzten Pfeils. Beispiel B: Lageplan: 500kp 400kp 60° 90° 70° 300kp 700kp Kräfteplan: Maßstab 100 kp ≙ 1 cm 400 kp 60° 400 kp 70° 300 kp 700 kp Kinematik (Bewegungslehre) 1 . D i e g l e i c h f ö r m i g e B e w e g u n g In der gleichen Zeit einen gleich langen Weg. Zeit t Weg s Gesch. v = weg s/Zeit t nach 1s 2m v = 2m/1s = 2m/s nach 2s 4m v = 4m/2s = 2m/s nach 3s 6m v = 6m/3s = 2m/s Bei der gleichförmigen Bewegung bleibt die Geschwindigkeit gleich. Geschwindigkeit v = Weg s/ Zeit t Wichtige Einheiten der Geschwindigkeit 1km/h; 1m/s; 1Knoten = 1,852km/h 3,6km/h = 1m/s Berechnung von Geschwindigkeit v, Weg s oder Zeit t bei der gleichförmigen Bewegung v = s/t v x t = s t = s/v 2. Zusammengesetzte Bewegungen Beispiel: Ein Fährschiff überquert mit einer Geschwindigkeit von 4 m/s einen 60m breiten Fluss. Der Fluss hat eine Geschwindigkeit von 1m/s (nach rechts). Wie muss das Schiff fahren, damit es möglichst schnell auf der anderen Seite ist? Welchen Weg legt es dabei zurück und wie lange braucht es für die Überfahrt? 3. Gleichmäßig beschleunigte Bewegung Anfahrvorgang (Beschleunigung) beim Motorrad (Auto). Die Geschwindigkeitszunahme ist gleich. Gleichmäßig beschleunigte Bewegung aus der Ruhe. Zeit Geschwindigkeit Geschwindigkeitszunahme 0s 0 m/s 6m/s 2 1s 6 m/s 6m/s 2 2s 12 m/s 3s 18 m/s 4s 24 m/s Gesetze der gleichförmig beschleunigten Bewegung Beschleunigung a = Geschwindigkeitszunahme/Zeit Geschwindigkeitszunahme = Beschleunigung x Zeit zurückgelegter Weg s = 1/2 x a x t 2 Zeit t Geschwindigkeitszunahme Weg s=1/2 × a × t 2 1s 3m/s 2 × 1s = 3m/s 1/2 × 3m/s 2 × 1 2 s = 1,5 m 2s 3m/s 2 × 2s = 6m/s 1/2 × 3m/s 2 × 2 2 s = 6 m 3s 3m/s 2 × 3s = 9m/s 1/2 × 3m/s 2 × 3 2 s = 13,5 m 4s 3m/s 2 × 4s = 12m/s 1/2 × 3m/s 2 × 4 2 s = 24 m Wenn sich die Zeit verdoppelt, vervierfacht sich der Weg. Wenn sich die Zeit verdreifacht, verneunfacht sich der Weg. Wenn sich die Zeit vervierfacht, ist der Weg 16 mal so lang. Wenn sich die Zeit ver-n-facht, ver-n 2 -facht sich der Weg. gleichförmige Bewegung gleichmäßig beschleunigte Bewegung • Bewegung gleich schnell • Geschwindigkeit ist gleich • in der doppelten Zeit wird der doppelte Weg zurückgelegt • n-fache Zeit = n-facher Weg • Die Bewegung wird im gleichen Maß (linear) schneller (oder langsamer) • Beschleunigung beleibt gleich • n-fache Zeit = n 2 -facher Weg Freier Fall: Beschleunigung Zeit Geschwindigkeit Weg 1s 10m/s → 36 km/h 5m 2s 20m/s → 72 km/h 20m 3s 30m/s → 108 km/h 45m 4s 40m/s → 144 km/h 80m 5s 50m/s → 180 km/h 125m 6s 60m/s → 216 km/h 180m 7s 70m/s → 252 km/h 245m 8s 80m/s → 288 km/h 320m