Gleichmäßig beschleunigte Bewegung

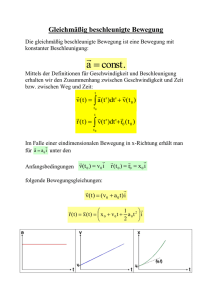
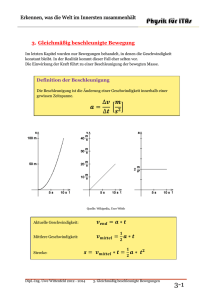
Gleichmäßig beschleunigte Bewegung
Die gleichmäßig beschleunigte Bewegung ist eine Bewegung mit
konstanter Beschleunigung:
r
a = const.
Mittels der Definitionen für Geschwindigkeit und Beschleunigung
erhalten wir den Zusammenhang zwischen Geschwindigkeit und Zeit
bzw. zwischen Weg und Zeit:
t
r
r
r
v( t ) = ∫ a ( t ' )dt ' + v( t 0 )
t0
t
r
r
r
r ( t ) = ∫ v( t ' )dt '+ r0 ( t 0 )
t0
Im Falle reiner eindimensionalen Bewegung in x-Richtung erhält man
r
für a = a 0 i unter den
r
r
v
(
t
)
v
=
Anfangsbedingungen
0
0i
r
r
r
r ( t 0 ) = r0 = x 0 i
folgende Bewegungsgleichungen:
r
r
v( t ) = ( v 0 + a 0 t ) i
r
r
1
r

r (t) = x(t) =  x 0 + v 0 t + a 0 t 2  i
2


Freier Fall
Der freie Fall ist eine gleichmäßig beschleunigte Bewegung unter
r dem
Einfluss der Erdbeschleunigung (Gravitationsbeschleunigung) g .
Die Erdbeschleunigung hängt vom Abstand zum Erdmittelpunkt ab,
ist jedoch für Bewegungen nahe der Erdoberfläche mit
r 
r
m r
g = gk =  − 9,81 2 k
s 

als konstant anzusehen. Dies gilt, solange für den zurückgelegten Weg
in Richtung der Erdbeschleunigung ∆z << R gilt (R-Erdradius).
Für einen Körper, der aus der Höhe h mit der Anfangsgeschwindigkeit
Null fällt, gelten dann folgende Gleichungen:
1
z = h − gt 2
2
v z = −gt
0
0
-5
-5
-10
-15
-20
-15
-25
-20
-30
-35
-25
-40
-30
-45
-35
-50
0
0,5
1
1,5
2
2,5
t/s
v(t)
z(t)-h
3
3,5
z-h / m
v / (m/s)
-10
Experiment zum freien Fall
h−z =
g 2
t
2
Freier Fall
2
t /s
0
0,05
0,1
2
0,15
0,2
140
0,25
140
120
120
h - z / cm
h-z = 496,97t
2
100
100
80
80
60
60
40
40
20
20
0
0
0
0,1
0,2
0,3
0,4
0,5
t/s
h-z(t)
h-z(t*t)
Linear (h-z(t*t))
Polynomisch (h-z(t))
Aus dem Anstieg m der linearisierten Darstellung h-z = f(t2) erhält
man
g
cm
m = ≈ 497 2
2
s
2
und damit g ≈ 9,9...m/s