GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION

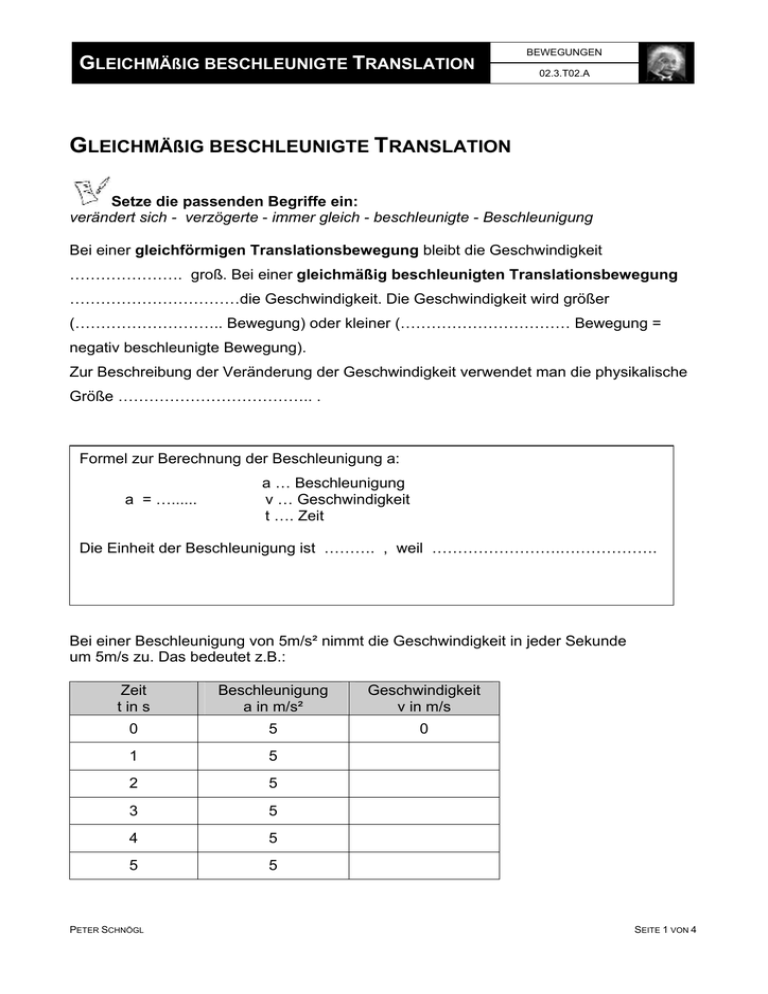
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
BEWEGUNGEN
02.3.T02.A
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
Setze die passenden Begriffe ein:
verändert sich - verzögerte - immer gleich - beschleunigte - Beschleunigung
Bei einer gleichförmigen Translationsbewegung bleibt die Geschwindigkeit
…………………. groß. Bei einer gleichmäßig beschleunigten Translationsbewegung
……………………………die Geschwindigkeit. Die Geschwindigkeit wird größer
(……………………….. Bewegung) oder kleiner (…………………………… Bewegung =
negativ beschleunigte Bewegung).
Zur Beschreibung der Veränderung der Geschwindigkeit verwendet man die physikalische
Größe ……………………………….. .
Formel zur Berechnung der Beschleunigung a:
a = …......
a … Beschleunigung
v … Geschwindigkeit
t …. Zeit
Die Einheit der Beschleunigung ist ………. , weil …………………….……………….
Bei einer Beschleunigung von 5m/s² nimmt die Geschwindigkeit in jeder Sekunde
um 5m/s zu. Das bedeutet z.B.:
Zeit
t in s
Beschleunigung
a in m/s²
Geschwindigkeit
v in m/s
0
5
0
1
5
2
5
3
5
4
5
5
5
PETER SCHNÖGL
SEITE 1 VON 4
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
BEWEGUNGEN
02.3.T02.A
Da sich die Geschwindigkeit laufend verändert, muss auch die Formel zur Berechnung des
Weges angepasst werden.
Formel zur Berechnung des zurückgelegten Weges s:
s = …......
s … Weg
a … Beschleunigung
t …. Zeit
Bei einer Beschleunigung von 3m/s² nimmt die Geschwindigkeit in jeder Sekunde
um ……………… zu. Das bedeutet z.B.:
Zeit
t in s
Beschleunigung
a in m/s²
Geschwindigkeit
v in m/s
Zurückgelegter Weg
s in m
0
3
0
0
1
3
2
3
3
3
4
3
5
3
Beispiel
Zwei Autos beschleunigen mit 3m/s² und 3,5m/s² jeweils von 0 auf 100km/h.
• Zeichne die Bewegungen (in 2 Farben) in ein Geschwindigkeits-Zeit-Diagramm ein.
• Zeichne die Bewegungen (in den gleichen 2 Farben) in ein Weg-Zeit-Diagramm ein.
Achtung: Die Achsen müssen skaliert (mit einer Skala versehen) werden!
v [m/s]
s [m]
t [s]
PETER SCHNÖGL
t [s]
SEITE 2 VON 4
BEWEGUNGEN
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
02.3.T02.A
Beschreibe den Verlauf der Geschwindigkeits-Zeit-Funktionen in Worten:
………………………………………………………………………………………………….....
………………………………………………………………………………………………….....
Beschreibe den Verlauf der Weg-Zeit-Funktionen in Worten:
………………………………………………………………………………………………….....
………………………………………………………………………………………………….....
GESAMMELTE FORMELN
Für die gleichmäßig beschleunigte Bewegung gelten folgende 3 Formeln:
a(t) = ……………
v(t) = ……………
s(t) = ……………
ZUSAMMENFASSUNG
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
Setze die passenden Begriffe ein:
Parabel - ändert sich nicht - ändert sich - ändert sich – gleichmäßig - lineare homogene
Gerade - eine Gerade – konstanten – quadratisch – Beschleunigung
Der Wert der Beschleunigungs-Zeit-Funktion ………………………. . Die Beschleunigung
besitzt einen ……………………….. Wert. Der Graph der Funktion ist ………………………. ,
parallel zur Zeit-Achse.
Der Wert der Geschwindigkeits-Zeit-Funktion …………………… . Die Geschwindigkeit
nimmt …………………………… zu. Der Graph der Funktion ist eine
………………………………… . Die Steigung der Geschwindigkeits-Zeit-Funktion gibt die
…………………………………. an.
Der Wert der Weg-Zeit-Funktion ……………………… . Der Weg nimmt ……………..……
mit der Zeit zu. Der Graph der Funktion ist eine ………………………. .
PETER SCHNÖGL
SEITE 3 VON 4
GLEICHMÄßIG BESCHLEUNIGTE TRANSLATION
BEWEGUNGEN
02.3.T02.A
SPEZIALFALL - FREIER FALL
Setze die passenden Begriffe ein:
ändert sich nicht – gleichmäßig – Fallbeschleunigung – quadratisch – beschleunigte –
g=9,81m/s² – Standort
Der freie Fall ist ebenfalls eine ……………………………….. Bewegung. Der fallende
Körper wird von der Erde mit der ………………………………. (auch genannt Gravitationsbeschleunigung) angezogen. Diese besitzt im Mittel einen Wert von ……………………… .
Der Wert der Fallbeschleunigung g ………………….……………. . Dieser Wert hängt vom
…………………. ab (am Äquator hat g einen Wert von g=9,76m/s² und am Pol =9,87m/s²).
Die Geschwindigkeit nimmt ……………………………. zu.
Der Wert der Weg-Zeit-Funktion nimmt ……………..…… mit der Zeit zu.
Löse die folgenden Beispiele:
1.
Ein Dachziegel fällt aus einer Höhe von 10m auf den Gehsteig. Wie lange fällt er?
Mit welcher Geschwindigkeit kommt er unten an?
2.
Ein voll beladener Jumbo-Jet beschleunigt mit 1,6m/s². Nach welcher Zeit hat er die
1km lange Startbahn zurückgelegt? Wie schnell ist er zu dieser Zeit?
3.
Ein Lastenzug fährt mit einer Geschwindigkeit von 108km/h. Er bremst bei einer
Vollbremsung mit 0,4m/s². Wie lange benötigt er um stehen zu bleiben und wie groß
ist sein Bremsweg?
(3: 75s , 1,125km / 2: 35s , 203km/h / 1: 1,4s , 50km/h)
PETER SCHNÖGL
SEITE 4 VON 4