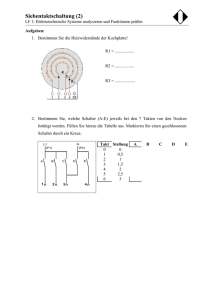
Wenn 2 widerstände parallel geschaltet sind, gilt folgende Formel:
Werbung

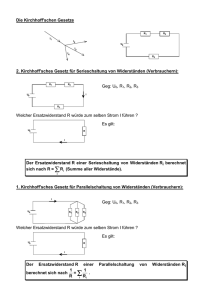
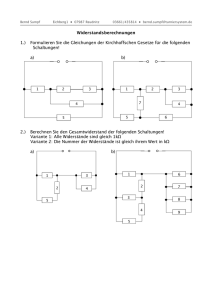
Parallelschaltung von Widerständen Wenn Widerstände parallel geschaltet sind, läßt sich der gesamte Widerstand bekanntlich in allen Fällen nach folgender Formel berechnen, ganz gleich wieviel es sind und welchen Wert die einzelnen Widerstände haben. 1/Rges = 1/R1+1/R2+1/R3+1/Rn+1/Rn+1 Dabei nicht zu vergessen ist, den Kehrwert von 1/R zu berechnen, um R ges zu haben, was im Grunde ehe derart passend wäre: Rges = 1/[1/R1+1/R2+1/R3+1/Rn+1/Rn+1] Sollten sämtliche „n“ Widerstände denselben Wert haben, wird es mit folgender Formel vereinfacht: Rges = R1/n Wenn aber nur 2 Widerstände R1 und R2 zueinander parallel geschaltet sind, wird der Ersatzwiderstand R12 wie folgt errechnet. R12 = (R1.R2)/(R1+R2) Sind zwei Widerstände R2 und R3 in Reihe und dabei zusammen parallel zu R1 geschaltet, läßt sich die Formel erweitern. R123a = R1.(R2+R3)/(R1+R2+R3) Wenn dagegen zwei Widerstände R2 und R3 zueinander parallel und dabei zusammen in Reihe zu R1 geschaltet sind, sieht die Formel dann anders aus. R123b = R1+ (R2.R3)/R2+R3) In einem Netzwerk von Widerständen ist die eine Formel (mit Vorsicht) je nach Konfiguration und Kombination entsprechend auszuwählen, wobei die erste immer grundlegend bleibt, allerdings anhand der Formeln für erweiterte Parallelschaltungen, wobei erstmals zwei Alternativen nach dem Verfahren für R123a oder für R123b zur Verfügung stehen. Folgendes Netzwerk (in diesem einzelnen Fall) gibt mir Anlaß nachzuforschen, wie das Problem anders zu lösen. Sobald Rges (in Ohm) errechnet ist, kann dann der lieferte Strom (in A) von der Betriebsspannung (in V) ermittelt werden, bekanntlich nach folgender Formel: U = RI <=> I = U/R Sobald die Stromstärke ermittelt ist, läßt sind dann die Stromstärke je nach Verzweigungen in der Leitung ermitteln und darüber hinaus jede Spannung, die auf den einzelnen Widerständen abfallen. A] Alternative 1 Erstmals mit dem ersten Verfahren nach R123a, wäre es offensichtlich leichter aber nicht unbedingt schneller. • • Der Ersatzwiderstand von R7 wird Rges1 bezeichnet Der Ersatzwiderstand von R8 wird Rges2 bezeichnet Es spielt zwar keine Rolle, ob Rges1 zuerst berechnet wird, also von links nach rechts, oder Rges2 von rechts nach links. Die Reihenfolge ist aber immerhin zu berücksichtigen, vor allem im Falle mehrerer Parallelschaltungen, mit der Folge daß Gleichungen ineinander verschaltet sind. 1 Schritt: Rges1 = [R7.(R3+R8+R4)]/(R7+R3+R8+R4) = [R7.(R3+Rges2+R4)]/(R7+R3+Rges2+R4) 2. Schritt: Rges2 = [R8.(R5+R9+R6)]/(R8+R5+R9+R6) 3. Schritt: Rges = R1 + R2 + Rges1 = R1 + R2 + [R7.(R3+Rges2+R4)]/(R7+R3+Rges2+R4) Wie man im 3 Schritt sieht, wäre es rückwärts, also von rechts nach links eher leichter, d.h. erst Rges2 berechnen und danach Rges1, ehe man zum Endergebnis kommt. Wenn alle Widerstände zueinander unterschiedlich sind, gibt es meines Wissens kein anderes Verfahren, welches etwa umständlich ist. Es geht aber noch schneller, sollten alle Widerstände im Netzwerk miteinander gleich sein, z.B. mit 1 Ω oder 1 kΩ. Rges2 = [R8.(R5+R9+R6)]/(R8+R5+R9+R6) = [1.(1+1+1)]/(1+1+1+1) = 3/4 kΩ. Rges1 = [R7.(R3+Rges2+R4)]/(R7+R3+Rges2+R4) = [1.(1+3/4+1)]/(1+1+3/4+1) = (11/4)/(15/4) = 11/15 kΩ. Dann komme ich dazu, weitere Formeln zu schreiben, um ans Endergebnis schneller zu gelangen. Rges2 = [1.(1+1+1)]/(1+1+1+1) = R.3R/4R = 3R/4 Rges1 = [1.(1+3/4+1)]/(1+1+3/4+1) = [R.(2R+3R/4)]/(3R+3R/4) = R.(8R+3R)/(12R+3R) = 11R/15 Somit ist Rges = 2R + 11R/15 = 41R/15 kΩ ≈ 2,73 kΩ Er ergibt sich folgende Gleichung bzw. Reihenfolgen mit x als Zähler und y als Nenner, um jeweils für jede Parallelschaltung das Verhältnis zu berechnen. R(n+1) = x(n+1)/y(n+1) = (xn+2yn)/(xn+3yn) Der Einfachheit wegen schreibe ich von nun an folgendermaßen: Rges = X2/Y2 <=> Rges = (X+2Y)/(X+3Y) Dies gilt nur für den Ersatzwiderstand an beliebiger parallelen Schaltung, nur dann wenn das Verhältnis von X1/Y1 bekannt ist. Ansonsten sollte man mit X1 = 1 und Y1 = 1 beginnen! Am Ende sollte es dabei nicht vergessen, noch die ersten 2 Widerstände R1 und R2 dazu zu addieren, die sich in der Reihe neben der Betriebsspannung befinden. Rges = [(2X+6Y)+(X+2Y)]/(X+3Y) <=> Rges =(3X+7Y)/(X+3Y) Der Reihe nach ergibt es sich dann folgende Verhältnisse: X/Y: 1/1 R (keine // Schaltung) ; 3/4 R; 11/15 R; 41/56 R; 153/209 R; 571/780 R; 2131/2911 R Wie dies sofort auffällt, wird es zwar immer niederohmiger, je mehr Parallelschaltungen es gibt, aber anscheinend am Ende mit einer Sättigung, so daß Werte zwischen nur 75% und 73% relativ gering und belanglos anzusehen wären. => 1.R; 0,750.R; 0,733 333.R; 0,732 142 857.R; 0,732 057 416.R; 0,732 051 282.R; 0,732 050 842.R Da es keine Sinn hat, alles auswendig zu lernen, genügt es also, einfach die obige Gleichung zu verwenden und so weiter für jede erweiterte Parallelschaltung mit gleichen Werten von Widerständen in derselben Konfiguration vorzugehen. Folgende Gleichungen sind dabei (zum Forschungszweck) interessant: • • • • • X2 = Y2-Y1 Y2 = (X3-X2)/2 X1 = Y2-3Y1 X4 = 1+4(X3-X1) Y4 = X4+Y3 B] Alternative 2 Ansonsten mit dem zweiten Verfahren nach R123b wäre es offensichtlich zwar noch schneller aber unübersichtlicher, denn ich betrachte R1 und R2 als einziger Widerstand R12 und ebenfalls R3 und R4 dann als R3, da sie zueinander in der Reihe geschaltet sind. • • Der Ersatzwiderstand von R12 wird nun Rges1 bezeichnet Der Ersatzwiderstand von R34 wird nun Rges2 bezeichnet Rges2 = R34+[R8.(R56+R9)]/(R8+R56+R9) = 2+[1.(2+1)]/(1+2+1) = 2 + 3/4 = 11/4 kΩ Rges1 = R12+[[R7.(R34+R8)]/(R7+R34+R8)] = R12+[(R7.Rges2)/(R7+ Rges2)] = 2+[(1.11/4)]/(1+11/4) = 2+[(11/4)]/(15/4) = 2+11/15 = 41/15 kΩ ≈ 2,73 kΩ Im Vergleich zu der 1. Alternative stimmt das Endergebnis überein. Nun komme ich dazu, auch hier weitere Formeln zu schreiben, um aufs Endergebnis hoffentlich noch schneller zu kommen, jedoch diesmal mit den ersten zwei Widerständen R1 und R2 zusammen, um nachfolgende Verhältnisse zu erzielen. Im Vergleich zur ersten Alternativen werden die Zähler jeweils zum vorherigen Bruch (nach links) verschoben. X/Y: 3/1 R(keine // Schaltung) ; 11/4.R; 41/15 R; 153/56 R; 571/209 R; 2131/780 R; 7953/2911 R Abgeleitet ergibt sich: Y2 = X1 + Y1 X2 = X1+2Y2 Y2 = (X2-X1)/2 Es folgt daraus: X2/Y2 = (3X1+2Y1)/(X1+Y1) => R(n+1) = (3xn+2yn)/(xn+yn) Soweit X/Y bekannt wird, ist es kein Problem, das Nächste zu berechnen. Ansonsten ist am Anfang ohne Parallelschaltung mit dem Verhältnis X0/Y0 = 3/1 zu beginnen, da bereits 3 Widerstände vorliegen. C] Abschluß: Nach Vergleich beider Alternativen wäre es meines Erachtens eher die erste vorzuziehen, da die Formel mit 1/1 zu Beginn leichter ist, sich zu merken, und dabei Parallelschaltungen übersichtlich ohne Fehler besser zurück verfolgt werden können, allerdings mit einem kleinen Unterschied, der zu beachten ist, nämlich ob noch zu errechnende Widerstände übrig bleiben. Nachfolgend immerhin als Abhilfe, sofern das letzte Verhältnis nach allen durchgelaufenen Parallelschaltungen ermittelt ist, kommt es letztlich zur Formel „restlos“ für den gesamten Widerstand: Für 1. Alternative R(n+1) = (xn+2yn)/(xn+3yn) mit x0/y0 = 1/1 zu Beginn Rges = (3X+7Y)/(X+3Y) Für 2. Alternative R(n+1) = (3xn+2yn)/(xn+yn) mit x0/y0 = 3/1 zu Beginn Rges = (3X+2Y)/(X+Y) Wenn Widerstände im Netzwerk unterschiedliche Werte haben, müssen wieder einzelne Schritte für jeden Widerstand befolgt werden. Martial Jardon (24.02.13)