Document

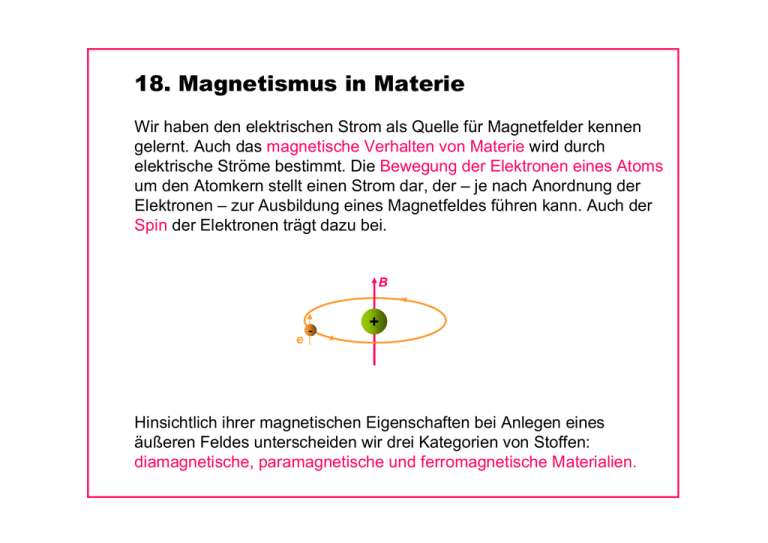
18. Magnetismus in Materie
Wir haben den elektrischen Strom als Quelle für Magnetfelder kennen
gelernt. Auch das magnetische Verhalten von Materie wird durch
elektrische Ströme bestimmt. Die Bewegung der Elektronen eines Atoms
um den Atomkern stellt einen Strom dar, der – je nach Anordnung der
Elektronen – zur Ausbildung eines Magnetfeldes führen kann. Auch der
Spin der Elektronen trägt dazu bei.
B
e
-
+
Hinsichtlich ihrer magnetischen Eigenschaften bei Anlegen eines
äußeren Feldes unterscheiden wir drei Kategorien von Stoffen:
diamagnetische, paramagnetische und ferromagnetische Materialien.
Diamagnetische Stoffe
Die Atome diamagnetischer Stoffe besitzen kein permanentes
magnetisches Moment. Bringt man diamagnetische Stoffe in ein äußeres
Magnetfeld, so wird die Bewegung der Elektronen gestört. Dies führt zur
Ausbildung eines entgegen gerichteten magnetischen Momentes, das zu
einer Abschwächung des äußeren Feldes führt.
Paramagnetische Stoffe
Die Atome paramagnetischer Stoffe besitzen ein permanentes
magnetisches Moment. Durch Anlegen eines äußeren Magnetfeldes
kommt es zu einer teilweisen Ausrichtung der Atome, wodurch das
äußere Feld leicht verstärkt wird.
Zur Beschreibung der magnetischen Eigenschaften führt man eine neue
Materialkonstante ein, die Permeabilität μ. Sie beschreibt, um wieviel
sich das Magnetfeld in Anwesenheit des Stoffes gegenüber im Vakuum
erhöht.
B = μ ⋅ B0
Für diamagnetische Stoffe ist μ kleiner eins, für paramagnetische größer
eins.
Ferromagnetische Stoffe
Auch in ferromagnetischen Stoffen besitzen die Atome ein permanentes
magnetisches Moment. Sie haben aber die Besonderheit, dass die
Momente der einzelnen Atome sich spontan gemeinsam ausrichten
können. Daher kommt es auch ohne Anlegen eines äußeren Feldes zur
Ausbildung so genannter Weisscher Bezirke, innerhalb derer viele
tausend Atome gleich ausgerichtet sind.
Durch Anlegen eines Magnetfeldes richten
sich die Weisschen Bezirke nach dem
äußeren Feld aus, wodurch dieses enorm
verstärkt wird. Die Permeabilitäten
ferromagnetischer Stoffe können 104-105
betragen.
Dadurch kann z.B. das Magnetfeld einer
stromdurchflossenen Spule erheblich erhöht werden, wenn die Spule um
einen Eisenkern gewickelt ist.
Nach Entfernen des äußeren Magnetfeldes
können ferromagnetische Stoffe ihre Magnetisierung beibehalten. Man
spricht dann von Remanenz.
19. Induktion
Wir haben gesehen, dass ein elektrischer Strom ein Magnetfeld erzeugt.
In diesem Kapitel werden wir sehen, dass das umgekehrte ebenso
möglich ist: ein Magnetfeld kann in einem Leiter einen elektrischen
Strom erzeugen. Entscheidend für das Verständnis dieses Phänomens
ist das Konzept des magnetischen Flusses.
19.1 Der magnetische Fluss
Unter dem magnetischen Fluss Φ verstehen wir das Produkt aus dem
mittleren Magnetfeld B, das durch eine Fläche A tritt, wobei nur die
Komponente senkrecht zu A relevant ist. Ist B über die gesamte Fläche
konstant und senkrecht zu A, so ergibt sich einfach:
Φ = B⋅A
B
Andernfalls gilt allgemein:
Φ = ∫ B ⋅ dA
A
A
Einheit des magnetischen Flusses ist das Weber: 1 Wb = 1 Tm2 = 1 Vs
19.2 Faradaysches Gesetz
Wird eine Leiterschleife in ein Magnetfeld hinein oder hinaus bewegt, so
wird in der Leiterschleife eine Spannung induziert.
Entscheidend hierfür ist, dass der magnetische Fluss durch die von der
Leiterschleife geformte Fläche verändert wird.
Dies wird durch das Faradaysche
Induktionsgesetz beschrieben:
B
dΦ
dt
Für eine einfache Leiterschleife ist n = 1. Nimmt man stattdessen eine
Spule mit n Windungen, so tritt der Fluss n-mal durch die Fläche der
Spule. Eine Änderung des Flusses ergibt sich, wenn
U ind = −n
•
•
•
•
die Stärke des Magnetfeldes B verändert wird
die Fläche A verändert wird
die Orientierung von A zu B verändert wird
die Leiterschleife durch Bereiche verschiedener Feldstärke bewegt
wird
19.3 Die Lenzsche Regel
Wenn eine Spannung in einer Leiterschleife induziert wird, so fließt ein
Strom. Dieser Strom erzeugt natürlich seinerseits ein Magnetfeld. Dabei
ist die Richtung des Stroms so, dass der dadurch entstehende
magnetische Fluss entgegen der Flussänderung, die die Spannung
induziert hat, gerichtet ist. Dies ist der Inhalt der Lenzschen Regel:
Die Induktionsspannung und der Strom, den sie hervorruft, sind stets so
gerichtet, dass sie ihrer Ursache entgegenwirken.
Dies wird durch das Minuszeichen im Faradayschen Induktionsgesetz
zum Ausdruck gebracht:
U ind = −n
dΦ
dt
19.4 Induktivität
Wie wir gesehen haben, erzeugt eine stromdurchflossene Spule ein
Magnetfeld der Stärke
B = μ0
n
I
l
Wir wollen nun den magnetischen Fluss durch die Spule berechnen.
Dafür nehmen wir an, dass das Magnetfeld homogen ist und senkrecht
zur Querschnittsfläche A der Spule steht. Für eine lange, eng gewickelte
Spule ist das eine gute Näherung. Für den magnetischen Fluss gilt
n2
Φ = nBA = μ0
A ⋅I = L ⋅I
l
Die Größe L heißt Selbstinduktivität oder einfach Induktivität der Spule:
n2
L = μ0
A
l
Die Einheit der Induktivität ist das Henry (H): 1 H = 1 Wb / A
Für den magnetischen Fluss durch die Spule gilt also:
Φ = L ⋅I
Falls sich der Strom ändert, ändert sich demnach auch der magnetische
Fluss durch die Spule. Da L eine Konstante ist, erhalten wir:
dΦ
dI
= L⋅
dt
dt
Nach dem Faradayschen Induktionsgesetz induziert die Flussänderung
eine Spannung Uind in der Spule:
U ind = −
dΦ
dI
= −L
dt
dt
Die induzierte Spannung ist also umso größer, je schneller sich die
Stromstärke ändert, und nach der Lenzschen Regel ist sie Ihrer
Ursache, also der Stromänderung, entgegen gerichtet. Die
Selbstinduktivität einer Spule (eines Stromkreises) verhindert also, dass
sich die Stromstärke sprunghaft ändert.
19.5 Die Erzeugung von Wechselstrom
Zur Erzeugung von Wechselströmen verwendet man elektrische
Generatoren. Diese funktionieren
U
nach folgendem Prinzip:
Eine Leiterschleife der Fläche A
rotiert mit der Winkelgeschwindigkeit
ω in einem Magnetfeld B.
Dies bewirkt eine periodische Änderung
des Flusses Φ durch die Schleife:
α
Φ (t ) = A ⋅ B = AB cos α = AB cos ωt
Nach dem Induktionsgesetz wird eine sinusförmige Spannung U in der
Schleife induziert:
U (t ) = −
dΦ
= ABω sin ωt = U0 sin ωt
dt
Für die Wechselspannung aus dem Netz gilt ν = ω/2π = 50 Hz.
Fällt eine Wechselspannung an einem ohmschen Widerstand ab, so
fließt ein Wechselstrom.
Der durch einen ohmschen Widerstand
fließende Strom ist mit der
Wechselspannung in Phase, d.h. beide
nehmen zu gleichen Zeitpunkten ihre
Extremwerte an.
I
+
U
−
R
Für den Wechselstrom gilt:
I (t ) =
U0
sin ωt = I0 sin ωt
R
Die Leistung, die im Widerstand in Wärme umgesetzt wird, ist ebenfalls
eine Funktion der Zeit:
P (t ) = I 2 R = I02 R sin2 ωt
Beachten Sie, dass die Leistung stets positiv (oder null) ist. Für die
mittlere Leistung gilt:
1
P = I02 R
2
Effektivwerte
Wie wir gesehen haben, ändern sich Stromstärke und Spannung
periodisch mit der Zeit. Technisch interessant sind aber zeitliche
Mittelwerte. Man definiert den Effektivwert des Wechselstroms als
diejenige Stromstärke, die ein Gleichstrom haben müsste, um die
gleiche mittlere Leistung zu erbringen.
2
P = Ieff
R=
I
1 2
I0 R ⇒ Ieff = 0
2
2
Analog ergibt sich der Effektivwert der Wechselspannung:
Ueff =
U0
2
Die Angabe der Netzspannung von 230 V bezieht sich auf den
Effektivwert. Der Maximalwert beträgt demnach
U0,Netz = 2 ⋅ 230 V = 325 V
19.6 Transformator
Ein Transformator dient dazu, einen
Wechselstrom der Spannung U1 in
einen Wechselstrom der Spannung U2
umzuwandeln.
U1
U2
n1
n2
Dazu wickelt man eine Primärspule mit n1 Windungen, an der U1
anliegt, um einen Eisenkern. Um den gleichen Eisenkern wickelt man die
Sekundärspule mit n2 Windungen, an der die transformierte Spannung
U2 abgegriffen wird.
Die Wechselspannung U1 bewirkt eine periodische Flussänderung durch
die Primärspule. Über den Eisenkern wird die Flussänderung auf die
Sekundärspule übertragen, in der dann wiederum eine
Wechselspannung U2 induziert wird. Nach dem Induktionsgesetz gilt:
U1 = n1
dΦ
dΦ
n
bzw. U2 = n2
⇒ U2 = 2 U1
dt
dt
n1