Hausaufgaben vom 17.10.2012

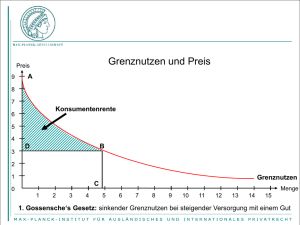
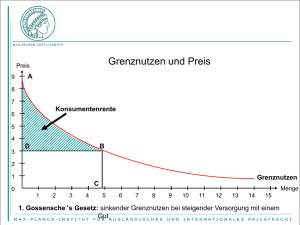
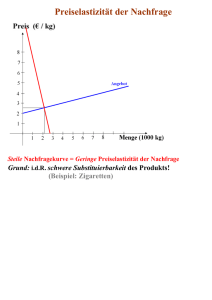
Musterlösung 5
Ökonomie
HS 12
Hausaufgaben vom 17.10.2012
1. Ein Monopolbetrieb ist durch einen Erlös von E(x)=-x(x-60) und Gesamtkosten K(x)=30x+100
gekennzeichnet. Bei welcher Stückzahl erreicht der Betrieb den grössten Gewinn? Bei welchen
fixen Kosten würde er im Gewinnmaximum weder mit Gewinn noch mit Verlust arbeiten?
Auch für ein monopolistisches Unternehmen gilt, dass der Gewinn maximiert werden soll. Das
Gewinnmaximum ist dort, wo die Ableitung des Gewinns null ist.
( )
( )
( )
Der Grenzerlös E‘(x) kann mit den Grenzkosten K‘(x) gleichgesetzt werden.
( )
( )
( )
( )
( )
( )
Bei einer Stückzahl von 15 erreicht der Betrieb den grössten Gewinn.
In der Kostenfunktion K(x) können die bisherigen fixen und variablen Kosten abgelesen werden.
( )
Variable Kosten = 30x (abhängig von der produzierten Menge)
Fixe Kosten = 100 (fallen auch an, wenn nichts produziert wird)
Gewinn bei x=15 (Gewinnmaximum): (
[
)
(
)]
[
]
Bei fixen Kosten von 100+125=225 würde der Betrieb im Gewinnmaximum weder mit Gewinn noch
mit Verlust arbeiten.
2. Henry, Bea und Romy betreiben die einzige Kneipe in einer Stadt. H will so viele Drinks wie
möglich ohne Verlust verkaufen. B möchte so viel Erlös wie möglich erzielen. R möchte den
maximalen Profit realisieren. Welche Preis-Mengen-Kombinationen entsprechen diesen drei
Strategien? Erläutern und begründen Sie ihre Antworten anhand von Grafiken.
Henry: Damit möglichst viel verkauft werden kann und kein Verlust entsteht, d.h. G(x)=0, muss der
Preis gerade die Durchschnittskosten decken.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
( )
Musterlösung 5
Bea:
Ökonomie
HS 12
Der Erlös ist in der Grafik gegeben durch die Fläche unter der Grenzerlöskurve. Um möglichst
viel Erlös zu erzielen, muss der Grenzerlös E‘(x)=0 sein. Grafisch ist dies bei der Menge
der
Fall.
Romy: Analog Aufgabe 1 gilt: Grenzerlös = Grenzkosten
E‘(xR) = K‘(xR)
Nachdem die Menge xR bestimmt wurde, wird der entsprechende Preis über die
Nachfragekurve definiert. Diesen Punkt nennt man Cournot-Punkt.
P
Grenzkosten
Grenzerlös
Totale Durchschnittskosten
Romy
Henry
Bea
Nachfrage
xR
xH
xB
x
3. Ein Pharmaunternehmen hat ein neues Medikament entwickelt. Das Unternehmen hat ein
Patent auf dieses Medikament bekommen und ist daher einziger Anbieter dieses Medikaments.
Die Herstellungskosten sind gegeben durch K(x) = 20x. Das Unternehmen nimmt folgende
Nachfragefunktion an: x = 100 – ½ p. Berechnen Sie den Preis und die angebotene Menge im
Gleichgewicht.
Der Gewinn lässt sich folgendermassen berechnen:
( )
( )
( )
( )
( )
Der Preis in Abhängigkeit von x ergibt sich aus der Nachfragefunktion:
( )
Das Gewinnmaximum ergibt sich bei der Bedingung:
( )
( )
( )
( )
( )
(
)
( )
( )
2
Musterlösung 5
Ökonomie
HS 12

x = 45
Die angebotene Menge liegt bei 45.
Um den Preis im Cournot-Punkt zu bestimmen, setzen wir diesen Wert in die Nachfragefunktion ein.
(
)
Bei einem Monopol liegt der Preis bei 110.
4. Die Firma SAP entwickelt einen neuen Chip, auf den sie sofort ein Patent erhält.
a) Zeichnen Sie ein Diagramm, das Produzentenrente, Konsumentenrente und
Gesamtrente für den Markt des neuen Chips zeigt.
b) Wie ändern sich die Grössen aus a., wenn SAP vollständige Preisdifferenzierung machen
kann, d.h. die unterschiedliche Zahlungsbereitschaft der Nachfrager adäquat
berücksichtigt?
a) Die Firma SAP ist in einer Monopolsituation für diesen Chip aufgrund des Patents.
P
Konsumentenrente
Produzentenrente
Cournot-Punkt
Grenzkosten
Nachfrage
Grenzerlös
x
Die Gesamtrente ergibt sich aus der Addition der Konsumentenrente und der Produzentenrente.
b) Vollständige Preisdifferenzierung bedeutet, dass die Firma SAP ihr Produkt an verschiedene
Kunden zu unterschiedlichen Preisen verkauft. Der Anbieter bietet das Produkt dabei zu dem Preis
an, welchen der Konsument maximal zu zahlen bereit ist und sofern dieser über den Grenzkosten
liegt. Dadurch erhöht sich der Gewinn der Firma und die Konsumentenrente geht gegen null. Die
Produzentenrente entspricht dann der Gesamtrente.
3
Musterlösung 5
Ökonomie
HS 12
In diesem Fall entsteht trotz Monopol kein Wohlfahrtsverlust, da die Angebotsmenge gleich gross ist
wie bei vollkommener Konkurrenz.
P
Produzentenrente = Gesamtrente
Cournot-Punkt
Grenzkosten
Nachfrage
Grenzerlös
x
4