Aufgaben - SeiMedia

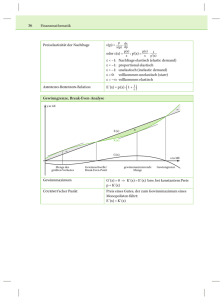
1.2.2 Grafische Darstellung und Analyse der Preisbildung
VOLKSWIRTSCHAFTSLEHRE
© SEI
Klasse: __________
Datum: ___________
Thema: Preisbildung im vollkommenen Angebotsmonopol
Arbeitsauftrag
Bearbeiten Sie die folgenden Aufgaben!
rechnen
zeichnen
schreiben
Partnerarbeit
30 Minuten / HA
Aufgaben
Aufgabe 1
Die Preis-Absatz-Funktion eines Monopolisten hat folgende Gestalt:
10.000 - 2 p
® p = 5.000 - 500 · x
1.000
E = (5.000 - 500 · x) · x
x=
E = 5.000 · x - 500 · x²
E' = 5.000 - 1.000 · x
Dabei bedeuten x = Menge und p = Preis.
Die fixen Kosten (Kf) betragen 2.000 GE, die variablen Kosten (Kv) 2.000 GE je Mengeneinheit (GE = Geldeinheit).
Kv = 2.000 · x è K = 2.000 + 2.000 · x
K‘ = 2.000
x
10
9
8
7
6
5
4
3
2
1
p
E=x·p
E‘
K = Kf + Kv
K‘
G=E–K
a) Füllen Sie die obige Wertetabelle aus!
1
b) Stellen Sie die Kurven in zwei Abbildungen dar und ermitteln Sie dabei grafisch die relevanten Punkte und Zonen: Erlösmaximum, Gewinnmaximum, Gewinnschwelle, Gewinngrenze, Gewinnzone, Verlustzonen, Preis-Absatz-Funktion, Cournot’scher Punkt, Bedingung für das Gewinnmaximum im Monopol (E‘ = K‘).
1.2.2 Grafische Darstellung und Analyse der Preisbildung
Aufgabe 2
Ein Monopolist sieht sich folgender Nachfragesituation gegenüber:
Absetzbare
Menge x
0
1
2
3
4
5
6
7
8
Preis p
4.000
3.500
3.000
2.500
2.000
1.500
1.000
500
0
Erlös E
Gesamtkosten K
Grenzkosten K‘
Gewinn G
Seine fixen Kosten betragen 2.000 GE, seine variablen Kosten 1.000 GE je Produktionseinheit.
Füllen Sie zunächst die Tabelle aus!
Bestimmen Sie grafisch das Gewinnmaximum mithilfe
a) der Gesamtdarstellung (mit Gesamtkosten, Fixkosten und Umsatzerlösen) und
b) der Stückdarstellung (Grenzerlös und Grenzkosten).
Die Preis-Absatz-Funktion, die sich aus der oberen Tabelle ergibt ist in die Stückdarstellung
zu integrieren.
Hinweis:
In dieser Aufgabe liegt keine mathematische Gleichung für die Preis-Absatz-Funktion vor; sie
lässt sich nur aufgrund der Tabelle zeichnen. Daher ist es auch nicht möglich, die Grenzerlöse zu berechnen. Dennoch lässt sich die Grenzerlöskurve zeichnen. Solange die Erlöskurve
eine Parabel darstellt, ist die Grenzerlöskurve eine Gerade mit fallender Steigung. Der yAchsenabschnitt liegt an der gleichen Stelle wie der y-Achsenabschnitt der Preis-AbsatzKurve (hier 4.000), der x-Achsenabschnitt in der Mitte zwischen dem Ursprung und dem xAchsenabschnitt der Preis-Absatz-Kurve, also bei 4 (da der x-Achsenabschnitt der PreisAbsatz-Kurve bei 8 liegt).
2