Beschleunigung bei gleichförmiger Kreisbewegung
Werbung
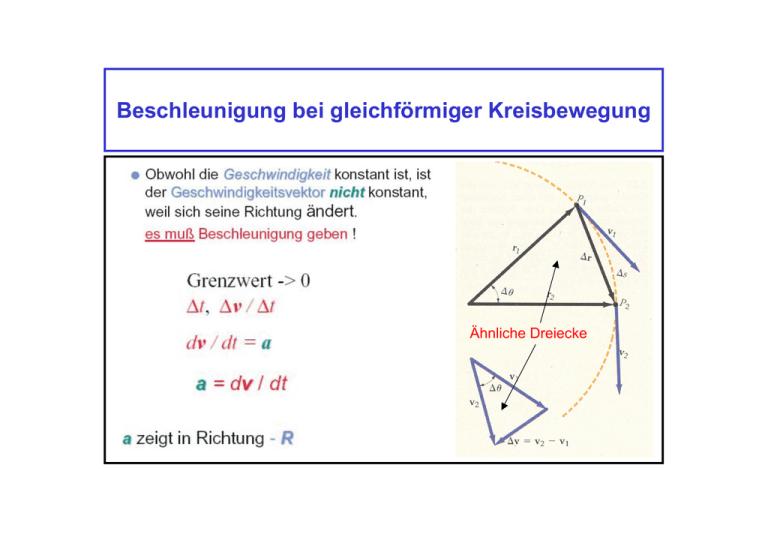
Beschleunigung bei gleichförmiger Kreisbewegung Ähnliche Dreiecke Beschleunigung bei gleichförmiger Kreisbewegung v = ω ⋅R ⇒ a = ω2 ⋅ R Die drei Newtonschen Axiome Isaac Newton, * 25.12.1661 Woolsthorpe, + 20.3.1727 London Principia Mathematica (1687) Die drei Newtonschen Axiome Erstes Newtonsches Axiom (Trägheitsgesetz) Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Bewegung, solange keine äußere Kraft auf ihn wirkt Die drei Newtonschen Axiome Zweites Newtonsches Axiom (Grundgesetz der Dynamik) Es existiert eine von Masse und Geschwindigkeit abhängende Größe, der sogenannte Impuls. Er ist definiert als G G p = m ⋅v Die zeitliche Änderung des Impulses eines Systems ist gleich der Kraft . G G F = dp /d t Meist ist m = const (nicht bei Raketen und in der relativistischen Mechanik). Es gilt dann G G F = m ⋅ a, Kraft = Masse mal Beschleunigung Die drei Newtonschen Axiome (Kraft) Einheit der Kraft ist das Newton (N): Die Kraft, die benötigt wird, der Masse 1 kg die Beschleunigung 1 m/s² zu erteilen. 1 N = 1 kg ⋅ 1 m/s² = 1 m ⋅ kg/s². Nützlich:1 kg = 1N⋅s2/m Kräfte: Gravitation Kräfte: Gravitation ausgeübt wird, ist G = Gravitationskonstante Kräfte: Gravitation Gewicht 6 3 R m ( 6.378 ⋅ 10 ⋅ m) −11 m = 6.673 ⋅ 10 = 9.81 ⋅ 2 ⋅ G = g⋅ kg ⋅ s2 s 5.974 ⋅ 10 24 ⋅ kg ME 2 E 2 Aufgabe: Kraft und Beschleunigung M⋅m M M Lösung: F = G ⋅ 2 ∝ 2 ⇒ X ME R R RX2 2 300/20 = = 0,75 2 RE 2. Newtonsches Axiom: Träge und schwere Masse Träge Masse Schwere Masse widersetzt sich der Beschleunigung verantwortlich für Gravitation F = mt ⋅ a Ms ⋅ ms F = G⋅ R2 Versuch: Träge und schwere Masse Pendel: d 2s d 2 (l ⋅ ϕ) −ms ⋅ g ⋅ sin ϕ ≈ −ms ⋅ g ⋅ ϕ = mt ⋅ 2 = mt ⋅ dt dt 2 ⎛ ms ⋅ g ⎞ Lösung für ϕ(0) = ϕ0 ,ϕ(0) = 0 : ϕ = ϕ0 ⋅ cos ⎜⎜ ⋅ t ⎟⎟ m ⋅ l t ⎝ ⎠ ω= 2π ms ⋅ g mt ⋅ l ⇒T = = 2π ⋅ ω mt ⋅ l ms ⋅ g Periodendauer für mS = mT l T = 2π ⋅ g Stimmt die Annahme ms = mt?? Versuch: Äquivalenz von schwerer und träger Masse Zwei Fadenpendel gleicher Länge (l ≈ 1 m). • Sehr unterschiedliche Massen: gleich große Kugeln aus Plastik bzw. Gusseisen! • Abstand ca. 60 cm. • Gegenphasige Schwingungen • Phase bleibt über mehr als 10 volle Schwingungen erhalten. • mt/ms unabhängig von der Art des Körpers!! 3. Newtonsches Axiom Drittes Newtonsches Axiom (Reaktionsgesetz, actio = reactio) Übt Körper 1 auf Körper 2 eine Kraft aus, so reagiert Körper 2 mit einer im Betrag gleichen, entgegengesetzt gerichteten Kraft G G F ′ = −F Versuch: Kraft erzeugt Gegenkraft (3. Newtonsches Axiom) Versuchsgerät: Zwei mit Rädern versehene Bretter und langes Seil. Start: Wägen in etwa 10 m Entfernung voneinander. Zwei Versuchspersonen annähernd gleicher Masse auf den Wägen mit den Enden des Seils in der Hand. Versuchsablauf: Eine Person hält das Seil fest, die andere zieht. Beobachtung: Beide Wagen setzen sich in Bewegung und treffen sich in der Mitte. Wiederholung mit vertauschten Rollen. Beispiel Beispiel Drei wirksame Kräfte: i) Gewichtskraft FG, ii) Normalkraft FN, iii) Schiebekraft Fx. y FX = m ⋅ aX ⇒ aX = FX / m = 5m/s2 N − m ⋅ g = m ⋅ aY Fx x aY = 0 ⇒ N = m ⋅ g FG=m·g FN=N Aufgabe: Schiefe Ebene Schiefe Ebene Winkel einer schiefen Ebene Schiefe Ebene..... θ Dynamik mit mehreren Körpern Atwoodsche Fallmaschine Atwoodsche Fallmaschine Atwoodsche Fallmaschine - Atwoodsche Fallmaschine Macht das Ergebnis Sinn ? (Grenzfälle prüfen !) Bezugssysteme und Scheinkräfte Man kann zur Beschreibung von mechanischen Vorgängen verschiedene Bezugssysteme verwenden. Beispiel: Bezugssystem S‘ y y‘ Bezugssystem: S G v Geschwindigkeit des Fahrzeugs x‘ x „Ruhendes Bezugssystem“: S (x,y,z) „Bewegtes Bezugssystem“: S‘ (x‘,y‘,z‘) Inertialsysteme Sind zur Beschreibung der Mechanik alle Bezugssysteme gleich gut geeignet? Nur Inertialsysteme sind geeignet! Weil nur in ihnen die Newtonsche Bewegungsgleichung: G G F = m⋅a gilt. Was ist ein Inertialsystem? 1) Ein relativ zu einem Inertialsystem gleichförmig-geradlinig bewegtes System ist ebenfalls ein Inertialsystem. 2) Ein relativ zu einem Inertialsystem beschleunigtes System ist kein Inertialsystem Beispiel: • Strasse Inertialsystem ⇒ Auto mit konstanter Geschwindigkeit auch Inertialsystem. • Beschleunigendes Auto kein Inertialsystem. • Relativ zu Inertialsystem rotierendes System kein Inertialsystem. Inertialsystem (Forts.) Die Erde ist deshalb, streng genommen, kein Inertialsystem a) wegen ihrer Eigenrotation, b) wegen ihrer Beschleunigung bei der Bewegung um die Sonne. Für viele Zwecke kann man ein erdbezogenes Bezugssystem aber mit hinreichender Genauigkeit als Inertialsystem betrachten. Will man in einem Bezugssystem, das kein Inertialsystem ist, die Newtonsche Bewegungsgleichung benutzen, dann muss man sogenannte Scheinkräfte einführen Beispiel: Freier Fall im Aufzug Festhängend G G Ft = −m ⋅ g Freier Fall G a=0 G G FS = m ⋅ g G G FS = m ⋅ g • Experimentator auf festem Boden (Inertialsystem): Aufzugskabine fällt beschleunigt wie Masse m ⇒ keine Relativbewegung. • Experimentator im Aufzug: Auf die Masse m wirkt außer der Schwerkraft eine diese kompensierende Scheinkraft: Schwerelosigkeit Versuch: Gewichtskraft beim freien Fall Auf ein Aluminiumgerüst, wie abgebildet, werden drei Holzklötze mittig platziert. Der mittlere Klotz ist dabei mit einer Gummischnur versehen, die so fest gespannt wird, dass der Klotz gerade noch in seiner Position gehalten wird. Nun lässt man die gesamte Apparatur einige cm nach unten fallen. Beobachtung: Sobald alles nach unten fällt, wird das mittlere Klötzchen in Richtung Gummischnur herausgezogen. Allgemein In einem beschleunigten System kann man die Newtonsche Bewegungsgleichung „retten“, indem man eine auf eine Masse wirkende Trägheitskraft G G Ft = − m ⋅ a einführt. Rotierende Bezugssysteme Zentripetalbeschleunigung / Zentrifugalbeschleunigung Inertialsystem: Körper auf Kreisbahn; Zentripetalbeschleunigung durch Zugkraft im Seil. G Fp = − m ⋅ ω ⋅ r , 2 Auf der Scheibe: Körper in Ruhe (a=0); Zentripetalkraft und Zentrifugalkraft (Scheinkraft) ergänzen sich zu Null. G G Fz = m ⋅ ω 2 ⋅ r G G Fp + Fz = 0 Corioliskraft d Ball fliegt eine Strecke d mit Geschwindigkeit v = d t . Währenddessen bewegt sich der Fänger um s = d ⋅ ω ⋅ t. Beobachter auf Scheibe schreibt das Züruckbleiben des Balls einer Beschleunigung a zu: − s = −d ⋅ ω ⋅ t = 1 2 ⋅ a ⋅ t2 ! So ergibt sich a = −2 ⋅ ω ⋅ d /t, also FC = m ⋅ a = −2 ⋅ m ⋅ ω ⋅ v . Corioliskraft - Versuch Gustave Gaspard de Coriolis (1792- 1843) französischer Mathematiker • Luftpistole auf Drehteller. • Mündung genau im Drehzentrum. • Zielscheibe mit Kugelfang, fest mit Drehteller verbunden. • Zielscheibe justiert: Schuss aus Pistole trifft genau das Zentrum, wenn Anordnung in Ruhe • Aufbau in Drehbewegung (bis max. etwa 1U/sec.). • Einschuss um einige Zentimeter aus dem Zentrum versetzt. s = d·ω·t = d²·ω/v ≈ ≈ 4.0 m²·0.5s-1/(100 m/s) ≈ 2 cm. Corioliskraft Die Corioliskraft steht senkrecht auf der Drehachse des Bezugssystems und der Bewegungsrichtung. Ihr Betrag ist: Fc = −2 ⋅ m ⋅ v ⋅ ω ⋅ sinθ m,v = Masse, Geschwindigkeit des Körpers, w = Kreisfrequenz der Rotation, θ = Winkel zwischen Bewegungsrichtung und Drehachse. Entfernt sich der Körper von der Drehachse, so wirkt die Corioliskraft entgegen der Rotationsrichtung, nähert er sich der Achse, wirkt sie in Rotationsrichtung. G Vektorprodukt von ω und v G G G G Fc = −2 ⋅ m ⋅ (ω × v ) Vektorprodukt (Kreuzprodukt) Drehgeschwindigkeit v kann vektoriell beschrieben werden G G G G v = v0 + ω × r mit vo als Geschwindigkeit des Drehpunktes. Corioliskraft /Hochdruckgebiete G G G Fc = −2 ⋅ m ⋅ (ω × v ) ω v v⊥ v|| v v⊥ ω G −ω × v G v ⊥⊗ G G (ϖ × v ) G Erde Nordhalbkugel: nach rechts Südhalbkugel: nach links ω G v⊥ G G ω×v ⊗ Fc v G G −ω × v ⊥ Fc Coriolisablenkung von Luftströmungen ω aus Tafelebene : Zyklone = Tiefdruckgebiet Antizyklone = Hochdruckgebiet Reibung Reibung Reibung • Die Reibungskraft (Vektor) steht senkrecht auf der Normalkraft N • Für den Betrag der Reibungskraft |fF| gilt |fF| = µK·|N| (= µK|m·g|) Die Konstante µK heißt Gleitreibungszahl Modell..... G µK ⋅ m ⋅ g Reibung und schiefe Ebene Sonderfall:θ = π /2 ⇒ a = g Reibung: Versuch Abhängigkeit der Reibung von der Oberfläche Drei Messingklötze mit unterschiedlicher Beschichtung (ohne, Filz, Antirutschmatte) werden auf eine große Holzplatte gelegt. Hebt man nun die Holzplatte an einer Seite an, so entsteht eine schiefe Ebene. Je nach Art der Beschichtung beginnen die Klötze bei unterschiedlichen Winkelnsich zu bewegen und rutschen dann unterschiedlich schnell. Filz Messing Übergang Haftreibung - Gleitreibung Ein Körper haftet zunächst an der Oberfläche, selbst wenn man eine Kraft F in horizontaler Richtung ausübt. Erst wenn die eingesetzte Kraft die maximale Haftreibungskraft übersteigt, beginnt der Körper zu gleiten. Haftreibung (µS) und Gleitreibung (µK) Haft-R. Gleit-R. µs µk Versuch: Gleitreibung - Haftreibung Kurzbeschreibung: Ein Besenstiel wird auf die beiden ausgestreckten Zeigefinger gelegt. Dann nähert man die Finger einander, bis sie sich berühren, wobei der Stiel abwechselnd auf dem einen und dann auf dem anderen Finger rutscht, bis ihn die Finger genau im Schwerpunkt unterstützen. Warum?? Ein Finger rutscht jeweils so lange bis die wachsende Belastung den Gleitreibungswiderstand größer werden lässt als die Haftreibung am anderen Finger. Haftreibung..... µS = tanθ = 1: θ = 45º Experiment: Haftreibung am Steilhang (Keil) Zwei Holzkeile, deren Steilflächen mit Antirutschmatten beklebt sind, werden mit diesen Flächen aufeinandergestellt. Bei 60º Neigung kann man sie noch mit 2 kg belasten! Reifen und Bremsen ABS = Anti-Blockier-System • Haftreibung > Gleitreibung • ABS: Blockieren verhindert • Bei Blockiergefahr eines Rades wird auch Bremsdruck am anderen Rad moduliert Winterreifen • Weichere Gummimischung: µ größer, • Gröberes Profil: mehr Haftung bei Schnee; Eis??











