1 Beispiel 4 (Einige weitere Aufgaben) Aufgabe 1 Bestimmen Sie für

1
Beispiel 4 (Einige weitere Aufgaben)
Aufgabe 1
Bestimmen Sie für die folgenden Zweierstichproben, d. h. Stichproben, die jeweils aus zwei
Beobachtungen bestehen,
a)
den Durchschnitt x
b)
die mittlere quadratische Abweichung (Varianzen) s2
c)
die Streuung s
s
d) den Variationskoeffizienten v=
x
für jeden der unten angegebenen sieben Fälle und diskutieren Sie, wie die vier Größen
zusammenhängen. Beantworten Sie insbesondere, ob und welche "Gesetzmäßigkeiten" Sie
erkennen!
Beobachtungen
Fall 1
1
2
Fall 2
2
-2
Fall 3
-1
3
Fall 4
1
5
Fall 5
-5
-1
Fall 6
4
-4
Fall 7
8
-8
Lösung:
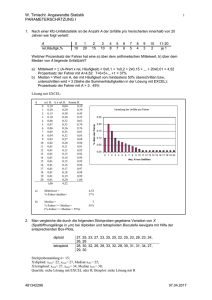
Das Streudiagramm der Zahlen (x 1. Spalte, y = 2. Spalte)
2
Aufgabe 2
Man errechne für die Datenreihe
10, 15, 13, 18, 25, 31, 26, 24, 20, 18, 15, 12, 15, 20, 18
a) die Spannweite
b) den Quartilsabstand
c) die mittlere absolute Abweichung vom Median.
Lösung:
a)
Spannweite: 31- 10 = 21
b)
Die Reihe sortiert ergibt: 10, 12, 13, 15, 15, 15, 18, 18, 18, 20, 20, 24, 25, 26, 31; n=15,
Median 8. Beobachtung: 18
Quartil 1-- 4. Beobachtung: 13; Quartil 3 -- 12. Beobachtung: 24
c) [18-10 + 18-12 + 18-13 + 3(18-15) + 2(20-18) + 24-18 + 25-18 + 26-18 + 31-18]/15
= [8 + 6 + 5 + 9 + 4 + 6 + 7 + 8 + 13]/15 = 66/15 = 4.4
3
Aufgabe 3
Diskutieren Sie den Vorschlag des sog. optimalen Wertpapierportefeuilles, der sagt,
Wertpapiere eines Portefeuilles sollten zumindest zwei Forderungen genügen:
(a) Der Mittelwert µ (Durchschnitt) der Rendite sollte bei gleicher Varianz σ2
(Streuung σ) der größte sein.
(b) Bei gleicher Durchschnittsrendite µ sollte die Streuung σ möglichst klein sein.
Stellen Sie diesen Vorschlag graphisch dar!
Hinweis 1:Nehmen Sie dabei an, die in Frage kommenden Wertpapiere haben alle eine
positive Rendite.
Hinweis 2:Illustrieren Sie Ihre Graphik mit sechs Wertpapieren für die Sie die
Durchschnittsrendite und Streuung aus den vergangenen zwölf
Monatsbeobachtungen haben:
(µ1, σ1), (µ2, σ2), …., (µ6, σ6).
Ein mögliches Beispiel von sechs Wertpapieren ist das folgende:
µi
σi
Wertpapier 1
1.5
1.2
Wertpapier 2
2.5
1.7
Wertpapier 3
8.7
12
Wertpapier 4
4.3
4.5
Wertpapier 5
2.3
1.2
Wertpapier 6
4.3
7.9
Lösungshinweis
Benutzen Sie das Streudiagramm der Zahlen (x = 1. Spalte, y = 2. Spalte)
4
Aufgabe 4
Bestimmen Sie für die folgenden 12 Beobachtungen, abgeschlossene Dienstjahre der 12
Bediensteten des Postamts Hamburg 45:
{ 3, 5, 2, 7, 3, 4, 1, 6, 3, 4, 7, 3 }
a) die Spannweite
b) den Mittelwert
c) die Varianz und Streuung
d) den Median sowie die vier Quartile
Lösung
a) [1, 7], d.h. 6
b) (3+5+2+7+3+4+1+6+3+4+7+ 3)/12 = 48/12 = 4
c) [(3-4)2 + (5-4)2 + (2-4)2 + (7-4)2 + (3-4)2 + (4-4)2 +
(1-4)2 + (6-4)2 + (3-4)2 + (4-4)2 + (7-4)2 + (3-4)2 ]/12 =
1
[12 + 12 + 22 + 32 + 12 + 02 + 32 + 22 + 12 + 02 + 32 + 12 ]/12 = 40/12 = 10/3 = 3
3
10
10
=
= 3.3 = 1.8257,
3
3
bzw. s ≈ 1.8, da nach den großen Einmaleins 18x18 = 324
d) Für Median und Quartile sind die Beobachtungen zu ordnen:
{ 3, 5, 2, 7, 3, 4, 1, 6, 3, 4, 7, 3 } ⇔ { 1, 2, 3, 3, 3, 3, 4, 4, 5, 6, 7, 7}
∴ Der Median ist 3 (die sechste Beobachtung von insgesamt 12); die Quartile folgen
ebenso Q 1 = 3, Q2 = 3, Q3 = 5, Q4 = 7. ⇔ { 1, 2, 3, 3, 3, 3, 4, 4, 5, 6, 7, 7}
s=
Aufgabe 5
Die folgenden n Beobachtungen seien die Zahl der Kinder von jeweils n Familien (nach W.
Krämer, Statistik verstehen, Campus, 1992):
{ 0, 0, 0, 0, 1, 2, 3, 3, 6 }
n= 9
{ 0, 0, 0, 0, 1, 2, 2, 3, 3, 6 } n = 10
{ 0, 0, 0, 0, 1, 2, 3, 3, 9 }
n= 9
{ 0, 0, 0, 0, 1, 2, 3, 3, 18 }
n= 9
a) Bestimmen Sie jeweils den Median.
b) Wie empfindlich ist der Median im Vergleich zum Mittelwert?
Lösung
a) Für den Median sind die Beobachtungen zu ordnen, was hier bereits erfolgt ist.
∴ Im Fall 1: Der Median ist 1 (die mittlere Beobachtung von insgesamt 9);
im Fall 2: der Median ist ebenfalls 1, die letzte Beobachtung der ersten Hälfte,
die 5. von 10 Beobachtungen,
im Fall 3: der Median ist ebenfalls 1.
im Fall 4: der Median ist ebenfalls 1.
b) Für den Vergleich zum Mittelwert gilt es, Fall 1, 3 und 4 zu vergleichen:
M
D
1
15/9 = 5/3
1
18/9 = 6/3 = 2
1
27/9 =9/3 = 3
M.a.W. der Median ist sehr insensitiv auf Datenänderungen, nicht jedoch so der Mittelwert
(Ausreißerproblem)
5
Aufgabe 6
Eine Verwaltung wird auf ihre Effizienz hin überprüft, indem untersucht wird welche
Wartezeit zwischen einem eingehenden Antrag und dessen Bearbeitungsbeginn verstreicht. Dabei ergab sich folgende Häufigkeitstabelle:
Anzahl der verstreichenden Tage
Anzahl der Anträge
0 1 2 3 4 5 6 7 8 9 10
______________________________
1 2 5 6 6 20 25 15 5 5 10
a) Zeichnen Sie das Stabdiagramm und die empirische Verteilungsfunktion F.
b) Welcher Anteil der Anträge muß
- mindestens 6 Tage
- mehr als 6 Tage
- höchstens 3 Tage
auf seine Bearbeitung warten?
d) Geben Sie den Modus und den Median an.
e) Bestimmen Sie den Mittelwert, die mittlere quadratische Abweichung, die
Standardabweichung und den Variationskoeffizienten.
Aufgabe 7
An einem Baggersee B wird täglich die Wassertemperatur X (in Grad Celsius) gemessen.
Man erhält folgende klassifizierte Meßergebnisse:
Temperatur
Anzahl Messungen
____________________________
14 ≤ x < 16
16 ≤ x < 18
18 ≤ x < 20
20 ≤ x < 22
22 ≤ x ≤ 24
15
10
18
12
5
a) Ermitteln Sie die empirische Dichte f und die empirische Verteilungsfunktion F der
Wassertemperatur an den Klassenobergrenzen.
b) Zeichnen Sie das Histogramm sowie den Graphen der Verteilungsfunktion.
c) Berechnen Sie den Median, die durchschnittliche Temperatur und die empirische
Standardabweichung der Temperatur im See.
d) Für welche Temperatur a gilt: F(a) = 0.40 ?
e) Wie groß ist der Anteil der Messungen, bei denen die Wassertemperatur von 20.5 Grad
nicht überschritten worden ist?
6
Aufgabe 8
Man betrachtet die Anzahl X der Zigaretten, die pro Person innerhalb einer Stunde in
einem Raum mit 50 Personen geraucht wurden. Man erhielt folgendes Ergebnis:
Anzahl der Zigaretten
0
1
2
3
Anzahl der Personen
10
5
10
25
a) Berechnen Sie die durchschnittliche Anzahl X von Zigaretten pro Person im
Raum.
b) Berechnen Sie die empirische Standardabweichung der Anzahl von
Zigaretten pro Person im Raum.
c) Berechnen Sie den Wert der empirischen Verteilungsfunktion an der Stelle 2.2.
Aufgabe 9
Eine Größe X nimmt die drei Werte 1, 2 und 3 mit jeweils gleicher Häufigkeit p an.
Bestimmen Sie allgemein:
a)
das arithmetische Mittel,
b) die mittlere quadratische Abweichung,
c)
die Streuung der Größe und ihre Spannweite
Aufgabe 10
Bestimmen Sie für die drei Häufigkeitsverteilungen
a)
h[X=100]
h[X=1]
h[X=0]
= 0.0001
= 0.9900
= 0.0099
b)
h[X= -1]
h[X= +4]
= 1/36
= 35/36
c)
h[X= - 1.5] = 11/36
h[X= +16.0] = 25/36
das arithmetische Mittel und die mittlere quadratische Abweichung (empirische Varianz)
Lösung:
a) E(X) = 1, var(X) = 0.99
b) E(X) = 139/36 ≈ 3.86 , var(X) = 0.99
c) E(X) = 767/72 ≈ 10.65 , var(X) = 0.99
7
Aufgabe 11 (Eine Frage zum Unterschied von Median und Mittelwert)
Vergleichen Sie die drei folgenden Häufigkeiten
Verteilung 1
Wert
Häufigkeit
Verteilung 2
Wert
Häufigkeit
Verteilung 3
Wert
Häufigkeit
1
2
3
4
10
0.2
0.2
0.2
0.2
0.2
1
2
3
4
10
0.3
0.2
0.2
0.2
0.1
1
2
3
4
5
0.2
0.2
0.2
0.2
0.2
a) Für welche Verteilung liegt der Median über dem Mittelwert, für welche darunter,
für welche sind beide Werte gleich?
b) Welche der drei Verteilungen wäre die Verteilung, die sich am besten als eine
Verteilung der Vermögen in der Bundesrepublik eignet
Lösung
zu a) M = 2.5 = 3, D = 4; M = 2, D = 3.1; M= 2.5 = 3, D = 3
zu b) D soweit weit möglich über M, also Verteilung 1 oder 2, nicht ganz einfach zu
entscheiden
Aufgabe 12
Nach einem Marathonlauf werden 50 zufällig ausgewählte Läufer auf ihren Gewichtsverlust Y hin untersucht. Es ergeben sich folgende Werte:
Klasse
Gewichtsverlust (in kg)
Anzahl der Läufer
1
[0,3)
16
2
[3,4)
12
3
[4,6]
22
a) Bestimmen Sie die empirische Verteilungsfunktion F(Y) an den Klassenobergrenzen.
b) Wie groß ist der Anteil der Läufer mit einem Gewichtsverlust Y bis zu 3.25 kg ?
c) Wie hoch ist (approximativ) das arithmetische Mittel des Gewichtsverlustes Y?
d) Welche (approximative) Standardabweichung hat der Gewichtsverlust Y?
8
Aufgabe 13
Für Saatkartoffeln wurde die Anzahl Z der "keimfähigen Augen" ermittelt. Für Kiste 1
ergaben sich folgende Werte:
Anzahl der Kartoffeln
Anzahl der "keimfähigen Augen"
10
6
40
5
30
8
20
10
a) Errechnen Sie das arithmetische Mittel sowie die empirische Streuung des
Merkmals Z für Kiste 1.
b) Für Kartoffeln in den Kisten 2 und 3 ergaben sich folgende Werte:
Kiste 2
Kiste 3
Anzahl der Kartoffeln
40
60
Arithmetisches Mittel des Merkmals Z
7
6
Empirische Streuung des Merkmals Z
5.8
4.4
Berechnen Sie das arithmetische Mittel sowie die Standardabweichung des Merkmals Z
für Kartoffeln aus allen drei Kisten.