Klassisch : Ort und Impuls sind gleichzeitig und unabhängig von

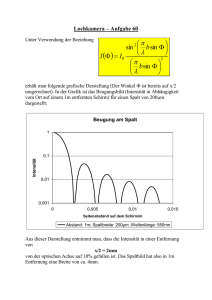
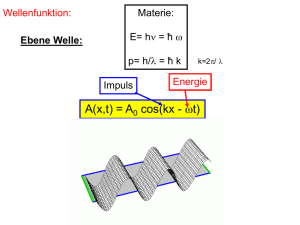
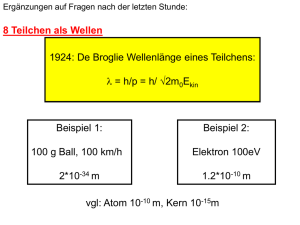
1.3.2 Unschärferelation
Klassisch :
Ort und Impuls sind gleichzeitig und unabhängig
von einander messbar
1.3.2 Unschärferelation
Ort eines Teilchens kann nicht
beliebig genau festgelegt
werden, ohne seinen Impuls zu
beeinflussen.
1.3.2 Unschärferelation
Klassisch :
Ort und Impuls sind gleichzeitig und
unabhängig von einander messbar
QM :
Ortsmessung (durch Huhn) beeinflusst
Impuls (Fuchs)
Versuch 1 : (Analogiebetrachtung) : Beugung bei Wasserwellen
• Ebene Wellenfront bewegt sich exakt in z-Richtung, die x-Komponente der
Geschwindigkeit ist null
y
x
z
Versuch 1: (Analogiebetrachtung) : Beugung bei Wasserwellen
• Durch einen Spalt der Breite 2Δx soll ein schmaler Streifen der Wellenfront
mit einer möglichst scharf definierten x-Koordinate ausgeblendet werden.
Versuch 1 :(Analogiebetrachtung) : Beugung bei Wasserwellen
• Durch einen Spalt der Breite 2Δx soll ein schmaler Streifen der Wellenfront
mit einer möglichst scharf definierten x-Koordinate ausgeblendet werden.
Durch den Spalt wird die xKoordinate der Wellenfront bis auf
eine Unbestimmtheit Δx festgelegt.
Hinter dem Spalt weisen die
Wellenfronten dann jedoch eine
Geschwindigkeitskomponente in xRichtung auf – und zwar um so
stärker, je schmaler der Spalt ist.
Hinter einem sehr schmalen Spalt
von der Größenordnung der
Wellenlänge ist die
Ausbreitungsrichtung völlig
unbestimmt.
y
x
Spalt
z
c
b=2Δx
c
Ergebnis : Je genauer die Wellenfront auf eine x-Koordinate eingeschränkt wird,
desto stärker weicht die Ausbreitungsrichtung hinter dem Spalt von der
ursprünglich exakt präparierten Ausbreitung in z-Richtung ab.
1.3.2 Unschärferelation
Versuch 1 : Beugung von Wasserwellen am Einfachspalt
Idee : Durch einen Spalt der Breite b=2Δx wird ein schmaler Streifen einer
Wellenfront mit einer möglichst scharf definierten x-Koordinate ausgeblendet
Ergebnis : Je genauer die Wellenfront auf eine x-Koordinate eingeschränkt
wird, desto stärker weicht die Ausbreitungsrichtung hinter dem Spalt von der
ursprünglich exakt präparierten Ausbreitung in z-Richtung ab.
Versuch 2 : Beugung eines Laserstrahls am Einfachspalt
• Photonen eines Laserstrahls werden mithilfe von Linsen so präpariert, dass
sie sich alle sehr genau in z-Richtung bewegen. Der Impuls px in x-Richtung
ist damit nahezu gleich null.
• Mithilfe eines verstellbaren Spaltes soll nun die x-Koordinate der Photonen
bis auf eine Unschärfe Δx genau festgelegt werden, viel genauer, als dies
etwa durch den Durchmesser des Laserstrahls gegeben ist.
• Ergebnis : Analog zu den Wasserwellen wird das Licht am Spalt gebeugt. Die
Photonen erhalten also durch die Präparation der x-Koordinate einen Impuls
Δpx in (positiver oder negativer) x-Richtung. Die sorgsame Präparation des
Impulses px =0 wurde durch die Präparation des Ortes x=0 zerstört : Hinter
dem Spalt ist der Impuls px der Photonen unbestimmt.
Treffen Quantenobjekte auf einen schmalen Spalt, so tritt Beugung auf.
Der Versuch, die x-Komponente des Ortes genau festzulegen, führt zu einer
Unschärfe der x-Komponente des Impulses.
 Folgerung : Es ist nicht möglich, den Impuls und den Ort eines Photons
gleichzeitig mit beliebiger Genauigkeit festzulegen. Diese Aussage gilt auch
für beliebige andere Quantenobjekte.
1.3.2 Unschärferelation
Heisenberg‘sche Unschärferelation
Ort und Impuls eines Quantenobjekts können nicht gleichzeitig beliebig genau
festgelegt werden. Das Produkt aus Ortsunschärfe Δx und Impulsunschärfe Δpx
ℎ
kann nicht kleiner werden als 4𝜋 :
Es gilt die Beziehung Δ𝑥 ∙ ∆𝑝𝑥 ≥
ℎ
4𝜋
Bemerkung: Die Unschärferelation gilt prinzipiell für alle Teilchen, nicht
nur für Quantenobjekte, hat dann aber wegen der im Vergleich zur
Objektgröße sehr geringen Größenordnung keinen nennenswerten
Einfluss.
Unschärfe von Wellenpaketen
Die Ausbreitung von Licht und anderer elektromagnetischer Strahlung lässt
sich mit dem Wellenmodell beschreiben. Wenn dabei von der Wellenlänge λ
und der Frequenz f gesprochen wird, bezieht sich dies auf einen unendlich
lang ausgedehnten Wellenzug. Solch ein Wellenzug wird durch eine zeitlich
unbegrenzte ungedämpfte Schwingung erzeugt, z.B. wenn eine
elektromagnetische Welle durch einen ungedämpft schwingenden
Sendedipol abgestrahlt wird.
Ein einzelnes Teilchen, z.B. ein Photon, kann jedoch vernünftig nur durch ein
räumlich begrenztes Wellenpaket beschrieben werden, das durch ein
entsprechendes zeitlich begrenztes Schwingungspaket erzeugt wurde. Ein
solches Schwingungspaket wird durch Überlagerung von unendlich vielen
Sinus-und Kosinusfunktionen aus einem Frequenzintervall 𝑓 ± ∆𝑓 erzeugt.
Unschärfe von Wellenpakten
Der Gedanke soll anhand eines einfachen Beispiels erläutert werden. Gezeigt
ist in Abbildung a) eine einfache, unendlich ausgedehnte Sinusschwingung mit
der Frequenz f=50 Hz. Eine Überlagerung von drei nahe beieinander
liegenden Frequenzen aus dem Bereich 𝑓 ± ∆𝑓 mit ∆𝑓 = 5hZ ergibt deutlich
voneinander getrennte Schwingungspakete :
Unschärfe von Wellenpakten
Die Überlagerung von immer mehr Frequenzen aus dem gleichen
Frequenzbereich 𝑓 ± ∆𝑓 führt dazu, dass benachbarte Schwingungspakete
immer weiter von einander getrennt werden (Abbildungen b bis d).
Unschärfe von Wellenpakten
Im Grenzfall der Überlagerung unendlich vieler Frequenzen bleibt nur noch
ein einziges Schwingungspaket übrig. Wie gut zu erkennen ist, verändert sich
dabei die Zeitliche Breite 2∙Δt der Schwingungspakete nicht, solange auch Δf
konstant bleibt.
Nebenstehende Abbildung zeigt, wie sich eine Veränderung des Frequenzintervalls Δf
auf die Halbbreite der Schwingungspakete Δt auswirkt : Eine Halbierung der
Frequenzunschärfe Δf bewirkt eine Verdopplung der zeitlichen Unschärfe Δt, was auf
eine indirekte Proportionalität beider Größen hindeutet. Die
Proportionalitätskonstante lässt sich aus den Diagrammen ablesen : Δt∙ Δf = ½ .
Dieser Zusammenhang gilt nicht nur f=50Hz, sondern für beliebige Grundfrequenzen
und wird als akustische Unschärfe bezeichnet.
Unschärfe von Wellenpakten
Bemerkung: Die Anwendung der akustischen Unschärfe auf elektromagnetische
Schwingungen erlaubt einen Schluss auf die Unschärfe elektromagnetischer
Wellenpakete, d.h. auf die Unschärfe von Photonen : Ein Sender emittiert in der
Zeitspanne 2∙Δt ein Wellenpaket von Frequenzen aus einem Intervall der Breite 2Δf. Mit
dem Frequenzintervall Δf ist durch den Zusammenhang zur Energie E=hf ein
Energieintervall, also eine Energieunschärfe ΔE=h Δf verbunden.
Daraus folgt die
Energie- Zeit- Unschärfe ΔE ∙ Δt = h/2.
Für den Impuls ergibt sich über die Geschwindigkeit v des Wellenpakets ein ähnliche
Zusammenhang. Das Wellenpaket legt den Weg Δx in der Zeit Δt = Δx/v zurück. Für die
ℎ
𝑣𝑝
Frequenz f besteht mit den Formeln 𝑓𝜆 = 𝑣 und 𝜆 = 𝑝 der Zusammenhang 𝑓 = ℎ zum
Impuls p. Durch Einsetzen von Δ𝑓 =
sich die
𝑣Δ𝑝
ℎ
Orts- Impuls – Unschärfe Δx Δp = h/2.
und Δt = Δx/v in die Formeln Δt Δf = ½ ergibt
Unschärfe von Wellenpakten
Unschärfe von Wellenpakten
Energie und Dauer bzw. Impuls und Ort eines einzelnen Wellenpaketes können
nicht gleichzeitig beliebig genau bestimmt sein.
Bemerkung: Der Term auf der rechten Seite der Unschärfebeziehung
ℎ
Δ𝑥 ∙ ∆𝑝𝑥 ≥ 4𝜋 hängt von der genauen Gestalt des Wellenpakets ab.
Heisenberg zeigte mit seiner Relation, dass das Produkt aus Orts- und
ℎ
Impulsunschärfe nicht kleiner werden kann als 4𝜋
Übung 7 : Berechnen Sie, welche Impulsunschärfe bei einem Einfachspalt der Breit
b=1,0 nm mindestens zu erwarten ist. Wie wirkt sich diese Impulsunschärfe aus?