Folien zur Vorlesung

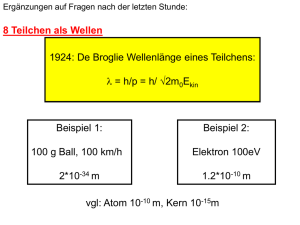
Wellenfunktion:
Ebene Welle:
Materie:
E= h = ħ 
p= h/ = ħ k
Impuls
k=2/ 
Energie
A(x,t) = A0 cos(kx - t)
Wellenfunktion:
Materie:
E= h = ħ 
Ebene Welle:
p= h/ = ħ k
k=2/ 
x px  ħ
Ort x
A(x,t) = A0 cos(kx - t)
x px 
ħ
Extremfall: scharfer Impuls p = ħ k
Völlig delokalisiert (unendlich ausgedehnt)
Impuls px
Wellenfunktion:
Ebene Welle:
A(x,t) = A0 cos(kx - t)
Wellenpaket: Überlagerung aus Ebenen Wellen verschiedenen k
Fourieranalyse: Aufbau aus harmonischen Schwingungen
Visual Quantum Mechanics
Bernd Thaller
Springer, New York 2000
Web Page:
http://www.kfunigraz.ac.at/imawww/vqm/index.html
Aufbau eines Wellenpaketes
Y(x) =  eikx
d.h. die Phasengeschwindigkeit ist Energieabhängig -> Dispersion
Realteil
Real und Imaginaer
Gauss Wellenpaket
Ruhendes Teilchen
Bewegung
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
Ort x
Klassiche Bahn
Quantemechanische Teilchen
x px  ħ
„Wellenpaket“
Ortsunschärfe
x px  ħ
Impuls px
Impuls: Wellenlänge
Unschärfe: verschiedene
Wellenlängen
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
•Wellenlänge länger (langsamer am Scheitelpunkt)
•Ausgedehnter: auseinandergelaufen
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
•Wellenlänge länger (langsamer am Scheitelpunkt)
•Ausgedehnter: auseinandergelaufen
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Doppelspalt:
Höhe: Wahrscheinlichkeit ein Teilchen dort zu finden
ORT: dargestellt
Gausssche Wellenpaket
Gaussverteilung im Ort Impuls
Ort x
Impuls: nicht zu sehen
x px  ħ
Impuls px
Doppelspalt:
ORT: dargestellt
Ort x
Impuls: in der
Wellenlänge
x px  ħ
Amplitude:Farbsättigung
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Impuls px
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Konsequenz:
Potentielle Energie
Klassisch:
Oszillation
zwischen
Potentieller und
kinetischer
Energie
x
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Potentielle Energie
Konsequenz:
Klassisch:
ein Teilchen
kann
in Ruhe am
Boden sitzen
x
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Potentielle Energie
Konsequenz:
QM:
In einem
Potentialtopf
gibts immer eine
„Nullpunktsschwingung“
x
px
x
Heisenbergsche Unschärfe Relation
x px  ħ
ħ = 1 10-34 kg m2/sec
Kugel 10g
auf 1m
Potentielle Energie
10-26 m/sec
x
px
x
Heisenbergsche Unschärfe Relation
x px  ħ
ħ = 1 10-34 kg m2/sec
Elektronen im Atom:
Radius: 10-10m
Elektronenimpuls>10-24 kg m/sec
me=9 10-31kg -> 9 107 m/sec
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Energie/Zeit
t E  ħ
Folgen:
•Monochromatisches Licht kann nicht sehr kurz sein
•Ein kurzlebiger Zustand hat keine scharfe Energie
•Nur stabile Zustände (Bohrmodel) haben scharfe Energie
Energieerhaltung?
kann kurzzeitig verletzt sein!
Gilt streng im Einzelprozess, aber nicht in beliebig kurzen
Zeitintervallen.
Beispiel 1:
t E  ħ
Beispiel 1:
t E  ħ
Klassische Mechanik
Energieerhaltung gilt
für jeden Zwischenschritt
Quantenmechanik
Energieerhaltung gilt für
Zwischenschritte nur innerhalb
t E  ħ
Beispiel 2:
t E  ħ
Kurze Lichtpulse sind breitbandig: t E  ħ = 6.58*10-16 eVs
Ephoton= h 
langer sinus: scharfe Energie
Kurzer Laserpuls
Überlagerung von ebenen Wellen
Bsp: 5*10-15 sec (femto)
0.1 eV (von z.B. 1,5 eV)
•Teilchen durch Wellen beschrieben (de Broglie)
•Die Wellen interferieren
•Amplitudenquadrat ist Wahrscheinlichkeit
•Unschärfe von Ort & Impuls, Energie & Zeit
•Ebene Wellen: Impuls aber kein Ort
•Teilchenanschauung: Wellenpaket
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
Schwarzer Strahler
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
a) Absorbtionsspektren
Wasserstoff
Gas
Wasserstoff
Absorbtionsspektrum
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
a) Absorbtionsspektren
b) Emissionsspektren
Helium
Wasserstoff Emissionsspektrum
Wellenlänge nm
H
Spektralanalyse
Kirchhoff und Bunsen:
Jedes Element hat charakteristische Emissionsbanden
H
1853 von Anders Jonas Angström entdeckt
H
1 Å = 10-10 m
Rydbergkonstante
109678 cm-1
infrarot
sichtbar
ganze Zahlen
ultaviolett
Lyman n1=1
Balmer n1=2
Paschen n1=3
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
10.2. Die Bohrschen Postulate
Wie Rutherford
Elektronen auf Kreisbahnen
Coulomb Anziehung Z=1, e-
Zentrifugalkraft:
mer2
Gesamtenergie des Elektrons auf der Bahn:
E = Ekin + Epot
0
Energy
Epot
r
negativ
Energie die frei wird
wenn Elektron von unendlich
zum Radius r gebracht wird.
Widerspruch zur klassichen
Mechanik & Maxwellgleichungen:
•Bewegte Ladung strahlt Energie ab,
Elektron stürzt in Kern!
•Strahlung ist nicht quantisiert
keine diskreten Linien!
Bohrsche Postulate (Niels Bohr 1913)
•Elektronen bewegen sich auf Kreisbahnen
•Die Bewegung ist strahlungsfrei
rn
n
•Der Drehimpuls der Bahnen ist quantisiert
l=n ħ
(Historisch nicht korrekt)
Ry = Rydbergkonstante (Ionisierungsenergie n=1)
109678 cm-1
Einige Zahlenwerte:
Radius des Wasserstoffatoms
rn=1= 0.529 10-10m
Ionisierungsenergie des
Wasserstoffatoms
En=1= 13.59 eV
Z2 !! dh. Uran 115 keV
Heisenbergsche Unschärfe x px  ħ
10.3 Rydberg Atome
10.3 Rydberg Atome :
n=10 000
Radius = 0.6 mm
En=10 000= 1.3 10-7 eV
0.01 mm wurde wirkliche erreicht!
Rydberg Atome
•rn  n2
•vn  1/n
Heisenbergsche Unschärfe x px  ħ
n!1
Übergang zu klassischer Bahn
(Bohrsches Korrespondezprinzip)
Lebensdauer steigt E3
10.4 Korrektur durch endliche Kernmasse
mproton / melektron = 1836
gemeinsame Bewegung um
Korrektur:
Massenschwerpunkt
Wasserstoff Energie
0.0545 %
10-15m
10-10m
Kerndurchmesser 10-5 des Atoms!
Massenschwerpunkt liegt nicht im Kern
Erinnerung:
Wasserstoff 3 Isotope:
H
1 Proton +
1 Elektron
D (Deuterium)
1 Proton + 1 Neutron + 1 Elektron
T (Tritium)(12.3 y) 1 Proton + 2 Neutronen + 1 Elektron
10.4 Korrektur durch endliche Kernmasse
Folge: Isotope haben verschiedenen Spektrallinien
Korrektur:
Wasserstoff Energie
0.0545 %
mdeuteron / mproton = 2
10.5. Myonische Atome
Elektronenmasse!
 Meson
m = 207 me
10.5. Myonische Atome
Erzeugung von -Mesonen an Protonenbeschleunigern:
p + n -> p + p + -
Pion (Masse 273 me)
2.5 10-8s
- + 
Myon + Myonneutrino
2.2 10-6 s
e- + e + 
Spektrum 207 fach höhere Energie
10.5. Myonische Atome
Wozu?
Myonen Bahnen sind teilweise im Kern
-> Energie gibt Information über Ladungsverteilung des Kerns