Vorlesung-13

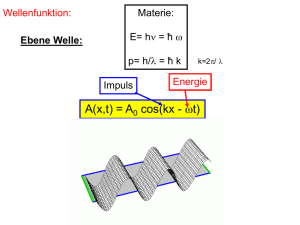
Ergänzungen auf Fragen nach der letzten Stunde:
8 Teilchen als Wellen
1924: De Broglie Wellenlänge eines Teilchens:
 = h/p = h/ 2m0Ekin
Beispiel 1:
Beispiel 2:
100 g Ball, 100 km/h
Elektron 100eV
2*10-34 m
1.2*10-10 m
vgl: Atom 10-10 m, Kern 10-15m
Doppelspalt: Was passiert, wenn man eine Seite zuhält?
Doppelspalt: Was passiert, wenn man eine Seite zuhält?
Schliesse 1 Schlitz NACHDEM das Teilchen emittiert wurde:
Delayed Choice:
Interferenz
z.B. Auslöschung
Delayed Choice:
Schalte Spiegel aus
NACHDEM der Puls durch
den Teiler ist
Keine Interferenz!
Was passiert wenn die Teilchen die Grösse der Schlitze haben?
Auch für Wasserwellen ist die Überlagerung 2er Kugelwellen
eine Idealisierung.
Details hängen von
der Form
der Schlitze ab.
Reibung,
Viskosität,
Wirbel etc
spielen eine Rolle!
Kirchhoff: Beugung am Gitter hängt von der Schlitzbreite ab
He
Teilchenwelle
Gitter
Einhüllende
hängt von Stegbreite
und Schlitzbreite ab.
Kirchhoff: Beugung am Gitter hängt von der Schlitzbreite ab
He
Teilchenwelle
Einhüllende
hängt von Stegbreite
und Schlitzbreite ab.
Toennies & Grisenti
Kirchhoff: Beugung am Gitter hängt von der Schlitzbreite ab
He
Teilchenwelle
Einhüllende
hängt von Stegbreite
und Schlitzbreite ab.
Toennies & Grisenti
Kirchhoff: Beugung am Gitter hängt von der Schlitzbreite ab
He
Teilchenwelle
Gitter
Effektive Schlitzbreite hängt von Teilchendurchmesser ab!
Toennies & Grisenti
9. Heisenbergsche Unschärfe
Heisenbergsche Unschärferelation
x px  ħ
Ort und Impuls eines Teilchens
können nicht genauer bestimmt werden
P= h  / c
Gute Ortsauflösung=
kurze Wellenlänge=
hoher Impuls
Die Messung des Ortes erfordert Streuung von Licht,
Es gibt keine Wechselwirkungfreie Beobachtung
dadurch ist der Impuls nach der Messung geändert
Heisenbergsche Unschärferelation
x px  ħ
Ort und Impuls eines Teilchens
können nicht genauer bestimmt werden
Der Meßprozeß ändert den Zustand
des zu messenden Objektes!
Präzise
Impulsmessung
Objekt in
unbekanntem
Zustand
Präzise Ortsmessung
benötigt grossen
Impulstransfer!
Ort unbekannt,
Impuls bekannt
Objekt wieder in
unbekanntem Impulszustand
Ort bekannt
Heisenbergsche Unschärferelation
x px  ħ
Ort und Impuls eines Teilchens
können nicht genauer bestimmt werden
Der Meßprozeß ändert den Zustand
des zu messenden Objektes!
Die Wechselwirkung kann nicht beliebig klein sein!
(gequantelt!)
Theorie die nicht Aussage über die Welt an sich macht,
sondern nur über mögliche Meßgrössen
QM
Ort x
Px=mdx/dt
Impuls ist NICHT dx/dt
Da wenn x scharf p unscharf
Vorhersage unscharf
Zeit
Zeit
t1
t2
t3
t als Parameter
Impuls px
Ort x
Punkt im
Phasenraum
zu einem
Zeitpunkt
Ort x
Ort x
Klassische Bahn eines Teilchen
x px  ħ
Impuls px
Impuls px
Präzise
Impulsmessung
Objekt in
unbekanntem
Zustand
Ort x
Ort x
x px 
ħ
x px 
ħ
Impuls px
Präzise Ortsmessung
benötigt grossen
Impulstransfer!
Ort unbekannt,
Impuls unbekannt
Objekt wieder
unbekanntem Impulszustand
Ort bekannt
Wellenfunktion:
Licht:
Materie:
E=h
E= h = ħ 
P= h  / c
p= h/ = ħ k
Ebene Welle:
A(x,t) = A0 cos(kx - t)
k=2/ 
Wellenfunktion:
Licht:
Materie:
E=h
E= h = ħ 
P= h  / c
p= h/ = ħ k
k=2/ 
Ebene Welle:
x px  ħ
Ort x
A(x,t) = A0 cos(kx - t)
x px 
ħ
Extremfall: scharfer Impuls p = ħ k
Völlig delokalisiert (unendlich ausgedehnt)
Impuls px
Wellenfunktion:
Ebene Welle:
A(x,t) = A0 cos(kx - t)
Wellenpaket: Überlagerung aus Ebenen Wellen verschiedenen k
Fourieranalyse: Aufbau aus harmonischen Schwingungen
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
Ort x
Klassiche Bahn
Quantemechanische Teilchen
x px  ħ
„Wellenpaket“
Ortsunschärfe
x px  ħ
Impuls px
Impuls: Wellenlänge
Unschärfe: verschiedene
Wellenlängen
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
•Wellenlänge länger (langsamer am Scheitelpunkt)
•Ausgedehnter: auseinandergelaufen
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Beispiel: Schiefer Wurf
 = h/p = h/ 2m0Ekin
•Wellenlänge länger (langsamer am Scheitelpunkt)
•Ausgedehnter: auseinandergelaufen
Siehe movie auf
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
Doppelspalt:
Höhe: Wahrscheinlichkeit ein Teilchen dort zu finden
ORT: dargestellt
Gausssche Wellenpaket
Gaussverteilung im Ort Impuls
Ort x
Impuls: nicht zu sehen
x px  ħ
Movie auf
Impuls px
http://rugth30.phys.rug.nl/quantummechanics/diffint.htm#Double-slit
Doppelspalt:
Movie auf
http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html
ORT: dargestellt
Ort x
Impuls: in der
Wellenlänge
x px  ħ
Amplitude:Farbsättigung
Impuls px
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Konsequenz:
Potentielle Energie
Klassisch:
Oszillation
zwischen
Potentieller und
kinetischer
Energie
x
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Potentielle Energie
Konsequenz:
Klassisch:
ein Teilchen
kann
in Ruhe am
Boden sitzen
x
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Potentielle Energie
Konsequenz:
QM:
In einem
Potentialtopf
gibts immer eine
„Nullpunktsschwingung“
x
px
x
Heisenbergsche Unschärfe Relation
x px  ħ
ħ = 1 10-34 kg m2/sec
Kugel 10g
auf 1m
Potentielle Energie
10-26 m/sec
x
px
x
Heisenbergsche Unschärfe Relation
x px  ħ
ħ = 1 10-34 kg m2/sec
Elektronen im Atom:
Radius: 10-10m
Elektronenimpuls>10-24 kg m/sec
me=9 10-31kg -> 9 107 m/sec
Heisenbergsche Unschärfe Relation
Ort / Impuls
x px  ħ
Energie/Zeit
t E  ħ
Folgen:
•Monochromatisches Licht kann nicht sehr kurz sein
•Ein kurzlebiger Zustand hat keine scharfe Energie
•Nur stabile Zustände (Bohrmodel) haben scharfe Energie
Energieerhaltung?
kann kurzzeitig verletzt sein!
Gilt streng im Einzelprozess, aber nicht in beliebig kurzen
Zeitintervallen.
Beispiel 1:
t E  ħ
Beispiel 1:
t E  ħ
Klassische Mechanik
Energieerhaltung gilt
für jeden Zwischenschritt
Quantenmechanik
Energieerhaltung gilt für
Zwischenschritte nur innerhalb
t E  ħ
Beispiel 2:
t E  ħ
Kurze Lichtpulse sind breitbandig: t E  ħ = 6.58*10-16 eVs
Ephoton= h 
langer sinus: scharfe Energie
Kurzer Laserpuls
Überlagerung von ebenen Wellen
Bsp: 5*10-15 sec (femto)
0.1 eV (von z.B. 1,5 eV)
•Teilchen durch Wellen beschrieben (de Broglie)
•Die Wellen interferieren
•Amplitudenquadrat ist Wahrscheinlichkeit
•Unschärfe von Ort & Impuls, Energie & Zeit
•Ebene Wellen: Impuls aber kein Ort
•Teilchenanschauung: Wellenpaket
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
Schwarzer Strahler
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
a) Absorbtionsspektren
Wasserstoff
Gas
Wasserstoff
Absorbtionsspektrum
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
a) Absorbtionsspektren
b) Emissionsspektren
Helium
Wasserstoff Emissionsspektrum
Wellenlänge nm
H
Spektralanalyse
Kirchhoff und Bunsen:
Jedes Element hat charakteristische Emissionsbanden
H
1853 von Anders Jonas Angström entdeckt
H
1 Å = 10-10 m
Rydbergkonstante
109678 cm-1
infrarot
sichtbar
ganze Zahlen
ultaviolett
Lyman n1=1
Balmer n1=2
Paschen n1=3
9. Heisenbergsche Unschärferelation
10. Das Bohrsche Atommodell
10.1. Diskrete Spektren
10.2. Die Bohrschen Postulate
Wie Rutherford
Elektronen auf Kreisbahnen
Coulomb Anziehung Z=1, e-
Zentrifugalkraft:
mer2
Gesamtenergie des Elektrons auf der Bahn:
E = Ekin + Epot
0
Energy
Epot
r
negativ
Energie die frei wird
wenn Elektron von unendlich
zum Radius r gebracht wird.
Widerspruch zur klassichen
Mechanik & Maxwellgleichungen:
•Bewegte Ladung strahlt Energie ab,
Elektron stürzt in Kern!
•Strahlung ist nicht quantisiert
keine diskreten Linien!
Bohrsche Postulate (Niels Bohr 1913)
•Elektronen bewegen sich auf Kreisbahnen
•Die Bewegung ist strahlungsfrei
rn
n
•Der Drehimpuls der Bahnen ist quantisiert
l=n ħ
(Historisch nicht korrekt)
Ry = Rydbergkonstante (Ionisierungsenergie n=1)
109678 cm-1
Einige Zahlenwerte:
Radius des Wasserstoffatoms
rn=1= 0.59 10-10m
Ionisierungsenergie des
Wasserstoffatoms
En=1= 13.59 eV
Z2 !! dh. Uran 115 keV
Heisenbergsche Unschärfe x px  ħ
10.3 Rydberg Atome
10.3 Rydberg Atome :
n=10 000
Radius = 0.6 mm
En=10 000= 1.3 10-7 eV
0.01 mm wurde wirkliche erreicht!
Rydberg Atome
•rn  n2
•vn  1/n
Heisenbergsche Unschärfe x px  ħ
n!1
Übergang zu klassischer Bahn
(Bohrsches Korrespondezprinzip)
Lebensdauer steigt E3