Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An
Werbung

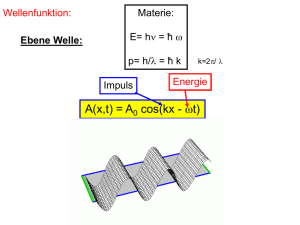
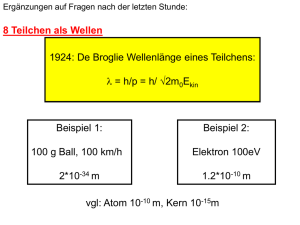
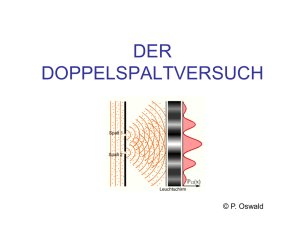
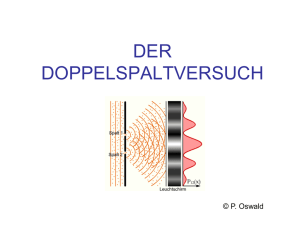
Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An einigen Beispielen erläutern 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Wichtige Punkte: u (ν , T ) = 8πh c 3 e hν 1) Form des Spektrums, Temperaturabhängigkeit ν3 k BT −1 2) Ableitung durch die Annahme das die Oszilatoren in den Wänden quantisierte Energien haben E= nh ν 5. Das Photon: Welle und Teilchen Wellenbild ergibt Blaue Linie: Wahrscheinlichkeitsverteilung der Photonen Einzelne Photonen Verbindung von Wellen und Teilchenbeschreibung: Photonen: Photonendichte = Intensität/ (c h ν) Ebene Welle: Elektrische Feldstärke ∝ cos(ν/2π t) Intensität ∝ E2 Wahrscheinlichkeit für ein Photon zu finden ∝ Quadrat der Amplitude 6. Teilchen als Wellen 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt De Broglie Wellenlänge - Beobachtungen eines Teilchens - Einsteins Interpretation mit Masse m0: - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel λ = h/p = h/ √2m0Ekin 5.5. Licht als Welle und Teilchen 6. Teilchen als Welle (de Broglie) 6.1. Die deBroglie Wellenlänge 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment 6.3 Möllenstedt-Düker Experiment 6.4. Experimente 2: Atome/Moleküle als Welle 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Elektronenquelle Faden+ 0.001 mm! - - Film •Extrem vibrationsarmer Aufbau •Sehr lokalisierte Elektronenquelle 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Zeit 7. Heisenbergsche Unschärferelation Heisenbergsche Unschärferelation Δx Δpx ≥ ħ Ort und Impuls eines Teilchens können nicht genauer bestimmt werden P= h ν / c Gute Ortsauflösung= kurze Wellenlänge= hoher Impuls Die Messung des Ortes erfordert Streuung von Licht, Es gibt keine Wechselwirkungfreie Beobachtung dadurch ist der Impuls nach der Messung geändert 7. Heisenbergsche Unschärferelation Heisenbergsche Unschärferelation Δx Δpx ≥ ħ Ort und Impuls eines Teilchens können nicht genauer bestimmt werden Der Meßprozeß ändert den Zustand des zu messenden Objektes! Die Wechselwirkung kann nicht beliebig klein sein! (gequantelt!) Theorie die nicht Aussage über die Welt an sich macht, sondern nur über mögliche Meßgrössen Ort x Δx Δpx ≥ ħ Objekt in unbekanntem Zustand Δx Δpx ≥ ħ Impuls px Impuls px Präzise Impulsmessung Ort x 7. Heisenbergsche Unschärferelation Präzise Ortsmessung benötigt grossen Impulstransfer! Ort unbekannt, Impuls unbekannt Objekt wieder unbekanntem Impulszustand Ort bekannt 7. Heisenbergsche Unschärferelation Heisenbergsche Unschärferelation Δx Δpx ≥ ħ Ort x Ort und Impuls eines Teilchens können nicht genauer bestimmt werden Δx Δpx ≥ ħ Impuls px Wie passt die Unschärferelation zum Wellenbild? 7. Heisenbergsche Unschärferelation Wellenfunktion: De Broglie Welleneigenschaften der Materie: Materie: Welle: Energie E = hν = ħ ω Frequenz Impuls p = h/λ = ħ k Wellenlänge „Wellenvektor“ k=2π/ λ Impuls Energie „Ebene Welle“ A(x,t) = A0 cos(kx - ωt) 7. Heisenbergsche Unschärferelation Wellenfunktion: Ebene Welle ist ein Extremfall: Ebene Welle beschreibt ein völlig delokalisiertes (unendlich ausgedehntes) Teilchen Impuls Energie „Ebene Welle“ A(x,t) = A0 cos(kx - ωt) Ort x Extremfall: scharfer Impuls p = ħ k Δx Δpx ≥ ħ Impuls px 7. Heisenbergsche Unschärferelation Wellenfunktion: Ebene Welle: A(x,t) = A0 cos(kx - ωt) Wellenpaket: Überlagerung aus Ebenen Wellen verschiedenen k Fourieranalyse: Aufbau aus harmonischen Schwingungen Sehr schöne Webpage: http://www.kfunigraz.ac.at/imawww/vqm/index.html 7. Heisenbergsche Unschärferelation Aufbau eines Wellenpaketes Ψ(x) = ∑ eikx d.h. die Phasengeschwindigkeit ist Energieabhängig -> Dispersion 03_02b.mov Real und Imaginaer 7. Heisenbergsche Unschärferelation Beispiel: Schiefer Wurf λ = h/p = h/ √2m0Ekin Ort x Klassiche Bahn Quantemechanische Teilchen Δx Δpx ≥ ħ „Wellenpaket“ Ortsunschärfe Impulsunschärfe: verschiedene Wellenlängen http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html Δx Δpx ≥ ħ Impuls px 7. Heisenbergsche Unschärferelation Beispiel: Schiefer Wurf λ = h/p = h/ √2m0Ekin •Wellenlänge länger (langsamer am Scheitelpunkt) •Ausgedehnter: auseinandergelaufen http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html 7. Heisenbergsche Unschärferelation Beispiel: Doppelspalt mit Wellenpaket Die stationäre Darstellung des Doppelspaltes mit ebener Welle vor und Kugelwellen nach dem Spalt ist der Extremfall der Unschärferelations mit völlig scharfem Impuls (d.h. fester Wellenlänge) Alternative: Beschreibe Teilchen durch Wellenpaket mit Δx und Δ px anstatt ebener Welle Δy Δx http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html 7. Heisenbergsche Unschärferelation Beispiel: Doppelspalt mit Wellenpaket Höhe: Wahrscheinlichkeit ein Teilchen dort zu finden Alternative: Beschreibe Teilchen durch Wellenpaket mit Δx und Δ px anstatt ebener Welle Δy ORT: Δ x dargestellt Impuls/Wellenlänge: nicht zu sehen Gausssche Wellenpaket Gaussverteilung im Ort Impuls http://www.kfunigraz.ac.at/imawww/vqm/german/wellen3.html 7. Heisenbergsche Unschärferelation Beispiel: Doppelspalt mit Wellenpaket QM-Doppelspalt-mit-phase.mov ORT: dargestellt Impuls: in der Wellenlänge Amplitude:Farbsättigung 7. Heisenbergsche Unschärferelation Die Nullpunktsenergie: Eine Folge der Unschärferelations bei Anwesenheit eines Potentials Δx Δpx ≥ ħ Kugel 10g auf 1μm ħ = 1 10-34 kg m2/sec Potentielle Energie 10-26 m/sec Δx Δpx x 7. Heisenbergsche Unschärferelation Die Nullpunktsenergie: Eine Folge der Unschärferelations bei Anwesenheit eines Potentials Δx Δpx ≥ ħ ħ = 1 10-34 kg m2/sec Elektronen im Atom: Radius: 10-10m Elektronenimpuls>10-24 kg m/sec me=9 10-31kg -> 9 107 m/sec 7. Heisenbergsche Unschärferelation Ort / Impuls Δx Δpx ≥ ħ Energie/Zeit Δt ΔE ≥ ħ Folgen: •Monochromatisches Licht kann nicht sehr kurz sein •Ein kurzlebiger Zustand hat keine scharfe Energie •Nur stabile Zustände (Bohrmodel) haben scharfe Energie Energieerhaltung? kann kurzzeitig verletzt sein! Gilt streng im Einzelprozess, aber nicht in beliebig kurzen Zeitintervallen. 7. Heisenbergsche Unschärferelation Beispiel 1: Δt ΔE ≥ ħ 7. Heisenbergsche Unschärferelation Klassische Mechanik Beispiel 1: Δt ΔE ≥ ħ Quantenmechanik hier weite Energieerhaltung gilt für jeden Zwischenschritt Energieerhaltung gilt für Zwischenschritte nur innerhalb Δt ΔE ≥ ħ 7. Heisenbergsche Unschärferelation Beispiel 2: Δt ΔE ≥ ħ Kurze Lichtpulse sind breitbandig: Δt ΔE ≥ ħ = 6.58*10-16 eVs Ephoton= h ν langer sinus: scharfe Energie Kurzer Laserpuls Überlagerung von ebenen Wellen Bsp: 5*10-15 sec (femto) 0.1 eV (von z.B. 1,5 eV) Wichtige Punkte: •Teilchen durch Wellen beschrieben (de Broglie) •Die Wellen interferieren •Amplitudenquadrat ist Wahrscheinlichkeit •Unschärfe von Ort & Impuls, Energie & Zeit •Ebene Wellen: Impuls aber kein Ort •Teilchenanschauung: Wellenpaket