Geometrie

Geometrie
Homepage zur Veranstaltung: http://www.juergen-roth.de ► Lehre ► Geometrie
Jürgen Roth
Geometrie
5.1
Inhaltsverzeichnis
Geometrie
0 Geometrie!?
1 Axiome der Elementargeometrie
2 Kongruenzabbildungen
3 Längen-, Winkel- und Flächenmessungen
4 Elementare Anwendungen
5 Ähnlichkeitsabbildungen
Jürgen Roth
Geometrie
5.2
Geometrie
Kapitel 5:
Ähnlichkeitsabbildungen
Jürgen Roth
Geometrie
5.3
Inhaltsverzeichnis
Kapitel 5:
Ähnlichkeitsabbildungen
5.1 Zentrische Streckung
5.2 Ähnlichkeitsabbildungen – Ähnlichkeit
Jürgen Roth
Geometrie
5.4
Abbildungsgruppen
Jürgen Roth
Geometrie
5.5
Kapitel 5: Ähnlichkeitsabbildungen
5.1 Zentrische Streckung
Jürgen Roth
Geometrie
5.6
Pantograph
http://www.juergen-roth.de/dynageo/pantograph/
Jürgen Roth
Geometrie
5.7
Dilatation
Definition 5.1
Eine Abbildung der Ebene  auf sich heißt genau dann Dilatation,
wenn sie jede Gerade auf eine zu ihr parallele Gerade abbildet.
Bemerkung: Verschiebungen sind also Dilatationen und nach Satz 2.47
sogar die einzigen, die keinen Fixpunkt besitzen.
Satz 5.1
Bei Dilatationen mit Fixpunkt ist jede Gerade
durch einen Fixpunkt eine Fixgerade.
Beweis: Annahme: Die Gerade g durch einen Fixpunkt Z ist keine Fixgerade.
Dann wird g auf eine von g verschiedene Parallele abgebildet, auf der auch
das Bild von Z liegt. Folglich wäre Z im Wiederspruch zur Voraussetzung kein
Fixpunkt.
Satz 5.2
Eine von der Identität verschiedene Dilatation
hat höchstens einen Fixpunkt.
Jürgen Roth
Geometrie
5.8
Zentrische Streckung
Definition 5.2
Eine Dilatation mit einem Fixpunkt Z heißt zentrische Streckung.
Der Fixpunkt Z heißt Streckungszentrum.
Bemerkung:
Man kann zeigen, dass die
Definition 5.2 gleichwertig zu
folgender Definition 5.3 ist.
Definition 5.3
Eine Abbildung der Ebene  auf sich heißt genau dann
zentrische Streckung ZZ, k mit dem Zentrum Z und dem
Streckungsfaktor k  R\{0}, wenn jedem Punkt P genau
ein Bildpunkt P‘ so zugeordnet wird, das gilt:
Z  PP‘  ZP‘  k  ZP
Jürgen Roth
Geometrie
5.9
Zentrische Streckung
Bemerkungen
Das Bild P‘  ZZ, k(P) von P wird konstruiert, indem man auf der
Geraden ZP von Z aus die |k|-fache Länge der Strecke [ZP]
abträgt, für k  0 auf der Halbgeraden, auf der P liegt, für
k  0 auf der entgegengesetzten Halbgeraden.
Es gibt zwei wichtige Sonderfälle von Definition 5.3:
k  1: Jeder Pfeil wird auf sich selbst abgebildet. Folglich ist die
Identität eine zentrische Streckung mit Streckungsfaktor 1.
k  1: Jeder Pfeil ZP wird auf den Gegenpfeil ZP‘ abgebildet. Also ist
die Punktspiegelung eine spezielle zentrische Streckung mit
Streckungsfaktor 1.
Satz 5.3
Die zentrische Streckung ZZ, k bildet jeden Pfeil AB so auf den Pfeil
A‘B‘ ab, dass gilt:
A‘B‘  k  AB
Jürgen Roth
Geometrie
5.10
Zentrische Streckung
Bemerkung
Eine Strecke wird durch die zentrische Streckung ZZ, k also auf
eine Strecke abgebildet, die die |k|-fache Länge besitzt und deren
Trägergerade für k  0 gleichorientiert, für k  0 entgegengesetzt
orientiert zur Trägergeraden der Originalstrecke ist.
Beweis zu Satz 5.3
ZZ, k ist eine zentrische Streckung mit A‘  ZZ, k(A) und B‘  ZZ, k(B).
1. Fall: Z  AB
(Def. 5.2)
A‘B‘ || AB
ZP  AB  ZP  AB (*)
 PB || ZA
ZP‘A‘B‘  ZP‘  A‘B‘ (**)
 P‘B‘ || ZA‘
ZA  Z‘A‘
(*) (**)
(Def. 5.2)
 PB || P‘B‘  P‘  ZZ, k(P)  ZP‘  k  ZP  A‘B‘  k  AB
Jürgen Roth
Geometrie
5.11
Zentrische Streckung
Beweis zu Satz 5.3 (Fortsetzung)
2. Fall: Z  AB
Zurückführen auf den 1. Fall!
#
Jürgen Roth
Geometrie
5.12
Folgerungen aus Satz 5.3
Satz 5.4: Erster Strahlensatz
Werden zwei von einem Punkt ausgehende
Halbgeraden (oder deren entgegengesetzte
Halbgeraden) von parallelen Geraden geschnitten, dann verhalten sich die Längen
der Abschnitte auf der einen Halbgeraden,
wie die Längen der Abschnitte auf der anderen Halbgeraden.
Mit den Bezeichnungen in der Abbildung
ergibt sich:
|ZA‘|  |ZA|  |ZB‘|  |ZB|
Beweis
Da AB || A‘B‘ folgt mit Definition 5.2: A‘  ZZ, k(A)  B‘  ZZ, k(B)
Mit Satz 5.3 ergibt sich: |ZA‘|  |k|  |ZA|  |ZB‘|  |k|  |ZB|
Damit ergibt sich: |ZA‘|  |ZA|  |k|  |ZB‘|  |ZB|
#
Jürgen Roth
Geometrie
5.13
Folgerungen aus Satz 5.3
Satz 5.5: Zweiter Strahlensatz
Werden zwei von einem Punkt ausgehende Halbgeraden (oder deren
entgegengesetzte Halbgeraden) von
parallelen Geraden geschnitten, dann
verhalten sich die Längen der Abschnitte
auf den Parallelen wie die Längen der
Abschnitte auf einer Halbgeraden.
Mit den Bezeichnungen in der Abbildung
ergibt sich:
|A‘B‘|  |AB|  |ZA‘|  |ZA|
Beweis
Da AB || A‘B‘ folgt mit Definition 5.2: A‘  ZZ, k(A)  B‘  ZZ, k(B)
Mit Satz 5.3 ergibt sich: |A‘B‘|  |k|  |AB|  |ZA‘|  |k|  |ZA|
Damit ergibt sich: |A‘B‘|  |AB|  |k|  |ZA‘|  |ZA|
#
Jürgen Roth
Geometrie
5.14
Folgerungen aus Satz 5.3
Satz 5.6: Verhältnistreue der zentrischen Streckung
Das Längenverhältnis zweier Bildstrecken bei einer zentrischen
Streckung ist gleich dem Längenverhältnis ihrer Urbildstrecken.
Beweis
[AB] und [CD] sind Strecken und [A‘B‘] sowie [C‘D‘]
ihre Bildstrecken bei der zentrischen Streckung ZZ, k.
Mit Satz 5.3 ergibt sich: |A‘B‘|  |k|  |AB|  |C‘D‘|  |k|  |CD|
Damit ergibt sich:
|A‘B‘|  |C‘D‘|  (|k|  |AB|)  (|k|  |CD|)  |AB|  |CD|
#
Satz 5.7: Orientierungstreue der zentrischen Streckung
Bei einer zentrischen Streckung wird ein Dreieck auf
ein Dreieck mit gleicher Orientierung abgebildet.
Jürgen Roth
Geometrie
5.15
Folgerungen
Bemerkung
Da Dilatationen Geraden auf parallele Geraden abbilden,
sind sie geraden- und winkelmaßtreu. Folglich bilden alle
Dilatationen Dreiecke auf Dreiecke ab.
Beweisidee zu Satz 5.7
Es genügt den Fall k  0 zu betrachten,
da für k  0 die Situation mit einer
Punktspiegelung, die eine gleichsinnige Abbildung ist, auf den Fall
k  0 zurückgeführt werden kann.
Der Beweisgang lässt
sich aus der Abbildung
ablesen.
Jürgen Roth
Geometrie
5.16
Folgerungen
Satz 5.8: Änderung des Flächeninhalts bei zentrischer Streckung
Bei einer zentrischen Streckung ZZ, k wird der Flächeninhalt
eines Polygons auf das k2-fache vergrößert bzw. verkleinert.
Beweis
Da jedes einfach zusammenhängende Polygon trianguliert,
also in endlich viele Dreiecke zerlegt werden kann, genügt es,
den Satz für Dreiecke zu beweisen.
 ist ein Dreieck und ‘ sein Bilddreieck bei einer zentrischen
Streckung ZZ, k. Nach Satz 3.15 gilt dann:
A  ½  g  h
und
A‘  ½  g‘  h‘
Wegen g‘  ZZ, k(g) und h‘  ZZ, k(h) folgt mit Satz 5.3:
Also folgt:
Jürgen Roth
g‘  |k|  g und h‘  |k|  h
A‘  ½  g‘  h‘  ½  (|k|  g)  (|k|  h)
 |k|2  ½  g  h  k2  A
Geometrie
#
5.17
Folgerungen
Satz 5.9
Sind zwei parallele Pfeile AB und A‘B‘ gegeben, die nicht gleichzeitig
gleichorientiert und kongruent zueinander sind, dann gibt es genau
eine zentrische Streckung die AB auf A‘B‘ abbildet.
Satz 5.10
Wenn in zwei Dreiecken die Seiten auf paarweise parallelen Geraden
liegen, dann gibt es entweder genau eine zentrische Streckung oder
genau eine Parallelverschiebung, also genau eine Dilatation, die das
eine Dreieck auf das andere abbildet.
Man sagt: Die Dreiecke sind in perspektiver Lage.
Satz 5.11: Inverses einer zentrischen Streckung
Die zentrische Streckung ZZ, k ist eine bijektive Abbildung der Ebene 
auf sich. Die zu ZZ, k inverse Abbildung ist die zentrische Streckung
mit demselben Zentrum Z und dem Streckungsfaktor 1/k.
Jürgen Roth
Geometrie
5.18
Kapitel 5: Ähnlichkeitsabbildungen
5.2 Ähnlichkeitsabbildung –
Ähnlichkeit
Jürgen Roth
Geometrie
5.19
Ähnlichkeit
Jürgen Roth
Geometrie
5.20
Ähnlichkeitsabbildung
Definition 5.4
Eine Ähnlichkeitsabbildung ist die Verkettung einer endlichen
Anzahl von zentrischen Streckungen mit einer endlichen Anzahl
von Kongruenzabbildungen.
Definition 5.5
Eine Figur F1 heißt genau dann ähnlich zu einer Figur F2, wenn es
eine Ähnlichkeitsabbildung  gibt, die F1 auf F2 abbildet.
Satz 5.12: Eigenschaften von Ähnlichkeitsabbildungen
Ähnlichkeitsabbildungen sind geradentreu, winkelmaßtreu,
parallelentreu und verhältnistreu.
Satz 5.13: Eigenschaften von Ähnlichkeitsabbildungen
In ähnlichen Polygonen verhalten sich die Flächeninhalte
wie die Quadrate entsprechender Seitenlängen.
Jürgen Roth
Geometrie
5.21
Ähnlichkeitssätze für Dreiecke
Satz 5.14
Zur Verkettung  ∘ ZZ, k einer zentrischen Streckung ZZ, k mit einer
Kongruenzabbildung  gibt es immer eine Kongruenzabbildung *,
so dass gilt:
 ∘ ZZ, k  ZZ, k ∘ *
Satz 5.15: Ähnlichkeitsabbildungen
Jede Ähnlichkeitsabbildung lässt sich als Verkettung einer
Kongruenzabbildung und einer zentrischen Streckung darstellen.
Satz 5.16: Ähnlichkeitssatz „ww“ für Dreiecke
Sind zwei Winkel eines Dreiecks den entsprechenden Winkeln eines
anderen Dreiecks kongruent, dann sind die Dreiecke ähnlich.
Satz 5.17: Ähnlichkeitssatz 2 für Dreiecke
Stimmen zwei Dreiecke in den Verhältnissen der
drei Seitenlängen überein, dann sind sie ähnlich.
Jürgen Roth
Geometrie
5.22
Ähnlichkeitssätze für Dreiecke
Beweis zu Satz 5.16
Es sind zwei Dreiecke ABC und A1B1C1 gegeben, mit den
Maßzahlen der Seitenlängen a, b, c bzw. a1, b1, c1, für die gilt:
a b  a1 b1

b c  b1 c1
 a1 a  b1 b c1 c  k  0
 a1  k  a  b1  k  b  c1  k  c (*)
Mit A‘B‘C‘  ZZ, k(ABC) ergibt sich:
a‘  k  a  b‘  k  b  c‘  k  c
(*)
 a‘  a1  b‘  b1  c‘  c1
SSS
 A‘B‘C‘  A1B1C1
Nach Satz 2.1 gibt es folglich genau eine Kongruenzabbildung 
mit  (A‘B‘C‘)  A1B1C1.
 ∘ ZZ, k ist eine Ähnlichkeitsabbildung mit ( ∘ ZZ, k)(ABC)  A1B1C1,
also sind die Dreiecke ABC und A1B1C1 ähnlich.
#
Jürgen Roth
Geometrie
5.23
Ähnlichkeitsabbildungen
Satz 5.18
Eine Ähnlichkeitsabbildung ist durch drei nicht kollineare
Punkte und ihre Bildpunkte eindeutig bestimmt.
Beweisidee
Jürgen Roth
Geometrie
5.24
Drehstreckung
Definition 5.6
Eine Drehstreckung ist eine Verkettung
einer zentrischen Streckung und einer
Drehung mit demselben Zentrum.
Kurz:
DZ, , k  DZ,  ∘ ZZ, k
Z
Satz 5.19
Bei einer Drehstreckung DZ, , k sind die
Drehung und die zentrische Streckung,
aus denen sie sich zusammensetzt,
vertauschbar.
DZ, , k  DZ,  ∘ ZZ, k  ZZ, k ∘ DZ, 
Z
Jürgen Roth
Geometrie
5.25
Drehstreckung
Klappstreckung
Bemerkungen
Zentrische Streckungen sind spezielle Drehstreckungen mit dem
Winkelmaß   0°.
Drehungen sind Drehstreckungen mit dem Streckungsfaktor k  1.
Punktspiegelungen sind Drehstreckungen mit dem Streckungsfaktor k  1 (k  1) und dem Winkelmaß   0° (  180°).
Die identische Abbildung ist eine Drehstreckung
mit k  1 und   0°.
Das Zentrum Z ist für jede Drehstreckung, die nicht die Identität ist,
der einzige Fixpunkt.
Definition 5.7
Eine Klappstreckung (Streckspiegelung) ist eine Verkettung einer
zentrischen Streckung und einer Achsenspiegelung, deren Achse g
durch das Streckungszentrum Z verläuft.
Kurz:
KZ, k, g  Sg ∘ ZZ, k
Jürgen Roth
Geometrie
5.26
Klappstreckung
Bemerkungen
Geradenspiegelungen sind
Klappstreckungen mit dem
Streckungsfaktor k  1.
Bei Klappstreckungen
mit |k|  1 ist das
Streckungszentrum
der einzige Fixpunkt.
Z
Satz 5.20
Bei einer Klappstreckung KZ, k, g sind die Geradenspiegelung und
die zentrische Streckung, aus denen sie sich zusammensetzt,
miteinander vertauschbar.
KZ, k, g  Sg ∘ ZZ, k  ZZ, k ∘ Sg
Jürgen Roth
Geometrie
5.27
Abbildungstypen der
Ähnlichkeitsabbildungen
Bemerkung
Es gibt vier Abbildungstypen der Ähnlichkeitsabbildungen
Drehstreckung DZ, , k
[ Diese umfassen für   0° die
reinen Streckungen und für
k  1 die reinen Drehungen. ]
Parallelverschiebungen Tv
Klappstreckungen KZ, k, g [ Diese umfassen für k  1 die
reinen Geradenspiegelungen. ]
Gleitspiegelungen Gg, v
Satz 5.21: Typen von Ähnlichkeitsabbildungen
Eine Ähnlichkeitsabbildung ist eine Kongruenzabbildung,
eine Drehstreckung oder eine Klappstreckung.
Jürgen Roth
Geometrie
5.28
Gruppe der Ähnlichkeitsabbildungen
Bemerkung
Die Abbildung gibt einen
Überblick über die
Struktur der Gruppe der
Ähnlichkeitsabbildungen.
Nur die wichtigsten
Untergruppen werden
genannt.
Insbesondere zyklische
Untergruppen sind nur
zum Teil aufgenommen.
Kommutative Gruppen
sind durch (K)
gekennzeichnet.
Jürgen Roth
Geometrie
5.29
Seitenhalbierenden
eines Dreiecks
Definition 5.8
Eine Seitenhalbierende im Dreieck ist die Verbindungsstrecke eines
Eckpunkts mit dem Mittelpunkt der gegenüberliegenden Seite.
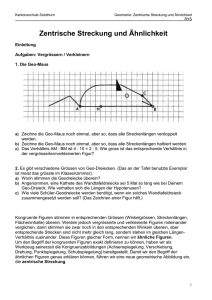
Satz 5.22: Seitenhalbierenden im Dreieck
Die Seitenhalbierenden eines Dreiecks schneiden sich in einem
Punkt S, der jede Seitenhalbierende in Verhältnis 21 teilt.
Beweis
Die Seiten des Dreiecks A‘B‘C‘ aus den Mittelpunkten
der Seiten von Dreieck ABC sind nach dem Satz über
die Mittelparallelen (Satz 2.39a) halb so lang und
„parallel“ zu den entsprechenden Seiten von ABC.
Sätze 5.3/5.10
 S ZS, ½(ABC)  A‘B‘C‘
 S  AA‘  BB‘ CC‘ (Schnittpunkt der Seitenhalbierenden)
Def 5.3
k = -1/2, Satz 5.3
 X{A, B, C} X-S-X‘  |X‘S|  |½|  |XS|
Jürgen Roth
Geometrie
 X{A, B, C} |XS|  |X‘S|  2  1
#
5.30