3. Ähnlichkeitsabbildungen

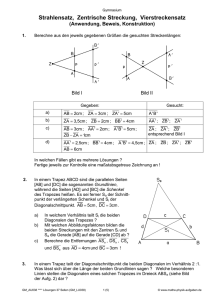
27
3.
Ähnlichkeitsabbildungen
3.1
Definitionen: Ähnlichkeitsabbildungen, Dilatationen
Bis jetzt haben wir Isometrien (Kongruenzabbildungen) betrachtet. Diese Abbildungen
wurden aufgebaut aus den Geradenspiegelungen.
Isometrien sind bijektive Abbildungen, die längentreu, geradentreu und winkeltreu sind.
Kongruente Figuren sind deckungsgleiche Figuren ( ! ).
Wir verzichten nun auf die Längentreue. Dies führt zu den Ähnlichkeitsabbildungen.
Definition: Eine geradentreue und winkeltreue, bijektive Abbildung der Ebene auf sich
heisst eine Ähnlichkeitsabbildung.
Die Bildfigur entsteht durch Vergrösserung des Urbildes (oder Verkleinerung).
Jede Strecke wird im gleichen Massstab verändert (z.B. verdoppelt).
Das Längenverhältnis zweier Strecken im Urbild und im Bild ist gleich.
Man schreibt für zwei ähnliche Figuren A und A‘ :
A ~ A‘.
Nun fordern wir zusätzlich, dass jede Gerade auf eine zu ihr parallele Geraden abgebildet
wird. Eine solche Abbildung nennt man Dilatation.
Definition
Eine bijektive Abbildung der Ebene auf sich heisst Dilatation, wenn sie jede Gerade auf
eine zu ihr parallele Gerade abbildet.
!
g
UNIZH MA430 Geom 1 J.S-D
g'
28
Eigenschaften der Dilatationen
•
Die Dilatationen sind winkeltreu, also Ähnlichkeitsabbildungen.
!
!
g
h
g’ || g
•
Die Translationen sind Dilatationen. Sie sind die einzigen Dilatationen ohne Fixpunkt.
(Eigenschaft 6 der Translationen, Seite 22)
! Translation (" id)
•
h’ || h
#
! Dilatation ohne Fixpunkt
Bei einer Dilatation mit Fixpunkt ist jede Gerade durch einen Fixpunkt eine Fixgerade.
g = g’
S
•
Eine von der Identität verschiedene Dilatation hat höchstens einen Fixpunkt.
Eine Dilatation mit genau einem Fixpunkt S heisst zentrische Streckung.
Beweis?
UNIZH MA430 Geom 1 J.S-D
29
3.2
Zentrische Streckung
Definition
Eine Dilatation mit genau einem Fixpunkt S heisst zentrische Streckung. Der Fixpunkt S
heisst Streckzentrum.
Die zentrischen Streckungen sind ausser der Identität die einzigen Dilatationen mit Fixpunkt.
Abbildung eines Dreiecks durch eine zentrische Streckung mit Zentrum S:
C
C‘
S
B
A
B‘
A’
Eigenschaften der zentrischen Streckung
1. Bei einer zentrischen Streckung mit dem Zentrum S liegen ein beliebiger Punkt P (≠S)
und sein Bild P' auf einer Geraden durch den Fixpunkt S.
2. Bei einer zentrischen Streckung wird jede Gerade g, die nicht durch das Zentrum S geht,
auf eine von g verschiedene Parallele abgebildet.
Bemerkung
Eine zentrische Streckung ist durch ihr Zentrum S und durch einen von S verschiedenen
Punkt A und sein Bild A' eindeutig festgelegt.
UNIZH MA430 Geom 1 J.S-D
30
Satz 1: Bei einer zentrische Streckung mit dem Zentrum S gilt für jeden Punkt A und sein
Bild A'
!!!"
!!"
SA' = k !SA
wobei k (≠ 0) eine feste reelle Zahl ist. k heisst Streckfaktor.
Bezeichnung: zentrische Streckung mit Streckzentrum S und Streckfaktor k:
Z
Sk
'
Bemerkung
| k | > 1: Vergrösserung der Entfernung von S
| k | < 1: Verkleinerung der Entfernung von S
k > 0: Urbild und Bild liegen auf derselben Seite von S
k < 0: Urbild und Bild liegen auf entgegengesetzten Seiten von S
Beweis von Satz 1: Untersuchung der Längenverhältnisse
!!" !!!"
1. Wir wählen einen beliebigen Punkt P, sein Bild sei P’. Die Vektoren SP, SP ' seien
!!!"
!!"
gleichgerichtet und SP ' = k SP , wobei k !#, k > 0
k=
m
, m, n !!
n
!!" !!"
Nun wählen wir den Punkt E, so dass gilt: nSE = SP
!!!"
!!" m !!"
!!"
Damit wird
SP ' = kSP = nSE = mSE
n
g
P’
P
E
S
F
Q
Q’
h
UNIZH MA430 Geom 1 J.S-D
31
Liegt der Punkt Q nicht auf der Geraden g durch S und P und ist h die Gerade durch S und
Q, so schneiden die Parallelen zu PQ durch alle Teilpunkte von g auf der Geraden h
kongruente Teilstrecken aus.
!!"
!!"
Der Vektor SE auf g entspricht dem Vektor SF auf h und es gilt:
!!"
!!"
!!!" m !!"
!!"
SB = nSF !#
!!!"
!!" " % SB' = SB = kSB
n
SB' = mSF $#
Liegt der Punkt R auf der Geraden g, so kann jetzt wie vorher, aber von der Geraden h aus
argumentiert werden.
Ist k !! irrational, dann muss die irrationale Zahl durch rationale Zahlen ( z.B. mit
Intervallschachtelungen) approximiert werden.
!!" !!!"
2. Sind die Vektoren SP, SP ' parallel, aber entgegengesetzt, also k < 0, dann spiegelt man
zuerst A’ an S, ergibt A* und folgert wie bei 1.
A
A*
!!!"
!!"
SA' == kSA, k < 0
!!!!"
!!"
SA * = !kSA
S
A’
!!!" "
3. Ist k = 0, also SA' = 0 , dann wird jeder Punkt auf S abgebildet. Diese Abbildung ist aber
nicht injektiv!
Ende Beweis
Auch die Umkehrung von Satz 1 ist richtig. Damit kann man eine zur Definition der
zentrischen Streckung äquivalente Definition angeben.
Satz 2:
Eine Abbildung ϕ = Z
Jedem Punkt A wird ein
Sk
'
der Ebene auf sich ist eine
zentrische Streckung mit
Zentrum S und Streckfaktor k
Verallgemeinern wir nun Satz 1, dann gilt:
UNIZH MA430 Geom 1 J.S-D
Punkt A' so zugeordnet, dass
⇔
A und A' auf einer Geraden
durch S liegen und dass gilt:
!!!"
!!"
SA' = k !SA .
32
Satz 3:
Bildet die zentrische Streckung Z
A auf A' und B auf B' ab, dann gilt für die
Sk
'
!!!!"
!!!"
Vektoren: A' B' = k ! AB
Das Bild einer Strecke hat also die |k| - fache Länge der Urbildstrecke.
B’
B
S
A
A‘
Bemerkungen
k = 1:
Die Identität ist ein Spezialfall einer zentrischen Streckung.
k = -1:
Die Punktspiegelung ist auch eine spezielle zentrische Streckung.
Die Sätze 2 und 3 sind gleichbedeutend mit den Strahlensätzen.
1. Strahlensatz
Werden zwei von einem Punkt ausgehende Strahlen (oder deren entgegengesetzte
Strahlen) von parallelen Geraden geschnitten, so verhalten sich die Längen der
Abschnitte auf dem einen Strahl wie die Längen der entsprechenden Abschnitte auf
dem anderen Strahl.
| SA! | | SB! | | k |
=
=
| SA | | SB |
1
B'
A'
B
S
S
A
A'
UNIZH MA430 Geom 1 J.S-D
B'
B
A
33
2. Strahlensatz
Werden zwei von einem Punkt ausgehende Strahlen von zwei Parallelen
geschnitten, so verhalten sich die Längen der Abschnitte auf den Parallelen wie die
der zugehörigen Scheitelabschnitte auf einem Strahl.
| A' B'| | SA'|
=
=|k|
| AB | | SA |
Weitere Eigenschaften der zentrischen Streckung Z
Sk
'
•
Das Längenverhältnis zweier Bildstrecken ist gleich dem Längenverhältnis ihrer
Urbildstrecken.
•
Ein Dreieck und sein Bild haben dieselbe Orientierung.
•
Die Flächeninhalte von Bild und Urbild verhalten sich wie
•
Die zur zentrischen Streckung Z
Sk
'
den Streckfaktor
1
.
k
k2
.
1
inverse Abbildung hat dasselbe Streckzentrum und
!1
(ZS,k ) = ZS,1k
Die Eigenschaft c) überlegt man sich zuerst für Dreiecke. Dann betrachtet man Polygone
(geschlossene Streckenzüge), die man vollständig mit Dreiecken ausschöpfen kann.
Schliesslich können krummlinig begrenzte Figuren durch Dreiecke beliebig genau
approximiert werden.
Beispiele
1. In ein Dreieck ABC soll ein Quadrat PQRS mit P, Q ∈ AB, R ∈ BC, S ∈ AC
eingezeichnet werden.
2. Konstruiere durch den Schnittpunkt S zweier Kreise k und k eine Sekante, sodass die
1
beiden auf ihr liegenden Sehnen sich wie 2 :3 verhalten.
UNIZH MA430 Geom 1 J.S-D
2
34
3.3
Harmonische Teilung und Apolloniuskreis
Gegeben ist eine Strecke AB (B ≠ A) und ein Streckfaktor k (≠ 1). Wo liegt das
Streckzentrum S?
!!"
!!"
SB = k ! SA
Es gilt:
!!!"
!!!"
S1 B = k1 S1 A
k >0:
1
S1
A
!!!"
!!!"
S2 B = k2 S2 A
k <0:
2
B
A
S2
S heisst äusserer Teilpunkt
B
S heisst innerer Teilpunkt
1
2
Definition
Ist | k | = k = k (> 0), so wird die Strecke AB durch die Punkte S und S
2
1
1
2
harmonisch geteilt.
AS1
BS1
=
AS2
BS2
=k
Die Konstruktionsideen werden durch folgende Beispiele klar.
1. Beispiel: Die Strecke AB soll harmonisch im Verhältnis 2 : 3 geteilt werden.
A
B
2. Beispiel: Kennt man die Strecke AB und einen Teilpunkt S, so ist der andere Teilpunkt T
eindeutig bestimmt.
A
UNIZH MA430 Geom 1 J.S-D
S
B
Satz 4:
35
Teilen die Punkte S und T die Strecke AB harmonisch im Verhältnis k, so teilen
die Punkte A und B die Strecke ST auch harmonisch, und zwar im Verhältnis
k +1
.
!=
k "1
(Beweis in der nächsten Uebungsserie!)
Wir zeichnen im Dreieck ABC die Winkelhalbierende von γ. Diese schneidet die
gegenüberliegende Seite AB = c im Punkt D. Warum gilt folgender Satz?
Satz 5:
In einem Dreieck teilt die Winkelhalbierende eines Innenwinkels die
gegenüberliegende Seite im Verhältnis der anliegenden Seiten.
C
Äussere Winkelhalbierende
wγ’
T
b
A
a
c
D
B
a
E
Innerere Winkelhalbierende
Satz 5':
wγ
Ist das Dreieck nicht gleichschenklig, so teilt auch die Winkelhalbierende des
Aussenwinkels die gegenüberliegende Seite im Verhältnis der anliegenden
Seiten.
Damit erhalten wir den berühmten Satz des Apollonius.
UNIZH MA430 Geom 1 J.S-D
36
Satz 6:
Kreis des Apollonius
Die Menge aller Punkte, für die das Abstandsverhältnis zu zwei festen Punkten
A und B den konstanten Wert k annimmt, ist der Kreis mit dem Durchmesser
ST, wobei S und T die Strecke AB harmonisch im Verhältnis k teilen.
C
b
a
A
S
B
M
3. Beispiel: Konstruieren Sie ein Dreieck aus den Seiten b = 6, c = 3 und der
Winkelhalbierenden w! = 3.5.
UNIZH MA430 Geom 1 J.S-D
T
37
Satz 7:
Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt S, der jede
Seitenhalbierende innen im Verhältnis 2:1 teilt.
S heisst der Schwerpunkt des Dreiecks.
C
A'
B'
S
B
C'
A
Satz 8: In einem Dreieck schneiden sich die drei Winkelhalbierenden in einem Punkt.
C
wβ
wα
W
b
a
A
B
wγ
UNIZH MA430 Geom 1 J.S-D
38
3.4
Verschiedene Ähnlichkeitsabbildungen
3.41
Ähnlichkeitsabbildungen allgemein
Satz 9:
Eine Ähnlichkeitsabbildung ϑ ist durch drei nicht kollineare Punkte und ihre
Bildpunkte eindeutig bestimmt.
ϑ:
A → A'
B → B'
C → C'
a) Zwei Dreiecke sind genau dann ähnlich, wenn zwei Winkel des einen
Dreiecks gleich den entsprechenden Winkeln des anderen Dreiecks sind.
b) Zwei Dreiecke sind genau dann ähnlich, wenn sie in den Verhältnissen der
drei Seitenlängen übereinstimmen.
a a' a a'
= ,
= , ! = !' , " = "' , # = # ' .
b b' c c'
C’
b’
C
α
A
Satz 10:
A’
γ
b
β
c
a
α’
γ’
a’
c
B
β’
B’
Eine Abbildung ist genau dann eine Ähnlichkeitsabbildung ϑ, wenn sie
darstellbar ist als Verknüpfung einer Isometrie ϕ und einer zentrischen
Streckungen Z .
Sk
'
! Ähnlichkeitsabbildung
"
! = Z S, k ! #
Beweis:
"!":
Ist ϕ eine Isometrie und ZS,k eine zentrische Streckung, so ist die Verknüpfung der
beiden Abbildungen eine Ähnlichkeitsabbildung.
"!":
Ist ϑ eine Ähnlichkeitsabbildung, dann ist sie durch 3 nicht kollineare Punkte und
ihre Bilder eindeutig bestimmt.
! :!ABC "!A' B'C '
UNIZH MA430 Geom 1 J.S-D
39
Man kann die Abbildung zum Beispiel zerlegen in eine Translation gefolgt von
einer Rotation und einer zentrischen Streckung.
"""#
! = Z A ', k ! RA ', µ ! T"AA
'
C’
C2
B’
C1
B2
µ
A’
C
B1
! """!
v = AA'
A
UNIZH MA430 Geom 1 J.S-D
B
40
3.42
Drehstreckungen und Klappstreckungen
Definition
Eine Drehstreckung ist die Verknüpfung einer zentrischen Streckung und einer Rotation
mit demselben Zentrum
! = RS," ! Z S, k
Es gilt:
! = RS," ! Z S, k = Z S, k ! RS,"
Spezielle Drehstreckungen:
i)
α = 0°: zentrische Streckung
ii)
k = 1: Rotation
RS,0 ! Z S.k = Z S, k
RS,! ! Z S,1 = RS,!
k = 1, α = 0°: Identität
iii)
RS,0 ! Z S,1 = id
•
Eine Drehstreckung, die nicht die Identität ist, hat genau einen Fixpunkt.
•
Bei Drehstreckungen genügt es, positive k zu betrachten, denn
! = RS," ! Z S, k = RS," +180° ! Z S,# k
UNIZH MA430 Geom 1 J.S-D
41
Definition
Eine Klappstreckung ist die Verknüpfung einer zentrischen Streckung und einer
Geradenspiegelung, deren Achse durch das Streckzentrum geht.
! = Sg ! Z S, k
! = Sg ! Z S, k = Z S, k ! Sg
Es gilt:
Spezielle Klappstreckung: k = 1: Geradenspiegelung
•
Sg ! Z S,1 = Sg
Eine Klappstreckung mit |k| ≠ 1 hat genau einen Fixpunkt.
Satz 11:
Die Verknüpfung einer gleichsinnigen Isometrie und einer zentrischen Streckung
(k ≠ 1) ist eine Drehstreckung.
Die Verknüpfung einer ungleichsinnigen Isometrie und einer zentrischen
Streckung (k ≠ 1) ist eine Klappstreckung.
UNIZH MA430 Geom 1 J.S-D
42
Satz 12:
Die Verknüpfung zweier zentrischer Streckungen Z S2 , k2 ! Z S1 , k1 mit
verschiedenen Zentren S1 ≠ S2 und k = k2 ! k1 ist:
a) eine zentrische Streckung ZS,k,
falls k ≠ 1, und einem Zentrum S, das auf der Geraden S1S2 liegt.
!!!" 1 ! k2 !!!!"
Für die Lage von S gilt:
S1S =
S1S2
1 ! k1k2
!
b) eine Translation Tv! , falls k = 1, wobei v parallel zur Geraden S1S2 ist
und
Satz 13:
""""!
!
v = (1 ! k2 )S1S2
Gegeben sind eine Translation Tv! und eine zentrische Streckung Z S, k (k ! 1) .
Dann ist die Verknüpfung wieder eine zentrische Streckung.
####"
Z S, k ! Tv" = Z S*, k , wobei SS * =
UNIZH MA430 Geom 1 J.S-D
k "
v.
1! k