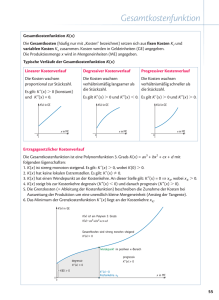
Kapitel 10 Kostenfunktionen Ökonomische Kosten Ökonomische

Kostenfunktionen
• Kosten der Produktion für eine gegebene Outputmenge.
– Lösung des Kostenminimierungsproblems
Kapitel 10
• Gesamt-, Grenz- und Durchschnittskosten.
Kostenfunktionen
• Kurzfristige und langfristige Kostenkurven.
1
Ökonomische Kosten
2
Ökonomische Kosten
Die Opportunitätskosten
• Beim Messen der Kosten für den Gebrauch eines Inputs
bedienen
sich
Ökonomen
des
Konzepts
der
Opportunitätskosten: Der Wert des Inputs beim Einsatz in
der besten Alternative.
• Buchhalterische Kosten: Der tatsächliche Buchwert der
Ausgaben für Anlagegüter.
Beispiel: Die Kosten von Arbeit. Wenn Arbeit auf einem
vollkommenen Wettbewerbsmarkt zum Preis w angeboten
und nachgefragt wird, dann ist w auch gleich den
Opportunitätskosten, also dem Preis, den der Arbeiter bei
einem anderen Arbeitgeber bekommen hätte. In diesem Fall
stimmen ökonomische und buchhalterische Kosten überein.
3
Kosten der Kapitalausgaben: Die Opportunitätskosten
der Maschine, die sich aus ihrer besten alternativen
Verwendungsmöglichkeit in der Produktion ergibt.
Der Mietzins von Kapital (rental rate of capital): Der „Preis“,
den eine andere Partei bereit ist, für die Maschine (in
einer Periode) zu zahlen.
Buchhalterische Kapitalausgaben: Die tatsächlichen
Ausgaben werden als Aktivposten gebucht, dann wird
der Buchwert des Kapitals über die Zeit abgeschrieben.
4
Versunkene Kosten
Kostenminimierung
• Versunkenen Kosten (Sunk Costs) sind die Ausgaben,
die getätigt worden sind und nicht mehr rückgängig
gemacht werden können.
Kostenminimierung:
• Ziel: Finde die minimalen Kosten, die zur Produktion einer
vorgegebenen Menge des Gutes notwendig sind.
• Wenn wir die Preise/Schattenpreise für jedes Input kennen, können
wir die Gesamtausgaben angeben mit w, dem Preis für Arbeit (wage
rate) und v, dem Mietpreis für Kapital (Zins). Dann:
• Derartige Kosten sollten die Entscheidung
Unternehmens nicht beeinflussen.
eines
C  wL  vK
•
Um die Produktionskosten zu finden, formulieren wir das
Optimierungsproblem mit Nebenbedingung: Minimiere die Ausgaben
unter der Bedingung, dass mindestens eine bestimmte Outputmenge
Q produziert wird.
5
6
Kostenminimierung
Kostenminimierung
Graphische Darstellung:
RTS K , L 
•
•
Kostenminimierung:
minwL  vK  u.d .N . Q  F ( K , L)
FK ( K , L) v

FL ( K , L) w
L( K , L,  )  wL  vK   (Q  F ( K , L))
Lagrange:
Grenzrate der technischen
Substitution ist gleich dem
Preisverhältnis der Inputs.
BoOs: L( K , L,  )  w  F ( K , L)  0
L
L
L( K , L,  )
 v  FK ( K , L)  0
K
L( K , L,  )
 Q  F ( K , L)  0

Das Grenzprodukt eines Euros
ist für jeden Faktor gleich.
Finde:
FK ( K , L) FL ( K , L)

v
w
7
RTS K , L 
FK ( K , L) v

FL ( K , L) w
8
Kostenminimierung
Beispiel:
• Angenommen Toyota‘s Produktionstechnologie für Autos ist
Kostenfunktionen
Lösung des Kostenminimierungsproblems:
Q  K L
•
Falls w=20 und v=5, was sind die minimalen Kosten um 10 Autos zu produzieren?
•
Lagrange:
•
BeOs:
•
Inputnachfragen als Funktion der Outputproduktion:
K (v, w, Q) und L(v, w, Q)
•
C (v, w, Q)  vK (v, w, Q)  wL(v, w, Q)
•
•
Gesamtkostenfunktion:
Die Gesamtkosten zur Produktion von Q Einheiten Output ist eine
Funktion von Q und den Inputpreisen.
Lösung bei diesen Werten:
9
Kostenfunktionen
10
Kostenfunktionen
• Gesamtkosten C(Q) (manchmal TC(Q)), gegeben aus der
Kostenminimierung. Die monetären Kosten, einen gegebenen
Output Q zu produzieren.
Beispiel:
Im Toyota Beispiel ist die Gesamtkostenfunktion:
• Eigenschaften der Gesamtkostenfunktion:
Die Grenzkosten:
– Homogen vom Grad 1 in den Inputpreisen.
– Nicht-fallend in Q,v,w.
– Konkav in den Inputpreisen.
Die Durchschnittskosten:
• Grenzkosten MC(Q)=dC/dq, die Ableitung von C(Q) nach Q
misst die Grenzkosten einer zusätzlichen Outputeinheit.
• Durchschnittskosten AC(Q)=C(Q)/Q, Kosten pro Outputeinheit.
11
12
Kostenfunktionen
Kostenfunktionen
Skalenerträge und die Kostenfunktion:
• Wenn F(K,L) konstante Skalenerträge hat,
Gesamtkostenfunktion linear in Q.
• Wenn F(K,L) steigende Skalenerträge hat,
Gesamtkostenfunktion steigend und konkav
Grenzkostenfunktion fallend.
• Wenn F(K,L) fallende Skalenerträge hat,
Gesamtkostenfunktion steigend und konvex
Grenzkostenfunktion steigend.
Beispiel: Allgemeine Cobb-Douglas Technologie F(K,L)=KαLβ
ist die
BeO‘s der Kostenminimierung:
ist die
und die
ist die
und die
Lösung der BeO‘s:
• Beispiel: Die Gesamtkosten bei Toyota sind linear in Q,
also hat die Produktionstechnologie konstante
Skalenerträge.
13
14
Kostenfunktionen
Kurz- und langfristige Kosten
Die Cobb-Douglas Gesamtkostenfunktion:
Fixe vs. variable Inputs:
•
Langfristig sind alle Inputs variabel.
•
Kurzfristig sind einige Inputs fix.
–
–
MC:
AC:
•
RTS hängt von den Exponenten ab. Diese bestimmen
ebenfalls die Form der marginalen Kosten.
15
Maschinen
Arbeiter, wenn zusätzliche Arbeiter und Überstunden
unverhältnismäßig teuer sind.
Kurzfristige Kostenminimierung nimmt die fixen Inputs
als gegeben an und maximiert bezüglich der variablen
Faktoren.
16
Kurz- und langfristige Kosten
Kurz- und langfristige Kosten
Beispiel:
Angenommen, Toyota‘s Kapitalstock is kurzfristig bei K* fixiert.
• Die kurzfristigen Gesamtkosten werden durch flexibles L
bestimmt, um Q zu produzieren.
• Die notwendige Arbeit, um Q zu produzieren, ist:
Beispiel:
• Variable Kosten:
Die kurzfristigen Durchschnittskosten: SRAC  SRTC 
• Fixkosten von Kapital:
In der kurzen Frist sind die Durchschnittskosten U-förmig. Grenzkosten
steigen stärker als in der langen Frist.
Die kurzfristigen Gesamtkosten: SRTC (v, w, Q ) 
Die kurzfristigen Grenzkosten: SRMC 
SRTC

Q
Q
• Gesamtkosten: SRTC(v,w,Q)=
17
18
Kapitel 10 Konzepte
Kurz- und langfristige Kosten
• Opportunitätskosten
• Versunkene Kosten
• Gesamt-, Grenz- und
Durchschnittskosten
• Cobb-Douglas Kostenfunktion
• Kurzfristige Gesamt-, Grenzund Durchschnittskosten
Für das Toyota Beispiel:
19
20