1. Die reellen Zahlen Definition 1.1 (Verkettung). Die Verkettung

1. Die reellen Zahlen
Definition 1.1 (Verkettung). Die Verkettung oder Komposition der Abbildungen f : P → N und g : M → P ist die Abbildung f ◦ g : M →
N, x 7→ f (g(x)). Falls Definitionsbereich und Wertebereich gleich sind (also f : M → M ) schreiben wir auch f 2 statt f ◦ f . Die Abbildung
idM : M → M , x 7→ x ist die identische Abbildung (auf der Menge M ).
Definition 1.2 (Multiplikation und Addition für reelle Funktionen). Es sei M ⊂ R. Es seien f : M → R und g : M → R reelle Funktionen,
dann nennen wir die Funktion f + g : M → R, x 7→ f (x) + g(x) Summe von f und g, und f · g : M → R, x 7→ f (x)g(x) das Produkt von f und
g.
Die Axiome der rellen Zahlen: Die Menge R versehen mit der Addition + : R × R → R und der Multiplikation · : R → R erfülle
das Das Körperaxiom, das Axiom der Anordnung und das Vollständigkeitsaxiom.
1: Das Körperaxiom: R ist bezüglich Addition und Multiplikation ein Körper.
2: Die Anordnungsaxiom: Es gibt eine Teilmenge R+ ⊂ R mit den Eigenschaften:
A1: Für jedes x ∈ R gilt genau einer der Aussagen: x ∈ R+ , −x ∈ R+ bzw. x = 0.
A2: Sind x, y ∈ R+ so folgt x + y ∈ R+ .
A3: Sind x, y ∈ R+ so folgt xy ∈ R+ .
Die Menge R+ nennen wir die Menge der positiven Zahlen. Die Menge R− := {x ∈ R | − x ∈ R+ } nennen wir die Menge der negativen
Zahlen. Wir definieren x < y :⇔ y − x ∈ R+ und x ≤ y :⇔ y − x ∈ R+ ∪ {0}
Satz 1.3. Die Relation ≤ ist eine Ordnungsrelation, d.h. es gilt:
i) Für alle x ∈ R gilt x ≤ x (Reflexivität)
ii) Aus x ≤ y und y ≤ z folgt x ≤ z (Transitivität)
iii) Aus x ≤ y und y ≤ x folgt x = y (Antisymmetrie)
Definition 1.4 (Beschränkte Mengen).
a) Eine Menge M ⊂ R heißt beschränkt, falls es eine Zahl Z ∈ R gibt, so dass |m| ≤ Z für
jedes m ∈ M gilt.
b) Eine Menge heißt von oben beschränkt, falls es eine Zahl Z ∈ R gibt, so dass m ≤ Z für jedes m ∈ M gilt. Ein solche Zahl Z
heißt obere Schranke von M .
c) Eine Menge heißt von unten beschränkt, falls es eine Zahl Z ∈ R gibt, so dass Z ≤ m für jedes m ∈ M gilt. Ein solche Zahl Z
heißt untere Schranke von M .
Definition 1.5 (Supremum, Infimum, Maximum, Minimum). Es sei M eine Teilmenge von R.
a)
b)
c)
d)
Die
Die
Hat
Hat
kleinste obere Schranke von M heißt Supremum.
größte untere Schranke von M heißt Infimum.
M ein Supremum, so heißt dieses Maximum, falls es ein Element der Menge M ist.
M ein Infimum, so heißt dieses Minimum, falls es ein Element der Menge M ist.
3: Das Vollständigkeitsaxiom (Supremumseigenschaft): Jede von oben beschränkte nichtleere Menge besitzt ein
Supremum.
Satz 1.6 (Das Archimedische Prinzip). Sind a, b ∈ R und b > 0 so gibt es ein n ∈ N, so dass nb > a.
Definition 1.7 (Topologische Eigenschaften von Teilmengen in R). Eine Teilmenge M heißt
a) offen in R falls es zu jedem m ∈ M ein > 0 gibt, so dass das Intervall ]m − , m + [ eine Teilmenge von M ist;
b) abgeschlossen, falls R \ M offen in R ist;
c) dicht in R falls zu jedem x ∈ R \ M und für jedes > 0 ein m ∈ M im Intervall ]x − , x + [ liegt.
Satz 1.8 (Dichtheit von Q in R). . a) Q liegt dicht in R. b) R \ Q liegt dicht in R.
Korollar 1.9.
a) Zwischen je zwei rationalen Zahlen gibt es irrationale Zahlen. Zwischen je zwei irrationalen Zahlen gibt es rationale
Zahlen.
b) Jede irrationale Zahl lässt sich mit rationalen Zahlen approximieren.
c) Q ist weder offen noch abgeschlossen in R.
Satz 1.10 (Kardinalität von Q und R). . a) Q ist abzählbar. b) R ist nicht abzählbar. c) R \ Q ist nicht abzählbar.
Lemma 1.11. Abzählbare Vereinigungen abzählbarer Mengen sind abzählbar.
2. Folgen und Reihen
Definition 2.1 (Folgen). Eine Abbildung a : N → R (bzw. a : N0 → R) nennt man Folge. Statt a : N → R schreibt man meist (an )n∈N und
an statt a(n).
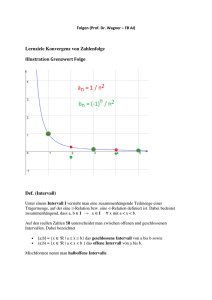
Definition 2.2 (Konvergenz, Divergenz, Grenzwert einer Folge). Es sei (an )n∈N eine Folge.
a) (an )n∈N heißt konvergent falls ein a ∈ R mit folgender Eigenschaft existiert: Zu jedem > 0 gibt es ein N ∈ N, so dass für alle
n > N die Ungleichung |an − a| < gilt. Der Wert a heißt in diesem Fall Grenzwert von (an )n∈N . Wir schreiben auch an → a
P
P∞
Pn
n→∞
für n → ∞ oder limn→∞ an = a oder an −→ a. Ist an = n
k=1 bn so schreiben wir auch
k=1 bk = a statt limn→∞
k=1 bn = a.
b) Eine Folge heißt divergent falls sie nicht konvergent ist.
c) Gibt es zu jedem K ∈ R ein N ∈ N mit an > K für alle n > N so schreiben wir limn→∞ an = ∞. Gibt es zu jedem K ∈ R ein
N ∈ N mit an < K für alle n > N so schreiben wir limn→∞ an = −∞.
Satz 2.3 (Eigenschaften von Grenzwerten). .
a) Jede Folge hat höchstens einen grenzwert (d.h. konvergiert die Folge (an )n∈N gegen a und gegen b so ist a = b.
b) Ist die Folge (an )n∈N konvergent so ist die Folge beschränkt, d.h., die Menge {an | n ∈ N} ist beschränkt.
c) Es seien (an )n∈N und (bn )n∈N konvergente Folgen mit limn→∞ an = a und limn→∞ bn = b.
(i) Seien α, β reelle Zahlen. Die Folge (αan + βbn )n∈N konvergiert gegen αa + βb. Die Menge der konvergenten Folgen bildet also
einen Unterraum von Abb(N, R) := {f : N → R}.
(ii) Die Folge (an bn )n∈N konvergiert gegen ab.
−1
(iii) ist bn 6= 0 für alle n ∈ N so konvergiert (b−1
.
n )n∈N gegen b
(iv) Gilt an < bn für alle bis auf endlich viele n ∈ N so ist a ≤ b.
(v) Ist (cn )n∈N eine Folge mit an ≤ cn ≤ bn und ist a = b so konvergiert (cn )n∈N gegen a.
Definition 2.4 (Häufungspunkte und Teilfolgen). Es sei (an )n∈N eine Folge.
a) Ist f : N → N streng monoton steigend, so nennt man die Folge (af (n) )n∈N eine Teilfolge von (an )n∈N .
b) Konvergiert eine Teilfolge (af (n) )n∈N gegen a ∈ R so nennt man a einen Häufungspunkt von (an )n∈N .
Satz 2.5 (Monotone Konvergenz). Ist (an )n∈N monoton steigend (fallend) und von oben (von unten) beschränkt so ist sie konvergent.
Satz 2.6 (Bolzano-Weierstraß). Jede beschränkte Folge hat eine konvergente Teilfolge.
Lemma 2.7 (Bernoulli Ungleichung). Für alle x ≥ −1 und alle n ∈ N gilt 1 + nx ≤ (1 + x)n .
Lemma 2.8 (Die Folge q n ). Sei q ∈ R. Die durch an = q n definierte Folge konvergiert genau dann wenn −1 < q ≤ 1.
P∞ n
Satz 2.9 (Geometrische Reihe). Sei q ∈ R. Die geometrische Reihe
konvergiert genau dann, wenn −1 < q < 1. Ist die Reihe
n=0 q
1
konvergent, dann konvergiert sie gegen 1−q
Definition 2.10 (Cauchy Folgen). Eine Folge (an )n∈N heißt Cauchy-Folge falls es zu jedem > 0 ein N ∈ N gibt, so dass für alle n, m ≥ N
die Abschätzung |an − am | < gilt.
Satz 2.11 (Cauchy-Konvergenzkriterium). Eine Folge ist genau dann konvergent, wenn Sie eine Cauchy-Folge ist.
P
Satz 2.12 (Notwendiges Konvergenzkriterium). Ist die Reihe ∞
k=1 ak konvergent so gilt limk→∞ ak = 0.
P
Lemma 2.13 (Verdichtungslemma von Cauchy). Sei (cn )n∈N eine nicht negative reelle monoton fallende Folge. Die Reihe ∞
n=1 cn konvergiert
P∞ k
genau dann wenn die Reihe k=1 2 c2k konvergiert.
P
1
Satz 2.14 (Harmonische Reihe). Sei α ∈ R. Die Reihe ∞
k=1 kα konvergiert genau dann, wenn α > 1. Insbesondere divergiert die HarmoP∞ 1
nische Reihe k=1 k .
P
1
Satz 2.15.
a) Die durch an = n
k=0 k! definierte Folge konvergiert.
1 n
b) Die durch bn = 1 + n
definierte Folge konvergiert.
c) Es gilt limn→∞ an = limn→∞ bn .
Definition 2.16. Die Zahl e := limn→∞ an = limn→∞ bn heißt Eulersche Konstante.
Satz 2.17. e ∈ R \ Q.
P
k
Satz 2.18 (Das Leibnizkriterium). Ist (ck )k∈N0 eine monoton fallende Nullfolge, so ist die Reihe ∞
k=0 (−1) ck konvergent.
P∞
P∞
Definition 2.19 (Absolute Konvergenz). Eine Reihe k=0 ak heißt absolut konvergent, falls die Reihe k=0 |ak | konvergiert.
P
Satz 2.20 (Absolute Konvergenz impliziert Konvergenz). Jede absolut konvergente Reihe ∞
k=0 ak ist konvergent. Für die Werte der Reihe
gilt die Ungleichung:
∞
∞
X X
ak ≤
|ak |
k=0
k=0
P
P∞
Satz 2.21 (Majoranten und Minoranten). Es sei ∞
k=0 ak eine Reihe und
k=0 ck eine Reihe mit ck ≥ 0 für alle k ∈ N.
P∞
P
a) Ist k=0 ck konvergent und gilt |ak | ≤ ck für alle (bis auf endlich viele) k ∈ N so ist ∞
a absolut konvergent.
P∞
P∞k=0 k
b) Ist k=0 ck divergent und gilt |ak | ≥ ck für alle (bis auf endlich viele) k ∈ N so ist k=0 |ak | divergent.
P
Satz 2.22 (Wurzelkriterium). Es sei ∞
k=0 ak eine Reihe.
p
a) Wenn eine Zahl q mit 0 < q < 1 existiert, so dass für alle (bis auf endlich viele) k ∈ N die Ungleichung k |ak | ≤ q gilt, so ist
P∞
a absolut konvergent.
k=0
p k
P
b) Ist k |ak | ≥ 1 für alle (bis auf endlich viele) k ∈ N so ist ∞
k=0 ak divergent.
√
n
Korollar 2.23. Für jedes k ∈ N gilt limn→∞ nk = 1.
P
Satz 2.24 (Quotientenkriterium). Es sei ∞
k=0 ak eine Reihe mit ak 6= 0 für alle k ∈ N.
a) Wenn eine Zahl q mit 0 < q < 1 existiert, so dass für alle (bis auf endlich viele) k ∈ N die Ungleichung
P∞
k=0 ak absolut konvergent.
P
|a
|
b) Ist |ak+1
≥ 1 für alle (bis auf endlich viele) k ∈ N so ist ∞
k=0 ak divergent.
k|
P∞
P
Definition 2.25 (Cauchy-Produkt). Das Cauchy-Produkt der Reihen ∞
n=0 bn ist definiert durch
n=0 an und
∞
X
cn
mit cn =
n=0
n
X
|ak+1 |
|ak |
≤ q gilt, so ist
ak bn−k = a0 bn + a1 bn−1 + · · · + an−1 b1 + an b0 .
k=0
Satz 2.26 (Konvergenz des Cauchy-Produktes). Sind die Reihen
P∞
P
produkt gegen den Wert c = ( ∞
n=0 bn ).
n=0 an ) · (
P∞
n=0
an und
Definition 2.27 (Exponentialfunktion). Die Funktion exp : R → R, x 7→
P∞
n=0
xk
k=0 k!
P∞
bn absolut konvergent, so konvergiert auch Ihr Cauchy-
heißt Exponentialfunktion.
Satz 2.28 (Eigenschaften der Exponentialfunktion). Die Exponentialfunktion hat die folgenden Eigenschaften.
a) Für alle x, y ∈ R gilt exp(x + y) = exp(x) exp(y). .
b) exp : R → R ist streng monoton steigend
c) Für alle x ∈ R gilt exp(x) > 0.
eq = limk→∞ (1 + kq )k
P
rk
Definition 2.30. Für r ∈ R \ Q definieren wir er := exp(r) = ∞
k=0 k!
Satz 2.29. Für q ∈ Q gilt eq = exp(q)
und
3. Reelle Funktionen
Definition 3.1 (Stetigkeit). Es sei M ⊂ R und f : M → R eine Funktion. f heißt stetig im Punkt x0 ∈ M wenn zu jedem > 0 ein δ > 0
existiert, so dass für jedes y ∈ M mit |x0 − y| < δ auch |f (x0 ) − f (y)| < gilt. f heißt stetig auf M falls f für jedes x ∈ M stetig ist.
Satz 3.2 (Folgenstetigkeit). Es sei M ⊂ R. Eine Funktion M → R ist genau dann stetig im Punkt a ∈ M wenn für alle Folgen (an )n∈N mit
an ∈ M und an → a auch f (an ) → f (a) gilt.
Satz 3.3. Es seien M ⊂ R, N ⊂ R und f : M → R und g : N → R stetige Funktionen.
a) Sei M = N . es gilt: (i) Sei α, β ∈ R. Die Funktion αf + βg : x 7→ αf (x) + βg(x) ist stetig. (ii) Die Funktion f g : x 7→ f (x)g(x) ist
(x)
stetig. (iii)Sei g(x) 6= 0 für alle x ∈ M . Die Funktion fg : x 7→ fg(x)
ist stetig. (iv) Die Funktion x 7→ max{f (x), g(x)} ist stetig.
b) Sei g(N ) ⊂ M . Die Funktion f ◦ g : N → R, x 7→ f (g(x)) ist stetig.
Definition 3.4 (Häufungspunkt). Es sei M ⊂ R. Ein Punkt a ∈ R heißt Häufungspunkt von M falls gilt: Für jedes > 0 ist ]a−, a+[∩M 6= ∅.
Definition 3.5. Es sei M ⊂ R, f : M → R und a ein Häufungspunkt von M . Gibt es ein c ∈ R ∪ {−∞, ∞}, so dass für alle Folgen (xn )n∈N
mit xn ∈ M \ {a} gilt, dass limn→∞ f (xn ) = c, so nennt man c den Grenzwert von f in a. Schreibweise: c = limx→a f (x)
Definition 3.6. Es sei M ⊂ R nach rechts (bzw. nach links) unbeschränkt, d.h. für jedes R > 0 gibt es ein x ∈ M mit x > R (bzw.
x > R). Weiter sei f : M → R. Gibt es ein c ∈ R ∪ {−∞, ∞}, so dass für alle Folgen (xn )n∈N mit xn → ∞ (bzw. xn → −∞) gilt,
dass limn→∞ f (xn ) = c (bzw. limn→∞ f (xn ) = c), so nennt man c den Grenzwert von f in ∞ (bzw. in −∞). Schreibweise: c =
limx→∞ f (x) bzw. c = limx→−∞ f (x)
Definition 3.7. Es sei M ⊂ R, f : M → R und a ein Häufungspunkt von M . Gibt es ein c ∈ R ∪ {−∞, ∞}, so dass für alle Folgen (xn )n∈N
mit xn ∈ M und xn > a (bzw. xn < a) gilt, dass limn→∞ f (xn ) = c, so nennt man c den rechtsseitigen Grenzwert von f in a (bzw.
den linksseitigen Grenzwert von f in a) . Schreibweise: c = limx→a,x>a f (x) bzw. c = limx→a,x<a f (x)
Satz 3.8. Es sei M ⊂ R, a ∈ M und f : M → R. Die folgenden Aussagen sind äquivalent:
(i) f ist stetig in a.
(ii) Der Grenzwert limx→a f (x) existiert und ist gleich f (a).
(iii) Der rechtseitige Grenzwert limx→a,x>a f (x) und der linksseitige Grenzwert limx→a,x<a f (x) existieren beide und beide sind gleich
f (a).
Definition 3.9. Es sei f : M → R eine Abbildung. f hat ein (globales) Maximum in x ∈ M falls f (y) ≤ f (x) für alle y ∈ M gilt. f hat
ein (globales) Minimum in x ∈ M falls f (y) ≥ f (x) für alle y ∈ M gilt.
Definition 3.10. Eine Teilmenge M ⊂ R heißt kompakt, wenn sie abgeschlossen und beschränkt ist.
Satz 3.11. Eine Menge M ⊂ R ist genau dann kompakt, wenn jede Folge (xn )n∈N mit xn ∈ M eine in M konvergente Teilfolge besitzt.
Satz 3.12. Es sei f : R → R eine stetige Funktion. Es gilt: a)Ist M ⊂ R kompakt, so ist f (M ) kompakt. b)Ist N ⊂ R offen so ist f −1 (N )
offen. c)Ist N ⊂ R abgeschlossen so ist f −1 (N ) abgeschlossen.
Satz 3.13 (Existenz von Maxima und Minima). Ist f : M → R eine stetige Funktion und ist M nichtleer und kompakt, so nimmt f ein
Maximum und ein Minimum auf M an.
Satz 3.14 (Nullstellensatz von Bolzano). Es sei I = [a, b] ein kompaktes Intervall und f : I → R eine stetige Funktion mit f (a)f (b) < 0.
Dann gibt es ein x ∈ I mit f (x) = 0.
Satz 3.15 (Zwischenwertsatz). Es sei I = [a, b] ein kompaktes Intervall und f : I → R eine stetige Funktion mit f (a) ≤ f (b). Für jedes
y ∈ [f (a), f (b)] gibt es ein x ∈ [a, b] mit f (x) = y.
Satz 3.16. Ist I ein (nicht notwendigerweise beschränktes) Intervall, M ⊂ R und f : I → M stetig. Es gilt a) f (I) ist ein Intervall. b) Ist f
injektiv, so ist f streng monoton steigend oder streng monoton fallend. c) Ist f bijektiv, so ist f −1 stetig.
Satz 3.17 (Logarithmus). a) Die Logarithmus Funktion ln : R+ → R, x 7→ exp−1 (x) ist stetig. b)Für alle x, y ∈ R+ gilt ln(xy) = ln(x) + ln(y).
c) ln(1) = 0 d) limx→0,x>0 ln(x) = −∞ und limx→∞ ln(x) = ∞.
Definition 3.18 (Die Ableitung). Es sei I eine offene Teilmenge von R. Eine Funktion f : I → R heißt differenzierbar in p ∈ I falls der
(p)
Grenzwert c = limx→p f (x)−f
existiert. In diesem Fall nennt man c die Ableitung von f in p. Gebräuchliche Notationen für die Ableitung
x−p df
df 0
sind: c = f (p) = dx (p) = dx x=p . Ist f für alle Punkte aus I differenzierbar so nennt man f differenzierbar und die Funktion f 0 : I → R,
x 7→ f 0 (x) die Ableitung von f .
Satz 3.19 (Rechenregeln für Ableitungen). Es sei I eine offene Teilmenge von R. Die Funktionen f : I → R und g : I → R seien in x ∈ I
differenzierbar.
a) f + g ist differenzierbar in x und es gilt (f + g)0 (x) = f 0 (x) + g 0 (x).
b) f · g ist differenzierbar in x und es gilt (f · g)0 (x) = f0 (x)g(x)
+ f (x)g 0 (x).
c) Ist g(x) 6= 0 so ist
f
g
differenzierbar in x und es gilt
f
g
0
(x) =
f 0 (x)g(x)−f (x)g 0 (x)
.
g(x)2
Satz 3.20 (Die Kettenregel). Es seien I und J offene Intervalle und f : I → J, g : J → R differenzierbare Funktionen. Dann ist g ◦ f : I → R
differenzierbar und für jedes x ∈ I gilt (g ◦ f )0 (x) = (g 0 ◦ f )(x)f 0 (x).
Satz 3.21 (Die Ableitung der Umkehrfunktion). Es sei I ein offenes Intervall. Die Funktion f : I → f (I) ⊂ R sei bijektiv und im Punkt
x ∈ I differenzierbar mit f 0 (x) 6= 0. Dann ist die Umkehrabbildung g = f −1 : f (I) → I im Punkt y = f (x) differenzierbar mit Ableitung:
1
g 0 (y) = f 0 (g(y))
= f 01(x) .
Definition 3.22 (Lokale Extrema). Es sei M ⊂ R und f : M → R.
a) f hat ein lokales Minimum in x0 ∈ M falls es ein > 0 gibt, so dass f (x0 ) ≤ f (x) für alle x ∈]x0 − , x0 + [∩M gilt.
b) f hat ein lokales Maximum in x0 ∈ M falls es ein > 0 gibt, so dass f (x0 ) ≥ f (x) für alle x ∈]x0 − , x0 + [∩M gilt.
Satz 3.23 (Permanentsprinzip). Ist f : M → R stetig, M offen und und p ∈ M mit f (p) 6= 0, so gibt es ein > 0, so dass f (x) 6= 0 für alle
x ∈]p − , p + [ gilt.
Satz 3.24 (Notwendiges Kriterium für Extrema). Es sei I ⊂ R ein offenes Intervall. Die Funktion f : I → R sei in x0 differenzierbar und
habe in x0 ein lokales Extrema. Dann gilt f 0 (x) = 0.
Satz 3.25 (Satz von Rolle). Es sei I = [a, b] ein kompaktes Intervall. Die Funktion f : I → R sei stetig, auf dem offenen Intervall ]a, b[
differenzierbar, und es sei f (a) = f (b). Dann gibt es einen Punkt x0 ∈]a, b[ mit f 0 (x0 ) = 0.
Satz 3.26 (Mittelwertsatz der Differentialrechnung). Es sei I = [a, b] ein kompaktes Intervall. Die Funktion f : I → R sei stetig, auf dem
offenen Intervall ]a, b[ differenzierbar.
(a)
a) Es gibt einen Punkt x0 ∈]a, b[ mit f 0 (x0 ) = f (b)−f
.
b−a
b) Sei g : I → R eine weitere stetige und auf ]a, b[ differenzierbare Funktion. Für alle x ∈]a, b[ gelte g 0 (x) 6= 0. Dann ist g(a) 6= g(b)
0
(x0 )
(b)−f (a)
= fg(b)−g(a)
.
und es gibt ein x0 ∈]a, b[ mit fg0 (x
0)
Satz 3.27 (Monotone Funktionen). Ist I ⊂ R ein offenes Intervall und f : M → R differenzierbar.
a) Ist f 0 (x) = 0 für alle x ∈ I dann ist f konstant.
b) f ist monoton steigend (monoton fallend) genau dann wenn f 0 (x) ≥ 0 (f 0 (x) ≤ 0) für alle x ∈ I.
c) Ist f 0 (x) ≥ 0 (f 0 (x) ≤ 0) für alle x ∈ I. Gibt es zu jedem x ∈ I mit f 0 (x) = 0 ein > 0 so dass f 0 (x) > 0 (f 0 (x) < 0) für alle
x ∈ [x − , x + ] \ {x} dann und nur dann ist ist f streng monoton steigend (streng monoton fallend). Insbesondere ist f streng
monoton steigend (fallend) falls f 0 (x) > 0 (f 0 (x) < 0) für alle x ∈ I.
Definition 3.28 (Mehrfache Differenzierbarkeit). Es sei I ⊂ R offen und f : I → R differnzierbar. f heißt stetig differenzierbar in x0 ∈ I,
wenn die Ableitung f 0 : I → R stetig in x0 ist. f heißt zweifach differenzierbar in x0 ∈ I, wenn die Ableitung f 0 differenzierbar in x0 ist.
f heißt n-fach differenzierbar in x0 ∈ I, wenn der Grenzwert f (n) (x0 ) := (f (n−1) )0 (x0 ) existiert. f heißt n-fach stetig differenzierbar
in x0 ∈ I, wenn die n-te Ableitung in x0 existiert und stetig ist.
Satz 3.29 (Hinreichendes Kriterium für lokale Extrema). Es sei I ⊂ R offen und f : I → R zweimal stetig differenzierbar. Weiter sei x0 ∈ I
mit f 0 (x0 ) = 0.
a) Ist f 00 (x0 ) > 0 so hat f ein lokales Minimum in x0 .
b) Ist f 00 (x0 ) < 0 so hat f ein lokales Maximum in x0 .
Satz 3.30 (Regel von l’Hospital). Es sei I ⊂ R offen und f, g : I → R differenzierbar.
a) Zu a ∈ I oder a Häufungspunkt von I gelte g(x) 6= 0 in einer Umgebung von a und limx→a f (x) = limx→a g(x) ∈ {0, −∞, ∞}. Falls
0
0
0
(x)
(x)
(x)
(x)
der Grenzwert limx→a fg0 (x)
existiert (Im Sinne von limx→a fg0 (x)
∈ R ∪ {−∞, ∞}) so gilt limx→a fg(x)
= limx→a fg0 (x)
.
b) Zu a = −∞ (oder a = ∞) gelte g(x) 6= 0 für alle x groß genug (klein genug). Weiter gelte limx→a f (x) = limx→a g(x) ∈ {0, −∞, ∞}.
0
0
0
(x)
(x)
(x)
(x)
Falls der Grenzwert limx→a fg0 (x)
existiert (Im Sinne von limx→a fg0 (x)
∈ R ∪ {−∞, ∞}) so gilt limx→a fg(x)
= limx→a fg0 (x)
.
Korollar 3.31. Ist p ein Polynom, so gilt limx→∞
p(x)
exp(x)
=0
und
limx→∞
exp(x)
p(x)
= ∞.
Definition 3.32 (Treppenfunktionen). Eine Funktion t : [a, b] → R heißt Treppenfunktion, falls es endlich viele Punkte x0 < x1 < · · · < xn
Rb
mit x0 = a und xn = b gibt, so dass f auf jedem der offenen Intervalle ]xk−1 , xk [, k = 1, . . . , n konstant ist. Den Wert a t(x) dx :=
Pn
xk−1 +xk
(xk − xk−1 ) nennt man Integral der Treppenfunktiuon t. Die Menge der Treppenfunktionen auf dem kompakten Intervall
k=1 t
2
[a, b] nennen wir T ([a, b]).
Definition
3.33 (Oberintegral und Unterintegral). Eso sei f : [a,nb] → R eine beschränkte Funktion. Weiter sei U(fo) =
nR
Rb
b
t(x)
dx
|
t ∈ T ([a, b]) mit t(x) ≤ f (x) für alle x ∈ [a, b] und O(f ) =
t(x) dx | t ∈ T ([a, b]) mit t(x) ≥ f (x) für alle x ∈ [a, b] Die
a
a
Zahl sup U(f ) heißt Unterintegral von f und die Zahl inf U heißt Oberintegral von f .
Definition 3.34 (Riemann-integrierbare Funktionen). Eine Funktion f : [a, b] → R heißt (Riemann)-integrierbar falls sie beschränkt ist
und sup U(f ) = inf O(f ) gilt.
Satz 3.35 (Eigenschaften integrierbare Funktionen). Es seien f : [a, b] → R und g : [a, b] → R auf dem Intervall I integrierbar. Dann gilt:
Rb
Rb
Rb
Rb
a) Die Funktionen f + g und λf (mit λ ∈ R) sind integrierbar und es gilt a (f + g)(x) dx = a f (x) dx + a g(x) dx und a λf (x) dx =
Rb
λ a f (x) dx.
Rb
Rb
b) Gilt f (x) ≤ g(x) für alle x ∈ I so ist a f (x) dx ≤ a g(x) dx.
−
−
c) Die Funktionen f + : I → R, f + (x) := max{f (x), 0} und
f R : I → R, f (x) := | min{f (x), 0}| sind integrierbar.
R b
b
d) Die Funktion |f | ist integrierbar und es gilt a f (x) dx ≤ a |f (x)|dx
e) Die Funktion f · g ist integrierbar.
Rγ
Rβ
Rγ
f) Es sei a ≤ α < β < γ ≤ b. Die eingeschränkte Funktion f |[α,γ] ist integrierbar. Es gilt α f (x) dx = α f (x) dx + β f (x) dx.
Satz 3.36 (Integrierbarkeit stetiger Funktionen). Ist f : K → R auf einem kompakten Intervall K stetig, so ist f auf K integrierbar.
R1√
Definition 3.37 (π). Die Zahl 4 0 1 − x2 dx nennet man Kreiszahl. Die Kreiszahl wird mit π bezeichnet.
Definition 3.38 (Stammfunktion). Es sei f :]a, b[→ R eine Funktion. Die Funktion F : [a, b] → R heißt Stammfunktion von f falls F
differenzierbar auf ]a, b[ ist und für alle x ∈]a, b[ die Gleichung F 0 (x) = f (x) gilt.
Rb
Satz 3.39 (Mittelwertsatz der Integralrechnung). Es sei f : [a, b] → R eine stetige Funktion. Es gibt ein ξ ∈ [a, b] mit a f (x) dx = f (ξ)·(b−a).
Satz 3.40 (Hauptsatz der Integralrechnung). Es sei f : [a, b] → R eine stetige Funktion.
Rx
a) f hat eine Stammfunktion. Diese ist von der Form F : [a, b] → R, x 7→ d f (t) dt + c mit d ∈ [a, b] und c ∈ R.
Rβ
b) Ist F eine Stammfunktion von f so gilt für alle α, β ∈ [a, b] α f (t) dt = F (β) − F (α).
Satz 3.41 (Partielle Integration). Es seien f : I → R und g : I → R stetig differenzierbare Funktionen auf einem Intervall I. Für beliebige
Rb
Rb
a, b ∈ I gilt a f (t)g 0 (t) dt = f (b)g(b) − f (a)g(a) − a f 0 (t)g(t) dt.
Rb
Satz 3.42 (Substitution). Es seien I und J reelle Intervalle, f : I → R stetig und g : J → I stetig differenzierbar. Dann gilt: a f (g(t))g 0 (t) dt =
R g(b)
f (x) dx. für alle a, b ∈ J.
g(a)
R b 0 (x)
Satz 3.43 (Logarithmisches Integrieren). Es sei g : I → R eine differenzierbare und nullstellenfreie Funktion auf [a, b]. Dann gilt: a gg(x)
dx =
log |g(b)| − log |(g(a))|.
Rx
Definition 3.44 (Uneigentliche Integrale). Es sei I ein Intervall (beschränkt oder unbeschränkt) und c ∈ I. Das Integral c f (t) dt existiere
Rx
für alle x ∈ I. Weiter sei α entweder ein Häufungspunkt von I oder α ∈ {−∞, ∞}. Existiert nun der Grenzwert limx→α c f (t) dt, so nennt
Rα
Rx
Rx
f (t) dt :=
man den Wert dieses Grenzwert Uneigentliches Integral von f über [c, α[. Schreibweise: c f (t) dt := limx→α c f (t) dt,
α
Rc
R∞
Rx
Rx
Rc
limx→α x f (t) dt bzw. c f (t) dt := limx→∞ c f (t) dt,
f
(t)
dt
:=
lim
f
(t)
dt.
x→−∞ x
−∞
Ry 1
Definition 3.45 (Die Arcustangens-Funktion). Die Funktion arctan : R → R, y 7→ 0 1+s
2 ds heißt Arcustangensfunktion.
Satz 3.46. Die Arcustangensfunktion ist injektiv und es gilt arctan(R) =] −
π̃ π̃
, [
2 2
mit π̃ := 4 arctan(1).
˜ :] −
Definition 3.47 (Tangens-Funktion). Es sei tan
R die Umkehrfunktion der Arcustangens-Funktion und R̃ := R \ { π̃2 + kπ̃}. Die
˜ auf R̃, d.h. für alle α ∈ R̃ gilt tan(α + π̃) = tan(α).
Tangens-Funktion tan : R̃ → R ist die π̃-periodische Fortsetzung von tan
π̃ π̃
, [→
2 2
Satz 3.48. Für alle α ∈ R \ { π̃2 + kπ̃} gilt tan0 (α) = 1 + (tan(α))2 .
˜ :] −
Definition 3.49 (Cosinus- und Sinus-Funktion). Es sei tan
π̃ π̃
, [→
2 2
R die Umkehrfunktion der Arcustangens-Funktion.
1
,
1+(tan(α))2
tan(α)
a) Die Cosinus-Funktion cos : R → R ist durch cos(α) = √
b) Die Sinus-Funktion sin : R → R ist durch sin(α) = √
Satz 3.50. Für alle α ∈ R gilt
a) cos(α) = cos(−α) und sin(α) = − sin(−α).
1+(tan(α))2
cos( π̃2 ) = 0 und cos(α + π̃) = − cos(α) definiert.
, sin( π̃2 ) = 1 und sin(α + π̃) = − sin(α) definiert.
b) cos(α + 2π̃) = cos(α) und sin(α + 2π̃) = sin(α).
c) (sin(α))2 + (cos(α))2 = 1.
d) sin0 (α) = cos(α) und cos0 (α) = − sin(α).
R1√
Satz 3.51. Es gilt: π̃ = π := 4 0 1 − x2 dx.
4. Funktionenfolgen
Definition 4.1 (Funktionenfolgen). Gegeben sei I ⊂ R und zu jedem n ∈ N eine Funktion fn : I → R. Die numerierte Menge der Funktionen
fn , n ∈ N heißt Funktionenfolge und wird mit (fn )n∈N bezeichnet.
Definition 4.2 (Punktweise Konvergenz). Die Funktionenfolge (fn )n∈N heißt Punktweise konvergent gegen eine Funktion f : I → R falls
die Folge (fn (x))n∈N für jedes x ∈ I gegen f (x) konvergiert.
Definition 4.3 (Gleichmäßige Konvergenz). Die Funktionenfolge (fn )n∈N heißt gleichmäßig konvergent gegen eine Funktion f : I → R
falls dn := supx∈I |fn (x) − f (x)| gegen Null konvergiert.
Satz 4.4. Ist fn : I → R für jedes n ∈ N stetig und konvergiert (fn )n∈N gleichmäßig gegen f : I → R, so ist f stetig.
Satz 4.5. Ist fn : [a, b] → R für jedes n ∈ N stetig und ist (fn )n∈N gleichmäßig konvergent gegen eine Funktion f : I → R, so gilt
Rb
Rb
limn→∞ a fn (x) dx = a f (x) dx.
Satz 4.6. Ist I ⊂ R offen und fn : I → R für jedes n ∈ N stetig differenzierbar. Ist die Funktionenfolge (fn )n∈N punktweise konvergent gegen
eine Funktion f : I → R und ist die Funktionfolge (fn0 )n∈N gleichmäßig konvergent gegen eine Funktion f˜ : I → R, so ist f differenzierbar und
(fn0 )n∈N konvergiert gegen f 0 .
Definition 4.7 (Potenzreihen). Es sei (an )n∈N eine Folge und x0 ∈ R. Durch (an )n∈N und x0 werde eine Funktionenfolge (fn )n∈N aus
P
P∞
Pn
k
k
k
Polynomen fn (x) = n
k=0 ak (x − x0 ) definiert. Den Grenzwert für n → ∞ , also
k=0 ak (x − x0 ) := limn→∞
k=0 ak (x − x0 ) , nennt
man Potenzreihe. Die Zahlen ak ∈ R nennt man Koeffizienten, die Zahl x0 den Entwicklungspunkt der Potenzreihe. Die Menge
I := {x ∈ R | (fn (x))n∈N ist konvergent} heißt Konvergenzbereich der Potenzreihe.
P
k
Satz 4.8. Es sei (ak )k∈N eine Folge und ∞
k=0 ak (x − x0 ) die dazugehörige Potenzreihe. Es gilt:
a) Es gibt einen Wert R ∈ {0} ∪ R ∪ {+∞} (den sogenannten Konvergenzradius) mit den Eigenschaften:
P
(i) Ist |x − x0 | < R so ist ∞
a (x − x0 )k konvergent.
Pk=0 k
k
(ii) Ist |x − x0 | > R so ist ∞
k=0 ak (x − x0 ) divergent.
|ak |
k|
k|
∈ R ∪ {∞} so ist R = limk→∞ |a|ak+1
.
b) Existiert der Grenzwert limk→∞ |ak+1 | uneigentlich (d.h. limk→∞ |a|ak+1
|
|
c) Es gilt
p

0
falls ( k |ak |)k∈N unbeschränkt


p
1
√
falls
lim supk→∞ k |ak | ∈ R+
R=
k |a |
lim
sup
k
k→∞

p

∞
falls
lim supk→∞ k |ak | = 0
p
p
Hierbei ist lim supk→∞ k |ak | der größte Häufungspunkt der Folge ( k |ak |)k∈N .
d) Auf jedem abgeschlossenen Intervall [a, b] ⊂]x0 − R, x0 + R[ konvergiert die Funktionenfolge (fn )n∈N , fn : [a, b] → R, fn (x) =
Pn
k
k=0 ak (x − x0 ) gleichmäßig.
P∞
P
k
Satz 4.9. Ist k=0 ak (x − x0 )k eine Potenzreihe mit Konvergenzradius R, so gilt für f :]x0 − R, x0 + R[→ R, x 7→ ∞
k=0 ak (x − x0 )
P∞
P
a) Die Potenzreihe k=0 kak (x − x0 )k−1 hat Konvergenzradius R und es gilt f 0 (x) = ∞
ka (x − x )k−1 .
P∞ ak
P∞ akk=0 k k+1 0
k+1
b) Die Potenzreihe k=0 k+1 (x − x0 )
hat Konvergenzradius R und F (x) = k=0 k+1 (x − x0 )
ist eine Stammfunktion von f .
Definition 4.10 (Taylorpolynom und Taylorreihe). Sei f : I → R eine n-mal differenzierbare Funktion, I offen und p ∈ I. Das Polynom
P
f (k) (p)
Tn (x) := n
(x − p)k heißt Taylorpolynom von f im Entwicklungspunkt p. Ist f beliebig oft differenzierbar, so nennt man die Reihe
k=0
k!
Pn f (k) (p)
k
(x − p) Taylorreihe von f im Punkt p.
k=0
k!
Satz 4.11. Sei f : I → R eine n-mal differenzierbare Funktion, M ⊂ I offen und p ∈ M . Das Taylorpolynom Tn ist das einizige Polynom
(k)
vom Grad n mit der Eigenschaft Tn (p) = f (k) (p), k = 1, . . . , n.
Satz 4.12 (Satz von Taylor). Sei f : I → R eine n + 1-mal differenzierbare Fuktion, I ein offens Intervall und p ∈ M . Zu jedem x ∈ I \ {p}
gibt es ein ξ zwischen x und p so dass f (x) = Tn (x) + Rn,x
mit
Rn,x =
f (n+1) (ξ)
(n+1)!
· (x − p)n+1 gilt.
Satz 4.13. Sei f : I → R eine beliebig oft differenzierbare Fuktion, I ein offenes Intervall und p ∈ I. Gibt es Zahlen M > 0 und C > 0 so
P
f (k) (p)
dass |f (n) (x)| ≤ M · C n für alle n ∈ N und alle x ∈ I gilt, so ist f (x) = ∞
(x − p)k für alle x ∈ I.
k=0
k!
Satz 4.14. Für alle x ∈ R gilt sin(x) =
P∞
k=0
(−1)k x2k+1
(2k+1)!
und cos(x) =
P∞
k=0
(−1)k x2k
.
(2k)!