Gewinnfunktion - Antonkriegergasse

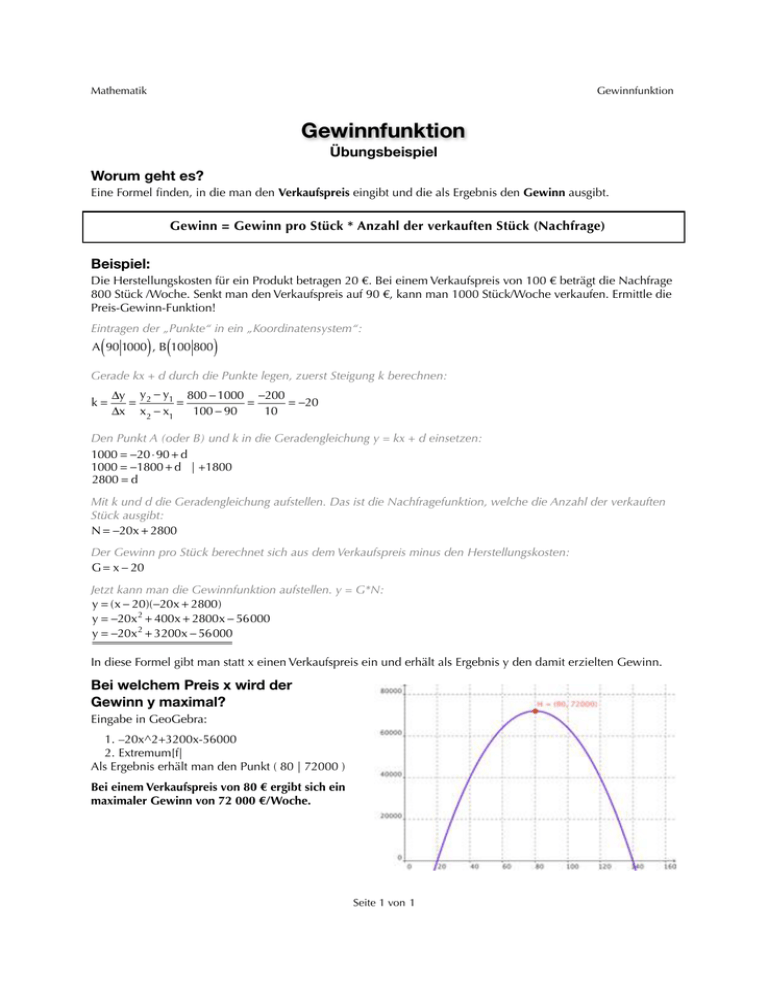
Mathematik
Gewinnfunktion
Gewinnfunktion
Übungsbeispiel
Worum geht es?
Eine Formel finden, in die man den Verkaufspreis eingibt und die als Ergebnis den Gewinn ausgibt.
Gewinn = Gewinn pro Stück * Anzahl der verkauften Stück (Nachfrage)
Beispiel:
Die Herstellungskosten für ein Produkt betragen 20 €. Bei einem Verkaufspreis von 100 € beträgt die Nachfrage
800 Stück /Woche. Senkt man den Verkaufspreis auf 90 €, kann man 1000 Stück/Woche verkaufen. Ermittle die
Preis-Gewinn-Funktion!
Eintragen der „Punkte“ in ein „Koordinatensystem“:
(
) (
A 90 1000 , B 100 800
)
Gerade kx + d durch die Punkte legen, zuerst Steigung k berechnen:
k=
Δy y 2 − y1 800 − 1000 −200
=
=
=
= −20
Δx x 2 − x1
100 − 90
10
Den Punkt A (oder B) und k in die Geradengleichung y = kx + d einsetzen:
1000 = −20 ⋅ 90 + d
1000 = −1800 + d | +1800
2800 = d
Mit k und d die Geradengleichung aufstellen. Das ist die Nachfragefunktion, welche die Anzahl der verkauften
Stück ausgibt:
N = −20x + 2800
Der Gewinn pro Stück berechnet sich aus dem Verkaufspreis minus den Herstellungskosten:
G = x − 20
Jetzt kann man die Gewinnfunktion aufstellen. y = G*N:
y = (x − 20)(−20x + 2800)
y = −20x 2 + 400x + 2800x − 56000
y = −20x 2 + 3200x − 56000
In diese Formel gibt man statt x einen Verkaufspreis ein und erhält als Ergebnis y den damit erzielten Gewinn.
Bei welchem Preis x wird der
Gewinn y maximal?
Eingabe in GeoGebra:
1. –20x^2+3200x-56000
2. Extremum[f|
Als Ergebnis erhält man den Punkt ( 80 | 72000 )
Bei einem Verkaufspreis von 80 € ergibt sich ein
maximaler Gewinn von 72 000 €/Woche.
Seite 1 von 1