Auf- und Entladekurven von Kondensatoren

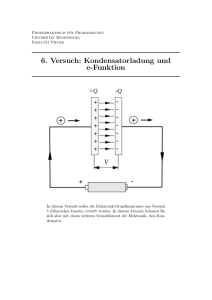
Physik-Labor
Versuchsprotokoll:
Auf- und Entladekurven von Kondensatoren
Inhalt
-
Einführung
Geräte, Arbeitsmaterialien
Schaltungsaufbau, Meßaufbau
Aufgabenstellung und Auswertung
Fehlerdiskussion
Zusammenfassung
Einleitung
Die Einfachste Bauform für einen Kondensator ist der Plattenkondensator. Er besteht aus zwei großen,
parallel zueinander leitfähigen Platten. Schließt man die beiden Platten eines Kondensators an eine
Spannungsquelle, beispielsweise eine Batterie, an, fließen so lange positive Ladungen auf die eine und
negative auf die andere Platte, bis die Potentialdifferenz zwischen den Platten gleich der angelegten
Spannung ist. Kondensatoren dienen zur kurzzeitigen Ladungsspeicherung und zur Gleichrichtung von
Wechselspannung.
Aufgabe ist es, durch Spannungsmessung die Auf- Entladekurven eines Kondensators für den Strom
und die Spannung aufzunehmen. Die Zeitkonstante soll theoretisch und graphisch ermittelt werden.
Die Konstante ist eine Größe zur Kennzeichnung der zeitlichen Änderung einer nach einer e-Funktion
steigenden oder fallenden Spannung bzw. eines Stromes.
Arbeitsmaterialien und Geräte
Für den Aufbau des Versuches werden folgende Dinge benötigt:
- hps-Elektronik-Koffer
- hps-Kondesatoren 2 Stk. (2200 F +/- 20%, 25 V)
- hps-Widerstand 10k +/- 5%, 2W
- hps-Kippschalter mit 2 Durchgängen zum Auf- und Entladen der Kondis
- Data-Logger HP 3421 A und Netzgerät HP 6632A
- Computer mit Programm zur Aufnahme/Auswertung der Spannungswerte (Auf- bzw.
Endladespannung)
- Diverse Verbindungskabel
Versuchsaufbau der Schaltung
Aufgaben
1. Aufnahme der Auf- und Entladekurve der Kondensatoren durch Spannungmessung
- Spannungsverlauf
- Stromverlauf
2. Graphische Darstellung von Spannungsverlauf U=f(t) auf lin-lin-Papier, und Stromverlauf I=f(t)
auf log-lin-Papier.
3. Ermittlung der Zeitkonstante a.) theoretisch
b.) graphisch
4. Fehlerberechnung
2
Formeln für die Berechnung
Kapazität des Kondensators
C
Q
U
1As
1W
1F
V As
*
A V
s
Einheit : C
C = Kapazität eines Kondensators in F (Farad)
Q = Ladungsmenge in As
U = Spannung in Volt
Theoretische Zeitkonstante
R *C
Einheit :
= Zeitkonstante in Sekunden
R = Widerstand in
C = in Kapazität in Farad
Auf- und Entladung eines Kondensators
Aufladung U t
Us * 1 e
1
R*C
Entladung U t
U0 *e
1
R*C
Ut = Spannung am Kondensator zur Zeit t in Volt
Us = angelegte Gleichspannung in Volt
U0 = Spannung am Kondensator zu Beginn der Entladung
Versuchsdurchführung
Aufgabe 1
Die Meßschaltung wird nach dem Schaltplan aufgebaut. Es werden zwei Kondensatoren von jeweils
2200 F +/- 20 % und 25V parallel zueinander geschaltet, so kann die doppelte Menge an elektrischer
Energie gespeichert werden. Die Kondensatoren werden an eine Spannungsquelle mit 7 V über einen
Widerstand von 10 K geladen, dieser Widerstand ist in Reihe zu den Kondis geschaltet.
Die Mess-Schaltung wird so aufgebaut, da? mit dem hps 9126-Schalter die Spannungsquelle vom
Stromkreis abgetrennt werden kann.(Siehe Schaltplan)
Parallel zu dem Widerstand bzw. der zwei Kondis werden Kabel zur Spannungsmessung an den DataLogger angeschlossen, der Widerstand an die Buchsen 02 und die Kondensatoren an 03. Die
Spannungsquelle ist ein Netzgerät (HP 6632A). Data-Logger und Netzgerät sind an einen PC
angeschlossen. Die Bedienung und Steuerung erfolgt über ein Programm, daß unter anderem die
Messwerte übertragen kann in Excel-Tabellen.
Die Messwerte werden über einen Zeitraum von ca.5 min Aufgenommen bzw. wenn keine
Messwertveränderung mehr sichtbar ist.
Die Messparameter müssen vor der Messung noch eingegeben werden, Data-Logger, Netgerät und PC
vollziehen nach dem Einschalten noch einen Selbsttest. Das Steuerprogramm wird geladen und die
Parameter eingegeben:
- Geräteparameter für den Data-Logger
GN1: dcv02: Widerstand 10K
GN2: dcv03: Kondensator
Geräteparameter für das Netzgerät
einzel: iset 0,2 A
Takt: vset
von 10 bis 10
Schrittweite 0
Takt in 10 s
3
Eine Zählschleife in Taktschritten von 10 ermöglicht eine Aufnahme von einem Messwert in 10 sec.
Vor Beginn der Messung muß der Kondensator entladen werden, indem für kurze Zeit der Schalter im
Stromkreis so gelegt wird, daß die Stromquelle abgehängt ist oder einfach durch kurzschließen der
Positiven und Negativen Pole am Kondensator.
Der Schalter wird anschließend gleichzeitig mit Start der Messschleife umgelegt und die
Kondensatoren laden sich auf. Verändert sich die Spannung an den Kondensatoren nicht mehr, wird
die Stromquelle durch umlegen des Schalters abgeschaltet und der Kondensator entlädt sich wieder.
Der Strom läßt sich über die gemessene Spannung am Widerstand berechnen (I = U/R). Die
Sromstärke am Widerstand ist genauso hoch wie an dem Kondensatoren, da der Widerstand in Reihe
geschaltet ist. Zur Berechnung muß aber die Spannung am Widerstand genommen werden, da die
Kondis mit zunehmender Spannung auch größere Widerstände werden.
Meßtabelle
Aufladekurve des Kondesators
R/Kohm
t (sec)
U(R) in V
dcv02
10
10
6,6589
20
5,8378
30
4,6989
40
3,7958
50
3,1135
60
2,4919
70
2,0275
80
1,6533
90
1,3516
100
1,1089
110
0,9021
120
0,7516
130
0,6215
140
0,5167
150
0,4307
160
0,3619
170
0,3057
180
0,2595
190
0,2220
200
0,1912
210
0,1660
220
0,1458
230
0,1283
240
0,1140
250
0,1018
260
0,0926
U(K) in V
dcv03
0,4900
1,2837
2,3909
3,2171
3,8897
4,5350
4,9864
5,3500
5,6430
5,8798
6,0837
6,2267
6,3551
6,4553
6,5386
6,6056
6,6609
6,7063
6,7430
6,7731
6,7977
6,8180
6,8355
6,8485
6,8605
6,8692
Entladekurve des Kondensators
I (ges) in mA t (sec)
U(R) in V
U(K) in V
dcv02
dcv03
0,6659
10
-6,2048
6,1182
0,5838
20
-4,9932
4,9248
0,4699
30
-4,0291
3,9609
0,3796
40
-3,2555
3,2114
0,3114
50
-2,6011
2,5202
0,2492
60
-2,1378
2,1091
0,2027
70
-1,7357
1,7128
0,1653
80
-1,4110
1,3917
0,1352
90
-1,1489
1,1340
0,1109
100
-0,9368
0,9100
0,0902
110
-0,7650
0,7552
0,0752
120
-0,6259
0,6176
0,0622
130
-0,5130
0,5065
0,0517
140
-0,4213
0,4160
0,0431
150
-0,3467
0,3425
0,0362
160
-0,2861
0,2825
0,0306
170
-0,2339
0,2311
0,0260
180
-0,1964
0,1940
0,0222
190
-0,1634
0,1615
0,0191
200
-0,1365
0,1349
0,0166
210
-0,1145
0,1132
0,0146
220
-0,0964
0,0953
0,0128
230
-0,0815
0,0807
0,0114
240
-0,0693
0,0685
0,0102
250
-0,0592
0,0586
0,0093
I (ges) in mA
0,6205
0,4993
0,4029
0,3256
0,2601
0,2138
0,1736
0,1411
0,1149
0,0937
0,0765
0,0626
0,0513
0,0421
0,0347
0,0286
0,0234
0,0196
0,0163
0,0137
0,0114
0,0096
0,0082
0,0069
0,0059
Die negativen Spannungswerte für die Kondensatorentladung kommen deshalb zustande, da der Strom
bei umschalten des Schalters auf Entladung in die entgegengesetzte Richtung fließt.
4
Aufgabe 2a
Graphische Darstellung von Spannung als Funktion der Zeit
Spannungsverlauf Kondensatoraufladung
7,0000
6,0000
Spannung in Volt
5,0000
4,0000
3,0000
2,0000
1,0000
0,0000
0
50
100
150
Zeit (t) in sec
200
250
Spannungsverlauf
Kondensatoraufladung
Das Diagramm zeigt, daß sofort Spannung auf den Kondensator geladen wird. Der Strom ist nicht
konstant , sondern eine Funktion der Zeit.
5
Aufgabe 2b
Graphische Darstellung von I = f(t) auf log-lin-Papier
Aufladezeit Stromstärke
Log-Einheit
25
23
21
19
17
15
13
11
9
7
5
3
1
1,0000
0,1000
0,0100
0,0010
Meßpunkte Intervall 10 sec
Aufladezeit
Stromstärke
Aufgetragen wurden die Aufladestromstärke (berechnet aus I=U/R) gegen die Zeit. Es handelt sich um
eine logarithmische Abnahme des Stromes. Zum Vergleich das lin-lin-Diagramm.
Aufladestrom als Funktion der Zeit
0,7000
Strom in mA
0,6000
0,5000
0,4000
Aufladestrom in Funktion der Zeit
0,3000
0,2000
0,1000
0,0000
0
50
100
150
200
250
300
Zeit (t) in sec
Aufladestrom als Funktion der Zeit , der Startwert beträgt U/R und fällt exponentiell mit der Zeit ab.
6
Aufgabe 3
Theoretische Ermittlung der Zeitkonstante
Die Zeitkonstante ist eine Größe zur Kennzeichnung der Zeitlichen Änderung einer nach einer eFunktion steigenden oder fallenden Spannung bzw. Stromes. Die Zeitkonstante läßt sich berechnen
aus dem Produkt Widerstand und Kapazität. Für die Berechnung wird der Widerstand (R) und die
R *C
gesamte Ladungskapazität der Kondensatoren benötigt.
= Zeitkonstante
R = Widerstand 10 k
C = Ladung 4400 F
10000 * 0.0044 F
44 sec
Für die theoretische Zeitkonstante ergibt sich ein Wert von 44 sec.
Graphische Ermittlung der Zeitkonstante
Als Diagramm wurde die Spannung gegen die Zeit in der Aufladezeit des Kondensators aufgetragen
Spannung in Volt
Aufladespannung als Funktion der Zeit
7,0000
6,5000
6,0000
5,5000
5,0000
4,5000
4,0000
3,5000
3,0000
2,5000
2,0000
1,5000
1,0000
0,5000
0,0000
0
20
40
60
80
100 120 140 160 180 200 220 240 260
Aufladespanung als
Zeit (t) sec
Funktion der Zeit
Wenn der Kondensator 63 % des Endwertes der Aufladung von 7 Volt erreicht hat, gilt t = = R*C .
Bei konstantem Ladestrom wäre der Kondensator zu diesem Zeitpunkt schon voll aufgeladen.
Das bedeutet und ergibt für die graphische Zeitkonstante (7V 0.63 = 4,41 V)
einen Wert von
sec.
7
Fehlerrechnung
Durch die hohe Toleranz der einzelnen Bauteile ist eine Fehlerrechnung angebracht.
= 44 sec
R = 10000 +-5%
C= 4400 F +- 20%
R *C
Für den relativer Fehler von
R
R
44
addieren sich die Gesamtfehler der einzelnen Bauteile:
C
C
500
10000
880
4400
11
Die Zeitkonstante ist also fehlerbehaftet, es ergibt sich für die Zeitkonstante folgender Wert
44 (1+-0.25) sec. Das bedeute das auf Grund der hohen Toleranzen der Bauteile die Zeitkonstante
starken Schwankungen unterliegt, um genauere Ergebnisse zu Erreichen und Fehler einzugrenzen sind
Doppel- oder Dreifachbestimmungen von Vorteil.
Zusammenfassung
Diese Schaltung wird als RC-Kreis bezeichnet. Meist sind in solche Schaltungen die Ströme nicht
konstant, sondern eine Funktion der Zeit. Anwendung finden solche RC-Kreise in
Elektronenblitzgeräte in Photokameras. Vor jeder Aufnahme wird ein Kondensator aufgeladen, wobei
der Ladestrom von einer Batterie kommt, die mit dem Kondensator über einen Widerstand verbunden
ist. Im Moment des Auslösens entlädt sich der Kondensator durch die Blitzröhre.
Die Entladung erfolgt aber nicht linear sondern proportional zur vorhandenen Ladung. Diese Art des
Abfallens heißt exponentielle Abnahme. Sie ist typisch für viele Phämomene in der Natur.
Die theoretische Zeitkonstante ( ) beträgt 44 (1+-0.25) sec, die ermittelte
graphische Zeitkonstante ( ) 58 sec.
Anlage
Aufgabenblatt
PC-Ausdruck der Meßwerte
8