Der Betrag einer reellen Zahl

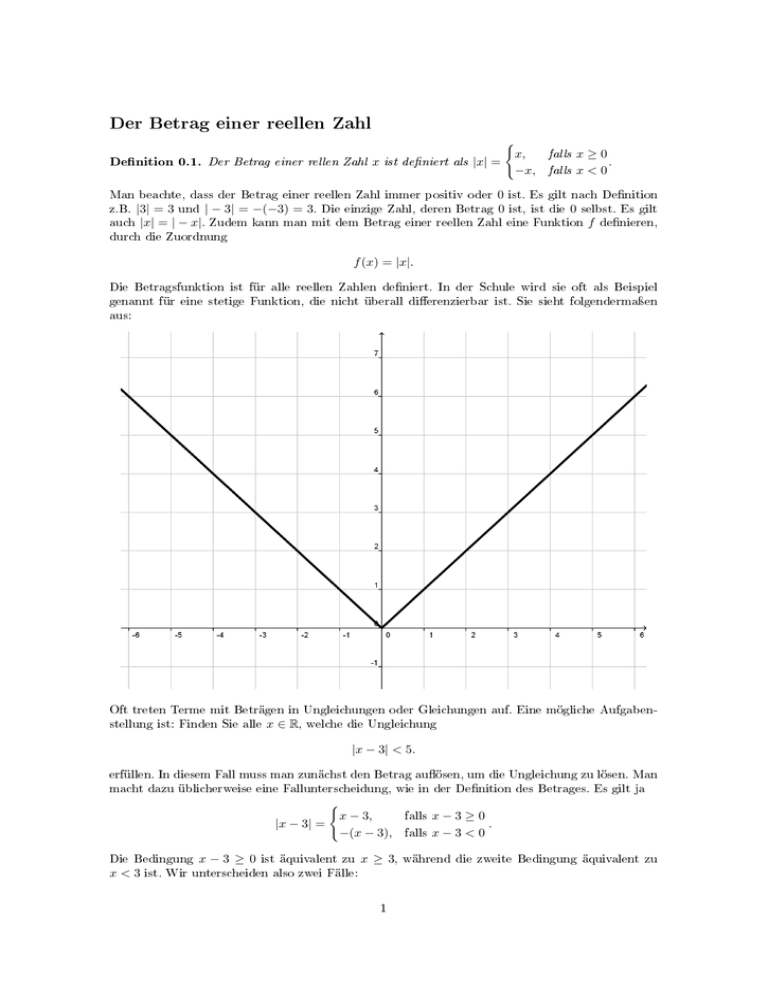
Der Betrag einer reellen Zahl
Denition 0.1.
(
x,
Der Betrag einer rellen Zahl x ist deniert als |x| =
−x,
falls x ≥ 0
.
falls x < 0
Man beachte, dass der Betrag einer reellen Zahl immer positiv oder 0 ist. Es gilt nach Denition
z.B. |3| = 3 und | − 3| = −(−3) = 3. Die einzige Zahl, deren Betrag 0 ist, ist die 0 selbst. Es gilt
auch |x| = | − x|. Zudem kann man mit dem Betrag einer reellen Zahl eine Funktion f denieren,
durch die Zuordnung
f (x) = |x|.
Die Betragsfunktion ist für alle reellen Zahlen deniert. In der Schule wird sie oft als Beispiel
genannt für eine stetige Funktion, die nicht überall dierenzierbar ist. Sie sieht folgendermaÿen
aus:
Oft treten Terme mit Beträgen in Ungleichungen oder Gleichungen auf. Eine mögliche Aufgabenstellung ist: Finden Sie alle x ∈ R, welche die Ungleichung
|x − 3| < 5.
erfüllen. In diesem Fall muss man zunächst den Betrag auösen, um die Ungleichung zu lösen. Man
macht dazu üblicherweise eine Fallunterscheidung, wie in der Denition des Betrages. Es gilt ja
(
x − 3,
falls x − 3 ≥ 0
|x − 3| =
.
−(x − 3), falls x − 3 < 0
Die Bedingung x − 3 ≥ 0 ist äquivalent zu x ≥ 3, während die zweite Bedingung äquivalent zu
x < 3 ist. Wir unterscheiden also zwei Fälle:
1
Fall 1:
x ≥ 3 In diesem Fall gilt wie oben gesehen |x − 3| = x − 3 und somit können wir die
Ungleichung nun lösen:
|x − 3| < 5 ⇔ x − 3 < 5 ⇔ x < 8
Die Ungleichung ist also für alle x ∈ R mit 3 ≤ x < 8 erfüllt (denn x ≥ 3 war ja unsere Bedingung
für diesen Fall!). Die Menge dieser x schreibt man üblicherweise als Intervall: [3, 8) oder [3, 8[.
Fall 2: x < 3 In diesem Fall gilt |x − 3| = −(x − 3) = −x + 3. Wir formen wieder wie oben um:
|x − 3| < 5 ⇔ −x + 3 < 5 ⇔ −2 < x.
Die Ungleichung ist folglich für alle x ∈ R mit −2 < x < 3 erfüllt. Auch diese Menge können wir
als Intervall (−2, 3) oder ] − 2, 3[ schreiben.
Um nun die gesamte Lösungsmenge zu erhalten, müssen wir die Mengen aus Fall 1 und Fall 2
zusammennehmen. In unserem Fall ist das genau das Intervall (−2, 8) oder ] − 2, 8[. Wir haben die
Ungleichung gelöst.
Bemerkung 0.2. Um Betragsgleichungen oder -ungleichungen zu lösen, sollte man in der Regel
Fallunterscheidungen verwenden. Das Quadrieren einer solchen Gleichung oder Ungleichung kann
zu falschen Lösungen führen. Als Beispiel betrachte man
|x| = −1.
Diese Betragsgleichung hat keine reelle Lösung, da für alle x ∈ R wie bereits erwähnt |x| ≥ 0 gilt.
Quadriert man diese Gleichung jedoch, so erhält man
x2 = 1,
und diese Gleichung hat die Lösungen x = 1 und x = −1.
2