Mehrdimensionale Zufallszahlen Mehrdimensionale Zufallszahlen (2)
Werbung
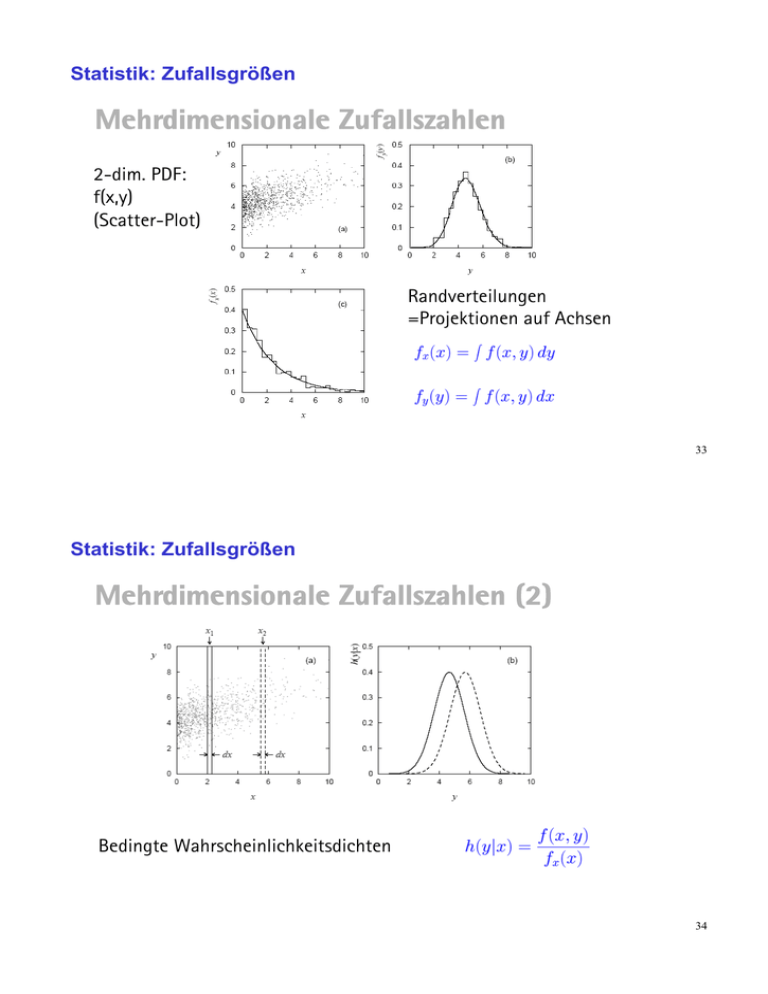
Statistik: Zufallsgrößen Mehrdimensionale Zufallszahlen 2-dim. PDF: f(x,y) (Scatter-Plot) Randverteilungen =Projektionen auf Achsen 33 Statistik: Zufallsgrößen Mehrdimensionale Zufallszahlen (2) Bedingte Wahrscheinlichkeitsdichten 34 Statistik: Verteilungen Binomialverteilung (1) 35 Statistik: Verteilungen Binomialverteilung (2) 36 Statistik: Verteilungen Poissonverteilung 37 Statistik: Verteilungen Poissonverteilung Anwendung: Bininhalt in einem Histogramm 38 Statistik: Verteilungen Normalverteilung 39 Statistik: Verteilungen Normalverteilung 40 Statistik: Verteilungen Standardverteilungen 41 Statistik: Zentraler Grenzwertsatz Zentraler Grenzwertsatz 42 Statistik: weitere Verteilungen Chi-Quadrat-Verteilung Beschreibt die Summe der quadratischen Abweichungen vom Erwartungswert einer n-dimensionalen Normalverteilung. (=Quadrat der Radien von n-dimensionalen Vektoren. In hochdimensionalen Räumen steckt das Volumen einer Kugel fast vollständig nahe der ,,Oberfläche´´.) 43 Statistik: weitere Verteilungen Cauchy- (=Breit-Wigner-) Verteilung Tritt bei allen Resonanzphänomenen auf, ist Fouriertransformierte (im Frequenz-=Energieraum) der Exponentialverteilung (in Zeit t). Unschärferelation: Resonanzbreite = h/Lebensdauer 44 Kovarianzmatrix Erwartungswert von (Abweichung vom Erwartungswert in Variable x) * (Abweichung vom Erwartungswert in Variable y): Diagonalwerte: Varianzen: Erwartungswert von (Abweichung vom Erwartungswert in Variable x)**2 1 Korrelationsmatrix Normiere Kovarianzmatrix, so dass die Diagonalelemente alle 1 sind: 2 Korrelation Wenn x, y unabhängig, d.h. dann gilt x und y ,,unkorreliert“ Achtung: Die umgekehrte Aussage gilt nicht immer 3 Variablentransformation I Eine Funktion a(x) einer ZufallsVariablen x mit pdf f(x) ist wieder eine Zufallsvariable, mit pdf g(a) Intervall im x-Raum, für das a in [a,a+da] Wahrscheinlichkeitsdichte für a 4 Variablentransformation II Wenn Inverse nicht eindeutig, müssen alle Zweige berücksichtigt werden. Beispiel: 5 Fehlerfortpflanzung I 6 Fehlerfortpflanzung II 7 Fehlerfortpflanzung III 8 Fehlerfortpflanzung IV 9 Fehlerfortpflanzung V 10 PseudoQuasiZufallszahlen Zufallszahlen regelmäßiges Gitter Monte Carlo 11 Paarbildung Bremsstrahlung 12 Parameterschätzung Parameterschätzung -- Fitting Maximum Likelihood Kleinste Quadrate Messung 13 Parameterschätzung mit kleinsten Quadraten 14 Lineare kleinste Quadrate Lineares Gleichungssystem eindeutig lösbar Überbestimmtes Gleichungssystem Ausgleichsrechnung, n-p Freiheitsgrade 15 Parameterschätzung mit kleinsten Quadraten 16 Lösung des linearen Optimierungsproblems 17 Abhängigkeit von der Messfehler-Verteilung Geradenfit an 20 Datenpunkte (ndf=20-2=18) Drei verschiedene Verteilungsfunktionen der Einzelmessungen, alle Mittelwert 0, Standardabweichung=0.5 18 Parameterschätzung mit kleinsten Quadraten 25000 Monte-Carlo-Tests: Alle Parameter-Verteilungen sind Gaussisch, die Breite kompatibel zur Erwartung aus Fehlerfortpflanzung (für beide Parameter) 19 Parameterschätzung mit kleinsten Quadraten 20 Robuste kleinste Quadrate Ausreisser in den Daten (z.B. Eingabefehler, falsche Messpunkte auf Spur) können Fit wegen quadratischer Abhängigkeit sehr stark beeinflussen und zu völlig sinnlosen Lösungen führen. Rezept zur Robustifizierung: 1. Normaler Kleinste Quadrate-Fit, liefert Residuen. 2. Modifiziere Daten durch Limitieren der Residuen auf c!. Eine gute Wahl ist c=1.5. 3. Wiederhole Fit mit Pseudo-Messungen statt Originalmessungen. Es existieren auch andere Loss-Funktionen (z.B. Huber-Funktion), aber nicht mehr analytisch lösbar. 21 2 Häufige Fehler bei " - Minimierung 22 2 Häufige Fehler bei " – Minimierung (Forts.) 23 2 Vorsicht bei kleinen Zahlen! Demo Soll-Resultat 24 2 Vorsicht bei kleinen Zahlen! 25 Nichtlineare kleinste Quadrate 26 Kleinste Quadrate mit Nebenbedingungen 27 Kleinste Quadrate mit Nebenbedingungen (2) 28