lin_fkt_einstieg_folien_loesungen

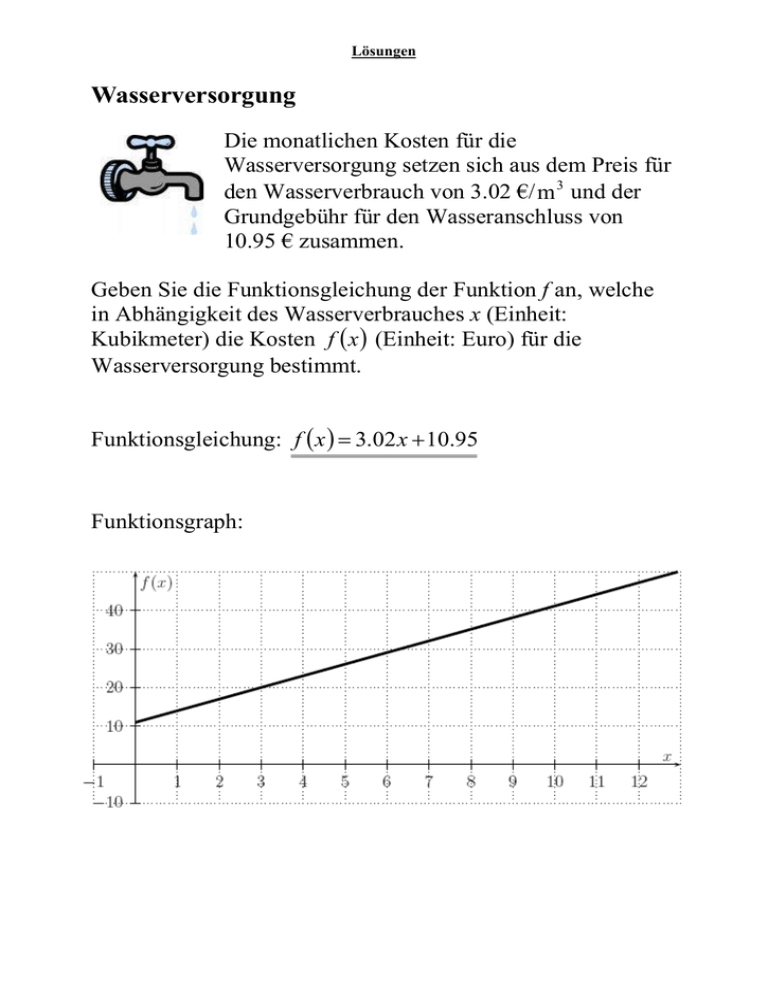
Lösungen
Wasserversorgung
Die monatlichen Kosten für die
Wasserversorgung setzen sich aus dem Preis für
den Wasserverbrauch von 3.02 €/ m 3 und der
Grundgebühr für den Wasseranschluss von
10.95 € zusammen.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit des Wasserverbrauches x (Einheit:
Kubikmeter) die Kosten f  x  (Einheit: Euro) für die
Wasserversorgung bestimmt.
Funktionsgleichung: f  x   3.02 x  10.95
Funktionsgraph:
Lösungen
Fallschirmspringer
Ein Fallschirmspringer öffnet in 255 Meter
über dem Erdboden seinen Fallschirm. Mit
konstanter Geschwindigkeit verliert er 4.5
Meter pro Sekunde an Höhe.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit der Zeit x (Einheit: Sekunden) die Höhe f x 
(Einheit: Meter) über dem Erdboden bestimmt.
Funktionsgleichung: f  x   4.5 x  255
Funktionsgraph:
Lösungen
Unterschriftensammlerin
Der Verdienst einer Unterschriftensammlerin
setzt sich an einem Arbeitshalbtag aus einem
fixen Grundbetrag von CHF 14.- und einer
Erfolgsprämie von CHF 1.80 pro Unterschrift
zusammen.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit der Anzahl Unterschriften x den Verdienst
f  x  (Einheit: CHF) an einem Arbeitshalbtag bestimmt.
Funktionsgleichung: f  x   1.8 x  14
Funktionsgraph:
Lösungen
Sängerin
Der Verdienst einer Sängerin setzt sich bei
einem Konzert aus einem fixen Grundbetrag
von CHF 7000.- und einer Erfolgsprämie von
CHF 1.60 pro BesucherIn zusammen.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit der Anzahl BesucherInnen x den Verdienst
f  x  (Einheit: CHF) der Sängerin bestimmt.
Funktionsgleichung: f  x   1.6 x  7000
Funktionsgraph:
Lösungen
Gasversorgung
Die monatlichen Kosten für die Gasversorgung
setzen sich aus dem Preis für den Gasverbrauch von
0.37 €/ m 3 und der Grundgebühr für den
Gasanschluss von 10.38 € zusammen.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit des Gasverbrauches x (Einheit: Kubikmeter)
die Kosten f  x  (Einheit: Euro) für die Gasversorgung
bestimmt.
Funktionsgleichung: f  x   0.37 x  10.38
Funktionsgraph:
Lösungen
Felgenbremsen
Bei einem Velo mit Felgenbremsen wird der
Abrieb der Bremsbacken gemessen: Zu Beginn
haben die Bremsbacken eine Dicke von 5.5
mm. Druchschnittlich nimmt die Dicke um
0.005 mm pro gefahrenen Kilometer ab.
Geben Sie die Funktionsgleichung der Funktion f an, welche
in Abhängigkeit der gefahrenen Strecke x (Einheit: Kilometer)
die Dicke f  x  (Einheit: Millimeter) der Bremsbacken
bestimmt.
Funktionsgleichung: f  x   0.005 x  5.5
Funktionsgraph:
Lösungen
Zusammenstellung aller Funktionsgleichungen
Wasserversorgung:
f  x   3.02 x  10.95
Fallschirmspringer:
f  x   4.5 x  255
Unterschriftensammlerin: f  x   1.8 x  14
Sängerin:
f  x   1.6 x  7000
Gasversorgung:
f  x   0.37 x  10.38
Felgenbremsen:
f  x   0.005 x  5.5