Gleichstrom-Formelmatura - e

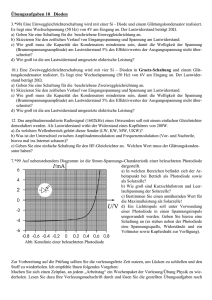
Berufsgrundbildung Elektrotechnik
Mathematische Grundlagen
"Gleichstrom - Formelmatura"
Die Berechnung eines belasteten Spannungsteilers (vgl. Grundlagen der
Elektrotechnik) stellt sozusagen eine "Gleichstromrechnung" für Fortgeschrittene dar.
Wir sind ihr deshalb bisher ausgewichen, weil man zum echten Verständnis dieser
Schaltung, die Strom- und Spannungsverhältnisse zuerst messtechnisch an konkreten Widerständen erfassen sollte. Für Spannungsteiler besteht vor allem in elektronischen Schaltungen, etwa zur Ansteuerung von Transistoren, ein riesiges Einsatzgebiet.
In fachrechnerischer Hinsicht bieten sich uns diesbezüglich aber Formeln der
"gehobenen Kategorie". Mit der erfolgreichen Umstellung einer einschlägigen Formel,
könnten wir durchaus davon sprechen, dass du die "Reifeprüfung" für Äquivalenzumformungen bestanden hast.
I
UE
I
R1, R2
RL
R1
UE
R2
RLast
UE
=
=
=
=
Eingangsspannung
Eingangsstrom
Widerstände des Spannungsteilers
Lastwiderstand
Diese Schaltung wird dich an die Reihengruppenschaltung
erinnern.


R .R 
I .  R1  2 L 
R2  RL 

Die "Maturaaufgabe" besteht nun in der Äquivalenzumformung dieser Gleichung
nach RL.

R2 . RL 

Unter Berücksichtigung des Ohmschen Gesetzes (U = I . R) handelt es sich bei  R1 

R

R
2
L 

offensichtlich um den Gesamtwiderstand dieses belasteten Spannungsteilers.
Umformung:
UE
I
 R1 
R 2 . RL
R 2  RL
UE
 R1
I
 UE

 R 1  .  R 2  R L  

 I

U

R 2 .  E  R 1   R L
 I

R 2 . RL
U

.  E  R 1 
 I

U

R L .  E  R 1   R 2 . R L
 I



R 2 . RL
U

 R 2 .  E  R 1 
 I

A-27

R 2 . RL
R 2  RL
 U


R L .  E  R 1   R 2 

 I

U

 R 2 .  E  R 1 
 I

U

 R 2 .  E  R 1 
 I

UE
 R1  R 2
I

RL

RL

R1 .R 2 
UE
.R 2
I
UE
 R1  R 2
I
In einer elektronischen Schaltung wird bei einer Eingangsspannung von 15V eine
Ausgangsspannung (Spannung am Lastwiderstand) von 3V benötigt. Die Eingangsstromstärke (I) beträgt 18mA. Die Widerstände des Spannungsteilers sind mit 667 
für R1 und 188  für R2 gegeben. Welchen Wert besitzt der Lastwiderstand, wenn
durch ihn ein Strom von 2mA fließt?
RL
UL
IL

RL

3
2 .103
RL
 1500 
Zur Überprüfung der Gleichungsumformung kennen wir damit den zu erhaltenden
Wert.
RL
RL

R1 .R 2 
UE
.R 2
I
UE
 R1  R 2
I
667 .188 
RL

15
.188
18 .103
15
 667  188
18 . 10 3
 1443 
Die Differenz zum Wert von 1500  ergibt sich durch eine Rechenungenauigkeit mit den gerundeten
Widerstandswerten von R1 (666,6 ) und R2 (187,5 ).
A-28