Station 1 - Spalatin Gymnasium

(Damit die Schriftart „Forte“ richtig dargestellt werden kann, musst Du diese Datei unter C:\Windows\fonts speichern.)
Station 1: Teilbarkeitsregeln
1. Beende folgende Sätze:
a)
b)
c)
d)
Eine Zahl ist durch 9 teilbar, wenn ...
Eine Zahl ist durch 4 teilbar, wenn ...
Eine Zahl ist durch 2 teilbar, wenn ...
Eine Zahl ist durch 6 teilbar, wenn ...
Level 1
einfach
2. Übertrage folgende Tabelle (auf die 2. Spalte darfst Du verzichten)
und setze überall dort ein Kreuz, wo Du eine Teilbarkeit erkennst.
2
3
4
5
6
9
10
100
a) 7 500
b) 2 345
c) 2 224
d) 31 860
3. Gib eine fünfstellige Zahl an, die in der Tabelle aus Aufgabe 2
folgende Eintragungen liefern würde!
?????
X
X
X
4. Überprüfe die Teilbarkeit mit Hilfe der Summenregel
und gib die Begründung so an, wie Du es gelernt hast.
7 | 235, denn ...
8 | 3 340, denn ...
12 | 3510, denn ...
5. Formuliere eine Regel für die Teilbarkeit durch 200 !
Level 2
Standard
Level 3
knifflig
6. Nenne eine Zahl, die durch 2, 3, 9 und 11 teilbar ist.
7. Begründe ohne zu rechnen, dass 1 465 832 nicht durch 21
teilbar ist.
Level 4
Knobeln
Station 2: gemeinsame Teiler und Vielfache
1. Bestimme die folgenden Vielfachen-Mengen. Denke daran,
immer mindestens 4 Elemente auszuschreiben!
V6 = {...}
V45 = {...}
V33 = {...}
Level 1
einfach
1. In den folgenden Aufgaben sind 3 falsche Zahlen enthalten.
Zudem fehlen 3 Teiler. Finde die Fehler!
a) T18 = {1, 2, 3, 6, 9, 18}
g) T48 = {1, 2, 3, 6, 8, 12, 16, 24, 48}
b) T27 = {1, 3, 9, 27}
h) T50 = {1, 2, 5, 10, 25, 50}
c) T31 = {1, 31}
i)
d) T32 = {1, 2, 4, 8, 12, 16, 32}
j) T64 = {1, 2, 3, 4, 16, 32, 64}
e) T49 = {1, 49}
k) T68 = {1, 2, 4, 17, 34, 68}
f) T45 = {1, 3, 5, 9, 15, 45}
l)
T61 = {1, 61}
T99 = {1, 3, 9, 11, 33, 66, 99}
3. Bestimme die gemeinsamen Teiler der folgenden Zahlenpaare. Gib auch jeweils den ggT an!
a) 48 und 18
b) 30 und 45
c) 84 und 60
Level 2
Standard
2. Gib die (ersten vier) gemeinsamen Vielfachen an!
V6∩V33 = {...}
V8∩V12 = {...}
V25∩V60 = {...}
4. Ergänze folgende Teilermengen:
a) T.... = {1, 5,
c)
.... }
b) T.... = {...., 3, 7, .... }
V7∩V11 = {...}
Level 3
knifflig
T.... = {1,2, ...., ...., ...., 8, 9, ...., ...., ...., 36, .... }
4. Um welche Vielfachmengen handelt es sich, wenn
a) ... 65 an fünfter Stelle steht? b) ... 112 an siebenter Stelle steht?
6. Wie könnten die Zahlen a und b lauten?
a) Va ∩Vb = {24, 48, 72, 96, ...}
b) Va ∩Vb = {
..... , ....., ....., ....., .....,
84, ... }
c) Va ∩Vb = {23, 46, 69, 92, ...}
Level 4
Knobeln
Station 3: Sachaufgaben zu kgV und ggT
1.
Eva und Andy schmücken ihre Wohnung weihnachtlich. Beim
Öffnen der Schachteln stellt Eva fest, dass von ihrer Schafherde nur noch 32 Schäfchen übrig sind. Sie möchte diese in
gleich großen Gruppen aufstellen. Welche Möglichkeiten hat sie
die Schafe einzuteilen?
Level 1
einfach
2.
Zwei läutende Glocken beginnen gemeinsam. Die eine schlägt aller 8 Sekunden, die andere aller 12 Sekunden. Wann schlagen sie wieder gemeinsam?
3.
In einer Klasse befinden sich 12 Jungen und 18 Mädchen. Im Sportunterricht sollen gleich große Gruppen gebildet werden, die nur Mädchen bzw.
nur Jungen enthalten. Welches ist die größtmögliche Gruppenstärke?
4.
Rudi und Bert stapeln Kisten übereinander, Rudis Kisten sind 12cm hoch,
Berts 15cm hoch. Wann werden ihre Türme erstmals gleich hoch sein?
5.
Eine Tapetenbahn hat eine Breite von 52 cm. Wie breit kann eine Wand
sein, damit keine Tapetenbahn zerschnitten werden muss? Nenne alle
Level 2
Möglichkeiten zwischen 5 m und 7 m.
Standard
6.
Ein Betonklotz mit einer Grundfläche von 4,80m x 5,60 soll für Sprayer in
möglichst große, aber vor allem auch gleich große Abschnitte eingeteilt
werden.
a)
Wie breit ist die Fläche, die ein Sprayer dann erhält?
b) Wie viele Sprayer dürfen sich betätigen?
7.
Ein Fabrikhallenboden hat eine Länge 12m und 9,60m. Er wird mit
quadratischen Platten belegt. Wie groß dürfen die Platten
höchstens sein, damit keine zerteilt werden muss?
8.
Ein Süßwarenhändler möchte drei Packungen Bonbons (600 rote, 500 blaue
und 350 weiße) als Mischung in Tüten abfüllen und zwar so, dass jede Tüte
die gleiche Füllung aufweist und keine Bonbons übrig bleiben.
Level 4
a) Wie viele solcher Tüten kann er höchstens herstellen?
Knobeln
b) Wie viele Bonbons jeder Farbe sind dann in jeder Tüte?
c) Wie teuer wird eine Tüte der Mischung, wenn die roten Bonbons insgesamt 45€, die blauen 35€ und die weißen 20€ kosten?
Level 3
knifflig
Station 4: Primfaktorzerlegung (PFZ)
1. Welche der folgenden Zahlen sind keine Primzahlen?
1, 2, 3, 4, 5, 6, 7, 17, 19, 21, 23, 25, 27, 29, 89, 117, 143
Level 1
einfach
2. Bestimme die Primfaktor-Zerlegung von ...
a) 50
b) 18
c) 36
d) 76
e) 96
3. Welche Zahl wurde hier in ihre Primfaktoren zerlegt?
b) 33  11
a) 22
c) 22  52  7
4. Gib die Primfaktorzerlegung folgender Zahlen in Potenzschreibweise an!
a) 19
b) 333
c) 132
d) 162
e) 3 400
Level 2
Standard
5. Nenne die Zahlen, die folgende Primfaktorzerlegung haben!
a) 29
b) 32  52
6. Eine Zahl hat die Primfaktorzerlegung 2  3  5³  13²  17.
Gib 8 Teiler dieser Zahl an!
Level 3
knifflig
7.
Ist die Zahl mit der PFZ „ 2  3²  7³  11  13² “ ...
a) ... durch 77 teilbar?
b) ... durch 8 teilbar?
c) ... durch 18 teilbar?
8.
Ist die Zahl mit der Primfaktorzerlegung 2  3²  7³  11  13²
größer, kleiner oder gleich groß wie die Zahl mit der
Level 4
Primfaktor-Zerlegung 2²  3³  7²  11  13² ?
Knobeln
9. Welche Zahl hat die Primfaktorzerlegung 211  59 ?
(Gesucht ist ein „sportlicher“ Rechenweg – es geht im Kopf zu berechnen.)
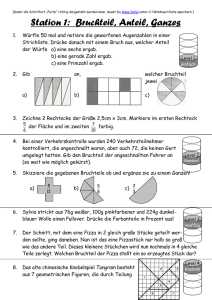
Station 5: Bruchteil, Anteil, Ganzes
1.
2.
Würfle 50 mal und notiere die geworfenen Augenzahlen in einer
Strichliste. Drücke danach mit einem Bruch aus, welcher Anteil
der Würfe a) eine sechs ergab.
b) eine gerade Zahl ergab.
c) eine Primzahl ergab.
Level 1
einfach
Gib an, welcher Bruchteil jeweils dunkel ist!
a)
b)
c)
3.
Zeichne 2 Rechtecke der Größe 2,5cm x 3cm. Markiere im ersten Rechteck
4.
Bei einer Verkehrskontrolle wurden 240 Verkehrsteilnehmer
kontrolliert, die angeschnallt waren, aber auch 72, die keinen Gurt
umgelegt hatten. Gib den Bruchteil der angeschnallten Fahrer an
(so weit wie möglich gekürzt).
5.
5
7
der Fläche und im zweiten
farbig.
10
6
Skizziere die gegebenen Bruchteile ab und ergänze sie zu einem Ganzen!
a)
6.
Level 2
Standard
5
11
b)
5
8
c)
2
3
Sylvia strickt aus 76g weißer, 100g pinkfarbener und 224g dunkelblauer Wolle einen Pullover. Drücke die Farbanteile in Prozent aus!
Level 3
knifflig
7.
Der Schnitt, mit dem eine Pizza in 2 gleich große Stücke geteilt werden sollte, ging daneben. Nun ist das eine Pizzastück nur halb so groß
wie das andere Teil. Dieses kleinere Stückchen wird nun nochmals in 4 gleiche
Teile zerlegt. Welchen Bruchteil der Pizza stellt ein so erzeugtes Stück dar?
8.
Das alte chinesische Knobelspiel Tangram besteht
aus 7 geometrischen Figuren, die durch Teilung
eines Quadrates entstanden sind. Ordne jeder
der 7 Teilflächen ihren entsprechenden Bruch zu!
(Durch Addition der Brüche kannst Du überprüfen, ob sich zusammen ein Ganzes ergibt)
Level 4
Knobeln
Station 6: Anteile von Größen
13
3
von 560m b)
von 3 600kg und c) 20% von 140min
40
7
1.
Berechne a)
2.
Gib diese Größen in der nächstkleineren Einheit an!
a)
2
h
3
b)
3
g
100
1
4
c) 2 Jahre
d)
17
km
50
e)
11
€
25
Level 1
einfach
3.
Bergmanns haben im Sommer 3kg Pilze gesammelt. Nach dem Trocknen
haben sie nun 600g Trockenpilze. Gib den Wasseranteil dieser Pilze in
Prozent an.
4.
Jedes Jahr haben etwa 4% aller Kinder einen Unfall. Mit wie vielen Unfällen
muss man dieses Jahr in Altenburg rechnen, wenn hier 5600 Kinder leben?
5.
Berechne das Ganze, wenn folgendes bekannt ist:
a)
6.
7.
7
des Weges sind 84m.
12
b) 12% des Geldes sind 360$
Level 2
Standard
5
ausgegeben. Wie viel ist noch übrig?
8
6
Bürgermeister Semmelmann sagt der Reporterin: „Nur
der Autos
25
Von 136 € wurden schon
fahren zu schnell durch den Ort. Das sind aber immer noch 246 Raser pro
Tag.“ Formuliere eine passende Frage und beantworte diese!
8.
9.
Berechne a)
9
von 20s
12
b) 25% von 12kg und c) 4% von 1,25 km
Ein Eisberg ragt 8m aus dem Wasser. Dies ist aber bekanntlich nur
zwischen
Level 3
knifflig
1
1
und
seiner Gesamthöhe. Wie groß kann demnach der
8
5
gesamte Eisberg sein?
10. Christoph sagt: „Da es im letzten Urlaub an
3
der Tage regnete, konnten
5
wir nur 6 Tage am Strand verbringen.“ Wie lang war dieser Urlaub?
7
der Seiten mit Sport. Davon
10
2
5
sind
dem Fußball gewidmet, wovon wiederum
über die erste
7
5
11. In einer Zeitschrift befassen sich
Bundesliga berichten. Welcher Bruchteil der Gesamtzeitung befasst
sich mit der ersten Fußball-Bundesliga?
Level 4
Knobeln
Station 7: Bruchumwandlung
1.
Finde durch Erweitern oder Kürzen die passende Zahl!
a)
2.
4 20

7
b)
6

7 42
c)
Kürze so weit wie möglich!
24

16
a)
120

80
16

12 3
42 6

35
e)
1

2 1000
(Denke daran: Du musst nicht alle Aufgabe lösen!)
40

200
c)
30

60
27

36
b)
16

32
d)
150

300
e)
18

30
60

100
d)
15

50
60

20
f)
125

1000
Level 1
einfach
3. Wandle die Prozentangaben in Brüche um und kürze so weit wie möglich!
a) 45%
4.
b) 60%
c) 76%
d) 50%
e) 75%
f) 170%
g) 63%
Wandle zwischen unechten Brüchen und gemischten Zahlen um!
(Tipp: Man darf Kürzen, bevor man die Zahl umwandelt. Das spart Arbeit.)
a)
14
=
8
b)
54
=
24
c)
134
=
25
114
152
5.
Kürze so weit wie möglich!
6.
Ergänze die fehlende Zahl! a)
7.
Gib diese Brüche als Prozente an!
a)
14
=
25
b)
13
=
20
c)
a)
2
5
d) 6 =
91
3
=
10

b)
e) 3
176
264
11
7
b)
21
=
44
c)
198
242
8

12 27
2
5
d) 6 =
e)
f) 44
c)
21
=
15
f)
Level 2
Standard
156
195
d)

99
12
20
14
Level 3
knifflig
24
80
8. Wandle in gemischte Zahlen um! Schreibe eventuelle Nebenrechnungen mit!
a)
9.
254
=
85
b)
65
=
24
c)
346
=
27
d)
2351
=
53
e)
Gib einen Bruch an, den man mit genau 5 verschiedenen Zahlen
kürzen kann! (Das „Kürzen“ durch 1 wird nicht mitgezählt.)
10. Nenne einen Bruch, der auf genau 4 Arten zu kürzen geht!
721
=
44
Level 4
Knobeln
Station 8: Zahlenstrahl
1.
Welche Brüche
gehören zu den
Buchstaben?
Kürze so weit
wie möglich!
Level 1
einfach
2.
Zeichne einen Zahlenstrahl (ein ganzer Schritt sind acht Kästchen), und
3 13 8
1 3
5 1 3
7
markiere darauf die Zahlen ,
, ,2 , ,2 , ,
und
!
8 8 8
4 4
8 2 2
4
3.
Markiere auf einem Zahlenstrahl, bei dem 0 und 1 zwölf Kästchen
1 3 6 19 50
11
entfernt sind, die Brüche , , ,
,
und
!
6 4 3 12 24
6
Level 2
Standard
4.
Trage auf einem Zahlenstrahl mit der Schrittweite „1 Ganzes = 8cm“
1 3 11
2 22
7
die Brüche , ,
,
,
und
ein!
2 4 8
16 32
4
5.
Notiere als echten Bruch
oder gemischte Zahl –
jeweils so weit wie möglich gekürzt.
6.
Übertrage auf Karopapier und markiere jeweils die Zahlen 1, 2 und 2 25 !
Level 3
knifflig
7.
Eine mündliche Aufgabe: Zeige jeweils, wo auf diesen Zahlenstrahlen etwa
a) der Bruch
8.
1
2
und
b) der Bruch
7
liegt!
5
9
1 11
5
,1 ,
und
sollen auf einem Zahlenstrahl dargestellt
2 8
5
4
werden. Welchen Abstand sollten zwei natürliche Zahlen haben,
damit diese Brüche dann genau auf Kästchengrenzen liegen?
Die Zahlen
(Zeichnen ist nicht verlangt!)
Level 4
Knobeln
Zusatz-Übung: Bruchrechen- Legespiel
Such Dir einen oder zwei Mitspieler. Zuerst legt Ihr Täfelchen einer Farbe
offen auf den Tisch. Mit dem Startfeld wird begonnen. Nun muss ein Bild an den
dort stehenden Bruch angelegt werden, welches diesen Bruch darstellt. Das
angelegte Täfelchen zeigt dann einen neuen Bruch und das Spiel geht weiter.
Jeder Spieler, der ein Täfelchen richtig anlegt, bekommt einen Punkt. Die beiden
letzten Täfelchen geben aber keine Punkte.